WOLFRAM SYSTEM MODELER
ControllerComparisonCompare the impact of two types of controller structures on the motion of the quadrotor |
|
Diagram
Wolfram Language
SystemModel["Aircraft.Examples.ControllerComparison"]
Information
Comparison of the different control structure
A significant challenge in quadrotor design lies in developing an effective control system. Despite the inherent nonlinearity of quadrotors, it is feasible to manage their control using simple PID-structured controllers. The only limition from linear controllers is that the rate of change of the input signals shouldn't exceed a certain threshold due to the small angle assumption which is less than 15 degree change in angle.
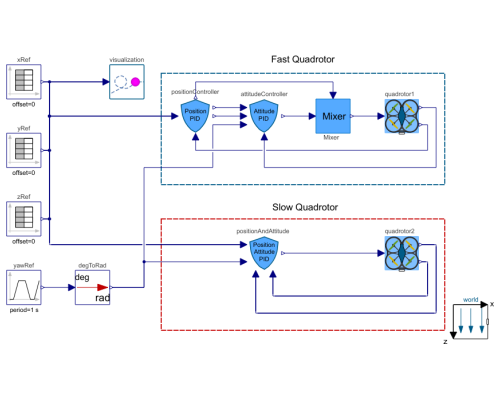
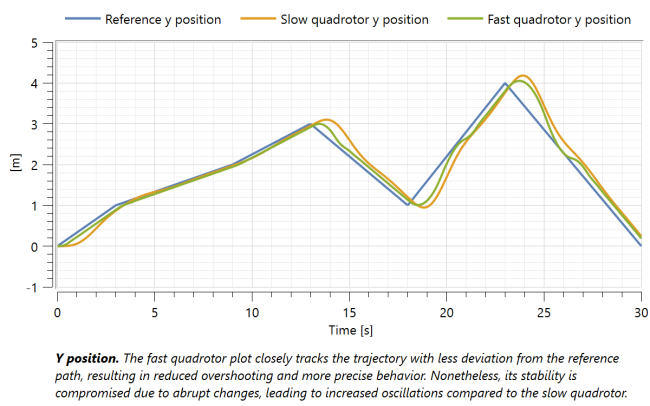
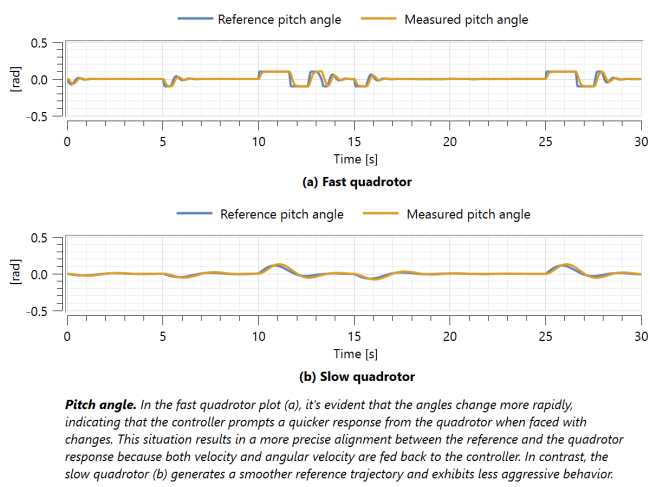
This example contrasts the behaviors of two distinct control system structures implemented on the same QuadrotorBody with identical input commands, both based on PID controllers. The inputs are the positions and the yaw angle. feeding into the controllers. In the yellow-boxed system, referred to as the "fast quadrotor," the quadrotor exhibits a quicker response. In contrast, the pink-boxed system is designated as the "stable quadrotor" due to its comparatively more stable and smoother yet slower response.
In the slow quadrotor system, control is applied over the position and angles of the quadrotor. On the other hand, the fast quadrotor's controller is more comprehensive, encompassing a position controller, attitude controller, and mixer in which velocity and the angular rate are fed back in addition to the position and angles. Consequently, the fast quadrotor's controller is designed to regulate not only the position and angles but also the velocity and angular rates of the quadcopter.
Simulation outcomes will better illustrate the difference.
Parameters (6)
| centralMass |
Value: 0.38 Type: Mass (kg) Description: Centeral mass of the quadrotor (quadrotorBody.centralMass) (quadrotor.centralMass) |
|---|---|
| xRefTable |
Value: {{0.0, 0.0}, {5, 1.0}, {10, 4.0}, {15, 2.0}, {20, 3}, {25, 4}, {30, 0}} Type: Real[:,2] (m) Description: Table matrix (time = first column; e.g., table=[0, 0; 1, 1; 2, 4]) (xRef.table) |
| yRefTable |
Value: {{0.0, 0.0}, {3, 1.0}, {9, 2.0}, {13, 3.0}, {18, 1.0}, {23, 4}, {30, 0}} Type: Real[:,2] (m) Description: Table matrix (time = first column; e.g., table=[0, 0; 1, 1; 2, 4]) (yRef.table) |
| heightRefTable |
Value: {{0.0, 0.0}, {5.0, 2.0}, {7.0, 3.0}, {13.0, 4.0}, {15.0, 2.0}, {20.0, 5.0}, {30.0, 0}} Type: Real[:,2] (m) Description: Table matrix (time = first column; e.g., table=[0, 0; 1, 1; 2, 4]) (heightRef.table) |
| yawStartTime |
Value: 0 Type: Time (s) Description: Output y = offset for time < startTime (yawRef.startTime) |
| yawAmplitude |
Value: 0 Type: Real (°) Description: Amplitude of trapezoid (yawRef.amplitude) |
Components (13)
| quadrotor2 |
Type: Quadrotor Description: Quadrotor model |
|
|---|---|---|
| positionAndAttitude |
Type: PositionAttitudePID Description: Position and attitude controller |
|
| zRef |
Type: TimeTable Description: Reference z position (height) |
|
| yRef |
Type: TimeTable Description: Reference y position |
|
| xRef |
Type: TimeTable Description: Reference x position |
|
| yawRef |
Type: Trapezoid Description: reference yaw angle |
|
| positionController |
Type: LinearPositionPID Description: Position PID controller |
|
| attitudeController |
Type: LinearAttitudePID Description: Attitude PID controller |
|
| Mixer |
Type: Mixer Description: Mixer to convert force and moment command signals to the voltage commands of each motor |
|
| quadrotor1 |
Type: Quadrotor Description: Quadrotor model |
|
| degToRad |
Type: From_deg Description: Convert yaw angle from degree to radian |
|
| world |
Type: World Description: World coordinate system used in aircraft libray |
|
| visualization |
Type: VisualizationPoint Description: Draws the reference 3D trajectory as a parametric curve |