Operator Input Forms
Operator Input Forms
Characters that are not letters, letter‐like forms, or structural elements are treated by the Wolfram Language as operators. The Wolfram Language has built‐in rules for interpreting all operators. The functions to which these operators correspond may or may not, however, have built‐in evaluation or other rules. Cases in which built‐in meanings are by default defined are indicated by ⊲ in the tables below.
Operators that construct two‐dimensional boxes—all of which have names beginning with backslash—can only be used inside \(…\). The table below gives the interpretations of these operators within ∖!∖(…∖). "Input of Boxes" gives interpretations when no \! is included.
| expr and expri | any expression |
| symb | any symbol |
| patt | any pattern object |
| string and stringi |
"cccc"
or a sequence of letters, letter
‐
like forms, and digits
|
| filename | like string, but can include additional characters described below |
| ⊲ | built‐in meanings exist |
Operator Precedence
operator form | full form | grouping | ||||||||||
| ⊲ | ||||||||||||
| ⊲ | ||||||||||||
| ⊲ | ||||||||||||
| {{e11,e12,…},{e21,e22,…},…} | ⊲ | ||||||||||
| Piecewise[{{e11,e12},{e21,e22},…}] | ⊲ | ||||||||||
| expr::string | MessageName[expr,"string"] | ⊲ | ||||||||||
| expr::string1::string2 | MessageName[expr,"string1","string2"] | ⊲ | ||||||||||
| ⊲ | ||||||||||||
| ⊲ | ||||||||||||
| ⊲ | ||||||||||||
| <<filename | Get["filename"] | ⊲ | ||||||||||
| Overscript[expr1,expr2] | ||||||||||||
| expr1\&expr2 | Overscript[expr1,expr2] | e\&(e\&e) | ||||||||||
| Underscript[expr1,expr2] | ||||||||||||
| expr1\+expr2 | Underscript[expr1,expr2] | e\+(e\+e) | ||||||||||
| Underoverscript[expr1,expr2,expr3] | ||||||||||||
| expr1\+expr2\%expr3 | Underoverscript[expr1,expr2,expr3] | |||||||||||
| expr1\&expr2\%expr3 | Underoverscript[expr1,expr3,expr2] | |||||||||||
| expr1expr2 | Subscript[expr1,expr2] | e(ee) | ||||||||||
| expr1\_expr2 | Subscript[expr1,expr2] | e\_(e\_e) | ||||||||||
| expr1\_expr2\%expr3 | Power[Subscript[expr1,expr2],expr3] | ⊲ | ||||||||||
| \!boxes |
(interpreted version of
boxes
)
| |||||||||||
| expr1?expr2 | PatternTest[expr1,expr2] | ⊲ | ||||||||||
| expr1[expr2,…] | expr1[expr2,…] | (e[e])[e] | ⊲ | |||||||||
| expr1[[expr2,…]] | Part[expr1,expr2,…] | (e[[e]])[[e]] | ⊲ | |||||||||
| expr1〚expr2,…〛 | Part[expr1,expr2,…] | (e〚e〛)〚e〛 | ⊲ | |||||||||
| expr1〚expr2〛 | Part[expr1,expr2,…] | (e〚e〛)〚e〛 | ⊲ | |||||||||
| expr1::[expr2,…] | TypeSpecifier[expr1][expr2,…] | (e::[e])::[e] | ⊲ | |||||||||
| \*expr |
(boxes constructed from
expr
)
| |||||||||||
| expr++ | Increment[expr] | ⊲ | ||||||||||
| expr-- | Decrement[expr] | ⊲ | ||||||||||
| ++expr | PreIncrement[expr] | ⊲ | ||||||||||
| --expr | PreDecrement[expr] | ⊲ | ||||||||||
| expr1@*expr2 | Composition[expr1,expr2] | e@*e@*e | ⊲ | |||||||||
| expr1/*expr2 | RightComposition[expr1,expr2] | e/*e/*e | ⊲ | |||||||||
| expr1expr2 | Application[expr1,expr2] | (ee)e | ||||||||||
| expr1@expr2 | expr1[expr2] | e@(e@e) | ⊲ | |||||||||
| expr1 expr2 | (invisible application, input as expr1 Esc@Esc expr2) | ⊲ | ||||||||||
| expr1[expr2] | ||||||||||||
| expr1~expr2~expr3 | expr2[expr1,expr3] | (e~e~e)~e~e | ⊲ | |||||||||
| expr1/@expr2 | Map[expr1,expr2] | e/@(e/@e) | ⊲ | |||||||||
| expr1//@expr2 | MapAll[expr1,expr2] | e//@(e//@e) | ⊲ | |||||||||
| expr1@@expr2 | Apply[expr1,expr2] | e@@(e@@e) | ⊲ | |||||||||
| expr1@@@expr2 | MapApply[expr1,expr2] | e@@@(e@@@e) | ⊲ | |||||||||
| expr! | Factorial[expr] | ⊲ | ||||||||||
| expr!! | Factorial2[expr] | ⊲ | ||||||||||
| expr | Conjugate[expr] | ⊲ | ||||||||||
| expr | Transpose[expr] | ⊲ | ||||||||||
| expr | ConjugateTranspose[expr] | ⊲ | ||||||||||
| expr | ConjugateTranspose[expr] | ⊲ | ||||||||||
| expr' | Derivative[1][expr] | ⊲ | ||||||||||
| expr''…' (n times) | Derivative[n][expr] | ⊲ | ||||||||||
| expr1<>expr2<>expr3 | StringJoin[expr1,expr2,expr3] | e<>e<>e | ⊲ | |||||||||
| expr1^expr2 | Power[expr1,expr2] | e^(e^e) | ⊲ | |||||||||
| expr1expr2 | Power[expr1,expr2] | e(ee) | ⊲ | |||||||||
| Power[Subscript[expr1,expr2],expr3] | ⊲ | |||||||||||
| expr1\^expr2\%expr3 | Power[Subscript[expr1,expr3],expr2] | ⊲ | ||||||||||
vertical arrow and vector operators | ||||||||||||
| Sqrt[expr] | ⊲ | |||||||||||
| \@ expr | Sqrt[expr] | \@(\@ e) | ⊲ | |||||||||
| \@ expr\%n | Power[expr,1/n] | ⊲ | ||||||||||
| expr | DifferentialD[expr] | ( e) | ⊲ | |||||||||
| ∂expr1expr2 | D[expr2,expr1] | ∂e(∂ee) | ⊲ | |||||||||
| ∇ expr | Del[expr] | ∇(∇e) | ||||||||||
| expr1expr2 | DiscreteShift[expr2,expr1] | e(ee) | ⊲ | |||||||||
| expr1expr2 | DiscreteRatio[expr2,expr1] | e(ee) | ⊲ | |||||||||
| expr1expr2 | DifferenceDelta[expr2,expr1] | e(ee) | ⊲ | |||||||||
| expr | Square[expr] | ( e) | ||||||||||
| expr1∘ expr2∘ expr3 | SmallCircle[expr1,expr2,expr3] | e∘ e∘ e | ||||||||||
| expr1⊙ expr2⊙ expr3 | CircleDot[expr1,expr2,expr3] | e ⊙ e ⊙ e | ||||||||||
| expr1**expr2**expr3 | NonCommutativeMultiply[expr1,expr2,expr3] | e**e**e | ||||||||||
| expr1expr2expr3 | Cross[expr1,expr2,expr3] | eee | ⊲ | |||||||||
| expr1.expr2.expr3 | Dot[expr1,expr2,expr3] | e.e.e | ⊲ | |||||||||
| -expr | Times[-1,expr] | ⊲ | ||||||||||
| +expr | expr | ⊲ | ||||||||||
| ±expr | PlusMinus[expr] | |||||||||||
| ∓expr | MinusPlus[expr] | |||||||||||
| expr1/expr2 | expr1(expr2)^-1 | (e/e)/e | ⊲ | |||||||||
| expr1÷expr2 | Divide[expr1,expr2] | (e÷e)÷e | ⊲ | |||||||||
| expr1\/expr2 | Divide[expr1,expr2] | (e\/e)\/e | ⊲ | |||||||||
| expr1∖expr2∖expr3 | Backslash[expr1,expr2,expr3] | e∖e∖e | ||||||||||
| expr1⋄expr2⋄expr3 | Diamond[expr1,expr2,expr3] | e⋄e⋄e | ||||||||||
| expr1⋀expr2⋀expr3 | Wedge[expr1,expr2,expr3] | e⋀e⋀e | ||||||||||
| expr1⋁expr2⋁expr3 | Vee[expr1,expr2,expr3] | e⋁e⋁e | ||||||||||
| expr1⊗expr2⊗expr3 | CircleTimes[expr1,expr2,expr3] | e⊗e⊗e | ||||||||||
| expr1·expr2·expr3 | CenterDot[expr1,expr2,expr3] | e·e·e | ||||||||||
| expr1 expr2 expr3 | Times[expr1,expr2,expr3] | e e e | ⊲ | |||||||||
| expr1*expr2*expr3 | Times[expr1,expr2,expr3] | e*e*e | ⊲ | |||||||||
| expr1×expr2×expr3 | Times[expr1,expr2,expr3] | e×e×e | ⊲ | |||||||||
| expr1⋆expr2⋆expr3 | Star[expr1,expr2,expr3] | e⋆e⋆e | ||||||||||
| Product[e4,{e1,e2,e3}] | ∏(∏ e) | ⊲ | ||||||||||
| expr1≀expr2≀expr3 | VerticalTilde[expr1,expr2,expr3] | e≀e≀e | ||||||||||
| expr1∐expr2∐expr3 | Coproduct[expr1,expr2,expr3] | e∐e∐e | ||||||||||
| expr1⌢expr2⌢expr3 | Cap[expr1,expr2,expr3] | e⌢e⌢e | ||||||||||
| expr1⌣expr2⌣expr3 | Cup[expr1,expr2,expr3] | e⌣e⌣e | ||||||||||
| expr1⊕ expr2⊕ expr3 | CirclePlus[expr1,expr2,expr3] | e⊕e⊕e | ||||||||||
| expr1⊖ expr2 | CircleMinus[expr1,expr2] | (e ⊖ e)⊖ e | ||||||||||
| ∫ expr1expr2 | Integrate[expr1,expr2] | ∫ (∫ e e) e | ⊲ | |||||||||
| Integrate[e3,{e4,e1,e2}] | ∫ (∫ e e) e | ⊲ | ||||||||||
| ∫e1∈e2e3 | Integrate[e3,e1∈e2] | ∫ (∫ e) | ⊲ | |||||||||
other integration operators | ||||||||||||
| Sum[e4,{e1,e2,e3}] | ∑(∑ e) | ⊲ | ||||||||||
| Limit[e3,e1e2] | (e) | ⊲ | ||||||||||
| MaxLimit[e3,e1e2] | (e) | ⊲ | ||||||||||
| MinLimit[e3,e1e2] | (e) | ⊲ | ||||||||||
| expr1+expr2+expr3 | Plus[expr1,expr2,expr3] | e+e+e | ⊲ | |||||||||
| expr1-expr2 | expr1+(-1expr2) | e-e-e | ⊲ | |||||||||
| expr1±expr2 | PlusMinus[expr1,expr2] | (e±e)±e | ||||||||||
| expr1∓expr2 | MinusPlus[expr1,expr2] | (e∓e)∓e | ||||||||||
| expr1⋂expr2 | Intersection[expr1,expr2] | e⋂e⋂e | ⊲ | |||||||||
other intersection operators | ||||||||||||
| expr1⋃expr2 | Union[expr1,expr2] | e⋃e⋃e | ⊲ | |||||||||
other union operators | ||||||||||||
| i;;j;;k | Span[i,j,k] | e;;e;;e | ⊲ | |||||||||
| expr1==expr2 | Equal[expr1,expr2] | e==e==e | ⊲ | |||||||||
| expr1==expr2 | Equal[expr1,expr2] | e==e==e | ⊲ | |||||||||
| expr1expr2 | Equal[expr1,expr2] | eee | ⊲ | |||||||||
| expr1!= expr2 | Unequal[expr1,expr2] | e!=e!=e | ⊲ | |||||||||
| expr1!=expr2 | Unequal[expr1,expr2] | e!=e!=e | ⊲ | |||||||||
other equality and similarity operators | ||||||||||||
| expr1>expr2 | Greater[expr1,expr2] | e>e>e | ⊲ | |||||||||
| expr1>=expr2 | GreaterEqual[expr1,expr2] | e>=e>=e | ⊲ | |||||||||
| expr1≥expr2 | GreaterEqual[expr1,expr2] | e≥e≥e | ⊲ | |||||||||
| expr1⩾expr2 | GreaterEqual[expr1,expr2] | e⩾e⩾e | ⊲ | |||||||||
| expr1<expr2 | Less[expr1,expr2] | e<e<e | ⊲ | |||||||||
| expr1<=expr2 | LessEqual[expr1,expr2] | e<=e<=e | ⊲ | |||||||||
| expr1≤expr2 | LessEqual[expr1,expr2] | e≤e≤e | ⊲ | |||||||||
| expr1⩽expr2 | LessEqual[expr1,expr2] | e⩽e⩽e | ⊲ | |||||||||
other ordering operators | ||||||||||||
| expr1expr2 | VerticalBar[expr1,expr2] | eee | ||||||||||
| expr1expr2 | NotVerticalBar[expr1,expr2] | eee | ||||||||||
| expr1∥expr2 | DoubleVerticalBar[expr1,expr2] | e∥e∥e | ||||||||||
| expr1∦expr2 | NotDoubleVerticalBar[expr1,expr2] | e∦e∦e | ||||||||||
horizontal arrow and vector operators | ||||||||||||
diagonal arrow operators | ||||||||||||
| expr1===expr2 | SameQ[expr1,expr2] | e===e===e | ⊲ | |||||||||
| expr1=!=expr2 | UnsameQ[expr1,expr2] | e=!=e=!=e | ⊲ | |||||||||
| expr1∈expr2 | Element[expr1,expr2] | e∈e∈e | ⊲ | |||||||||
| expr1∉expr2 | NotElement[expr1,expr2] | e∉e∉e | ⊲ | |||||||||
| expr1⊂expr2 | Subset[expr1,expr2] | e⊂e⊂e | ||||||||||
| expr1⊃expr2 | Superset[expr1,expr2] | e⊃e⊃e | ||||||||||
other set relation operators | ||||||||||||
| ∀expr1expr2 | ForAll[expr1,expr2] | ∀e(∀ee) | ⊲ | |||||||||
| ∃expr1expr2 | Exists[expr1,expr2] | ∃e(∃ee) | ⊲ | |||||||||
| ∄expr1expr2 | NotExists[expr1,expr2] | ∄e(∄ee) | ||||||||||
| !expr | Not[expr] | !(!e) | ⊲ | |||||||||
| ¬expr | Not[expr] | ¬(¬e) | ⊲ | |||||||||
| expr1&&expr2&&expr3 | And[expr1,expr2,expr3] | e&&e&&e | ⊲ | |||||||||
| expr1∧expr2∧expr3 | And[expr1,expr2,expr3] | e∧e∧e | ⊲ | |||||||||
| expr1⊼expr2⊼expr3 | Nand[expr1,expr2,expr3] | e⊼e⊼e | ⊲ | |||||||||
| expr1⊻expr2⊻expr3 | Xor[expr1,expr2,expr3] | e⊻e⊻e | ⊲ | |||||||||
| expr1expr2expr3 | Xnor[expr1,expr2,expr3] | eee | ⊲ | |||||||||
| expr1||expr2||expr3 | Or[expr1,expr2,expr3] | e||e||e | ⊲ | |||||||||
| expr1∨expr2∨expr3 | Or[expr1,expr2,expr3] | e∨e∨e | ⊲ | |||||||||
| expr1⊽expr2⊽expr3 | Nor[expr1,expr2,expr3] | e⊽e⊽e | ⊲ | |||||||||
| expr1⧦expr2⧦expr3 | Equivalent[expr1,expr2,expr3] | e⧦e⧦e | ⊲ | |||||||||
| expr1expr2 | Implies[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1⥰expr2 | Implies[expr1,expr2] | e⥰e⥰e | ⊲ | |||||||||
| expr1⊢expr2 | RightTee[expr1,expr2] | e⊢(e⊢e) | ||||||||||
| expr1⊨expr2 | DoubleRightTee[expr1,expr2] | e⊨(e⊨e) | ||||||||||
| expr1⊣expr2 | LeftTee[expr1,expr2] | (e⊣e)⊣e | ||||||||||
| expr1⫤expr2 | DoubleLeftTee[expr1,expr2] | (e⫤e)⫤e | ||||||||||
| expr1⊥expr2 | UpTee[expr1,expr2] | (e⊥e)⊥e | ||||||||||
| expr1⊤expr2 | DownTee[expr1,expr2] | (e⊤e)⊤e | ||||||||||
| expr1∍expr2 | SuchThat[expr1,expr2] | e∍(e∍e) | ||||||||||
| expr.. | Repeated[expr] | ⊲ | ||||||||||
| expr... | RepeatedNull[expr] | ⊲ | ||||||||||
| expr1|expr2 | Alternatives[expr1,expr2] | e|e|e | ⊲ | |||||||||
| symb:expr | Pattern[symb,expr] | ⊲ | ||||||||||
| symb:patt:expr | Optional[Pattern[symb,patt],expr] | ⊲ | ||||||||||
| patt:expr | Optional[patt,expr] | ⊲ | ||||||||||
| expr1~~expr2~~expr3 | StringExpression[expr1,expr2,expr3] | e~~e~~e | ⊲ | |||||||||
| expr1/;expr2 | Condition[expr1,expr2] | (e/;e)/;e | ⊲ | |||||||||
| expr1<->expr2 | TwoWayRule[expr1,expr2] | e<->(e<->e) | ⊲ | |||||||||
| expr1expr2 | TwoWayRule[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1expr2 | Rule[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1expr2 | Rule[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1:>expr2 | RuleDelayed[expr1,expr2] | e:>(e:>e) | ⊲ | |||||||||
| expr1 expr2 | RuleDelayed[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1/.expr2 | ReplaceAll[expr1,expr2] | (e/.e)/.e | ⊲ | |||||||||
| expr1//.expr2 | ReplaceRepeated[expr1,expr2] | (e//.e)//.e | ⊲ | |||||||||
| expr1+=expr2 | AddTo[expr1,expr2] | e+=(e+=e) | ⊲ | |||||||||
| expr1-=expr2 | SubtractFrom[expr1,expr2] | e-=(e-=e) | ⊲ | |||||||||
| expr1*=expr2 | TimesBy[expr1,expr2] | e*=(e*=e) | ⊲ | |||||||||
| expr1/=expr2 | DivideBy[expr1,expr2] | e/=(e/=e) | ⊲ | |||||||||
| expr& | Function[expr] | ⊲ | ||||||||||
| expr1∶expr2 | Colon[expr1,expr2] | e∶e∶e | ||||||||||
| expr1//=expr2 | ApplyTo[expr1,expr2] | e//=(e//=e) | ⊲ | |||||||||
| expr1//expr2 | expr2[expr1] | (e//e)//e | ||||||||||
| expr1expr2 | VerticalSeparator[expr1,expr2] | eee | ||||||||||
| expr1∴expr2 | Therefore[expr1,expr2] | e∴(e∴e) | ||||||||||
| expr1∵expr2 | Because[expr1,expr2] | (e∵e)∵e | ||||||||||
| expr1=expr2 | Set[expr1,expr2] | e=(e=e) | ⊲ | |||||||||
| expr1:=expr2 | SetDelayed[expr1,expr2] | e:=(e:=e) | ⊲ | |||||||||
| expr1^=expr2 | UpSet[expr1,expr2] | e^=(e^=e) | ⊲ | |||||||||
| expr1^:=expr2 | UpSetDelayed[expr1,expr2] | e^:=(e^:=e) | ⊲ | |||||||||
| symb/:expr1=expr2 | TagSet[symb,expr1,expr2] | ⊲ | ||||||||||
| symb/:expr1:=expr2 | TagSetDelayed[symb,expr1,expr2] | ⊲ | ||||||||||
| expr=. | Unset[expr] | ⊲ | ||||||||||
| symb/:expr=. | TagUnset[symb,expr] | ⊲ | ||||||||||
| expr1|->expr2 | Function[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr1expr2 | Function[expr1,expr2] | e(ee) | ⊲ | |||||||||
| expr>>filename | Put[expr,"filename"] | ⊲ | ||||||||||
| expr>>>filename | PutAppend[expr,"filename"] | ⊲ | ||||||||||
| expr1;expr2;expr3 | CompoundExpression[expr1,expr2,expr3] | ⊲ | ||||||||||
| expr1;expr2; | CompoundExpression[expr1,expr2,Null] | ⊲ | ||||||||||
| expr1\`expr2 | FormBox[expr2,expr1] | e\`(e\`e) | ⊲ | |||||||||
Operator input forms, in order of decreasing precedence. Operators of equal precedence are grouped together.
special input form | full form |
| # | Slot[1] |
| #n | Slot[n] |
| #string | Slot["string"] |
| ## | SlotSequence[1] |
| ##n | SlotSequence[n] |
| % | Out[ ] |
| %% | Out[-2] |
| %%…%
(
n
times)
| Out[-n] |
| %n | Out[n] |
| _ | Blank[ ] |
| _expr | Blank[expr] |
| __ | BlankSequence[ ] |
| __expr | BlankSequence[expr] |
| ___ | BlankNullSequence[ ] |
| ___expr | BlankNullSequence[expr] |
| _. | Optional[Blank[ ]] |
| symb_ | Pattern[symb,Blank[ ]] |
| symb_expr | Pattern[symb,Blank[expr]] |
| symb__ | Pattern[symb,BlankSequence[ ]] |
| symb__expr | Pattern[symb,BlankSequence[expr]] |
| symb___ | Pattern[symb,BlankNullSequence[ ]] |
| symb___expr | Pattern[symb,BlankNullSequence[expr]] |
| symb_. | Optional[Pattern[symb,Blank[ ]]] |
| _ :expr | Optional[Blank[],expr] |
| symb_:expr | Optional[Pattern[symb,Blank[]],expr] |
| _head :expr | Optional[Blank[head],expr] |
| symb_head:expr | Optional[Pattern[symb,Blank[head]],expr] |
Special Characters
Special characters that appear in operators usually have names that correspond to the names of the functions they represent. Thus the character  has the name ⊕ and yields the function CirclePlus. Exceptions are ⩾, ⩽ and ⥰.
has the name ⊕ and yields the function CirclePlus. Exceptions are ⩾, ⩽ and ⥰.
"Listing of Named Characters" gives a complete listing of special characters that appear in operators.
|
|
|
|
Precedence and the Ordering of Input Forms
The tables of input forms are arranged in decreasing order of precedence. Input forms in the same box have the same precedence. Each page in the table begins a new box. As discussed in "Special Ways to Input Expressions", precedence determines how the Wolfram Language groups terms in input expressions. The general rule is that if  has higher precedence than
has higher precedence than  , then
, then 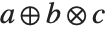 is interpreted as
is interpreted as 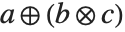 , and
, and 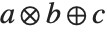 is interpreted as
is interpreted as 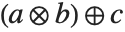 .
.
Grouping of Input Forms
The third columns in the tables show how multiple occurrences of a single input form, or of several input forms with the same precedence, are grouped. For example, a/b/c is grouped as (a/b)/c ("left associative"), while a^b^c is grouped as a^(b^c) ("right associative"). No grouping is needed in an expression like a+b+c, since Plus is fully associative, as represented by the attribute Flat.
Precedence of Integration Operators
Forms such as 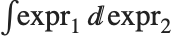 involve two operators: \[Integral] and \[DifferentialD]. The former has a precedence just above
involve two operators: \[Integral] and \[DifferentialD]. The former has a precedence just above 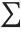 , while the latter has one just below Power. The precedence of
, while the latter has one just below Power. The precedence of 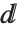 determines when
determines when  needs to be parenthesized, while the precedence of
needs to be parenthesized, while the precedence of 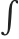 determines when
determines when  needs to be parenthesized. Note that the form
needs to be parenthesized. Note that the form  does not involve
does not involve 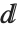 , and therefore
, and therefore 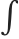 behaves like a normal prefix operator in this case.
behaves like a normal prefix operator in this case.
See "Two-Dimensional Input Forms" for two‐dimensional input forms associated with integration operators.
Spaces and Multiplication
Spaces in the Wolfram Language denote multiplication, just as they do in standard mathematical notation. In addition, the Wolfram Language takes complete expressions that are adjacent, not necessarily separated by spaces, to be multiplied together.
| ■ x y z ⟶ x*y*z |
| ■ 2x ⟶ 2*x |
| ■ 2(x+1) ⟶ 2*(x+1) |
| ■ c(x+1) ⟶ c*(x+1) |
| ■ (x+1)(y+2) ⟶ (x+1)*(y+2) |
| ■ x! y ⟶ x!*y |
| ■ x!y ⟶ x!*y |
An expression like x!y could potentially mean either (x!)*y or x*(!y). The first interpretation is chosen because Factorial has higher precedence than Not.
Spaces within single input forms are ignored. Thus, for example, a + b is equivalent to a+b. You will often want to insert spaces around lower precedence operators to improve readability.
You can give a "coefficient" for a symbol by preceding it with any sequence of digits. When you use numbers in bases larger than 10, the digits can include letters. (In bases other than 10, there must be a space between the end of the coefficient and the beginning of the symbol name.)
■ x^2y, like x^2 y, means (x^2) y |
■ x/2y, like x/2 y, means (x/2) y |
■ xy is a single symbol, not x*y |
Spaces to Avoid
You should avoid inserting any spaces between the different characters in composite operators such as /., =., and >=. Although in some cases such spaces are allowed, they are liable to lead to confusion.
Another case where spaces must be avoided is between the characters of the pattern object x_. If you type x_, the Wolfram Language will interpret this as x*_, rather than the single named pattern object x_.
Spacing Characters
Relational Operators
Relational operators can be mixed. An expression like a>b>=c is converted to Inequality[a,Greater,b,GreaterEqual,c], which effectively evaluates as (a>b)&&(b>=c). (The reason for the intermediate Inequality form is that it prevents objects from being evaluated twice when input like a>b>=c is processed.)
File Names
Any file name can be given in quotes after <<, >>, and >>>. File names can also be given without quotes if they contain only alphanumeric characters and the characters `, /, ., ∖, !, -, _, :, $, *, ~, and ?, together with matched pairs of square brackets enclosing any characters other than spaces, tabs, and newlines. Note that file names given without quotes can be followed only by spaces, tabs, or newlines, or by the characters ), ], or }, as well as semicolons and commas.
Related Guides
-
▪
- Syntax