CentralFeature
CentralFeature[{x1,x2,…}]
给出元素 ![]() 的中心要素.
的中心要素.
CentralFeature[{x1v1,x2v2,…}]
给出对应于中心要素 ![]() 的 vi.
的 vi.
CentralFeature[data]
给出不同格式的 data 的中心要素.
更多信息和选项


- CentralFeature 是一种位置度量. 它给出数据中距其他点的的距离的总和最小的那个点.
- CentralFeature 找出使得距离和
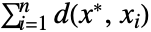 (没有加权) 最小的元素
(没有加权) 最小的元素 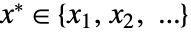 ,有加权的情况下,为
,有加权的情况下,为 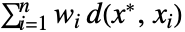 .
. - 数据 data 的格式和解释如下所示:
-
{data1,data2,…} 不同格式的数据的列表,包括数值、地理空间、文字、可视图形、日期、时间,以及上述类型的组合 {data1,data2,…}{v1,v2,…} 带有索引 {v1,v2,…} 的数据 {data1,data2,…}Automatic vi 取连续整数 i GeoPosition[…] 测地位置数组 WeightedData[…] 带有权重的数据 - 可以给出下列选项:
-
DistanceFunction Automatic 要使用的距离度量 - DistanceFunction 的设置可以为任意距离、相异度函数或定义两点之间的距离的函数 f.
- 缺省情况下,下列距离函数被用于不同类型的元素:
-
EuclideanDistance 数值型数据 ImageDistance 图像 JaccardDissimilarity 布尔数据 EditDistance 文字和标称序列 Abs[DateDifference[#1,#2]]& 日期和时间 ColorDistance 颜色 GeoDistance 地理空间数据 Boole[SameQ[#1,#2]]& 标称数据 HammingDistance 标称向量数据 WarpingDistance 数值序列 - 当选项 DistanceFunction 设为 Automatic 时,先用 ConformImages 对所有图像进行一致化 (conform) 处理.
- 缺省情况下,如果数据元素是混合类型的向量,对每个类型单独计算距离,再用 Norm 组合在一起.

范例
打开所有单元关闭所有单元范围 (9)
可对 WeightedData 求中心要素:
选项 (2)
DistanceFunction (2)
应用 (4)
极值对 Mean 有很大的影响:
画出城市的位置(灰色),未加权的中心要素(红色)和加权的中心要素(黑色):
根据 TravelDistance 算出的八个城市的中心要素:
根据 TravelDistance 算出的从中心要素到其他城市的距离的和:
属性和关系 (5)
CentralFeature 是一个多变量位置度量:
Mean 也是一种位置度量:
CentralFeature 找出最小化距离和的数据点:
对于单变量数据,当数据长度是奇数时, CentralFeature 与 Median 相同:
CentralFeature 找出数据中使得到其他数据点的距离之和最小化的元素:
SpatialMedian 找出域中最小化距离和的点:
相对于 CentralFeature 的距离和要大于或等于相对于 SpatialMedian 的距离和:
找出 GraphCenter:
用 GraphDistance 指定每对顶点间的距离:
用 CentralFeature 找出中心:
可能存在的问题 (1)
对于非加权的双元素列表,CentralFeature 返回第一个元素:
文本
Wolfram Research (2017),CentralFeature,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CentralFeature.html.
CMS
Wolfram 语言. 2017. "CentralFeature." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CentralFeature.html.
APA
Wolfram 语言. (2017). CentralFeature. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CentralFeature.html 年