CentralFeature[{x1,x2,…}]
gives the central feature of the elements ![]() .
.
CentralFeature[{x1v1,x2v2,…}]
gives the vi corresponding to the central feature ![]() .
.
CentralFeature[data]
gives the central feature for several different forms of data.


CentralFeature
CentralFeature[{x1,x2,…}]
gives the central feature of the elements ![]() .
.
CentralFeature[{x1v1,x2v2,…}]
gives the vi corresponding to the central feature ![]() .
.
CentralFeature[data]
gives the central feature for several different forms of data.
Details and Options


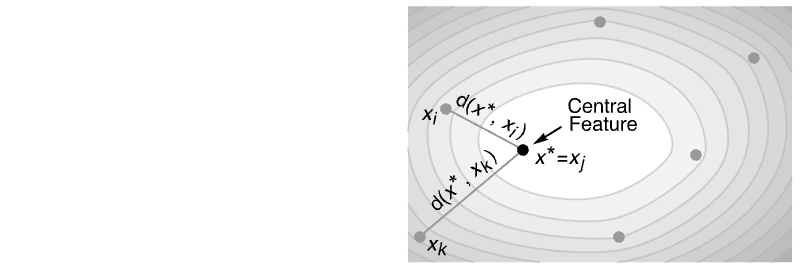
- CentralFeature is a location measure. It gives a point in the data with the minimum total distance to every other point.
- CentralFeature finds the element
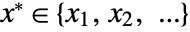 that minimizes the sum of distances
that minimizes the sum of distances 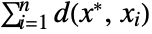 for the unweighted case and
for the unweighted case and 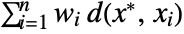 for the weighted case.
for the weighted case. - The data data has the following forms and interpretations:
-
{data1,data2,…} list of data of different formats including numerical, geospatial, textual, visual, dates and times, as well as combinations of these {data1,data2,…}{v1,v2,…} data with indices {v1,v2,…} {data1,data2,…}Automatic take the vi to be successive integers i GeoPosition[…] array of geodetic positions WeightedData[…] data with weights - The following option can be given:
-
DistanceFunction Automatic the distance metric to use - The setting for DistanceFunction can be any distance or dissimilarity function or a function f defining a distance between two points.
- By default, the following distance functions are used for different types of elements:
-
EuclideanDistance numeric data ImageDistance images JaccardDissimilarity Boolean data EditDistance text and nominal sequences Abs[DateDifference[#1,#2]]& dates and times ColorDistance colors GeoDistance geospatial data Boole[SameQ[#1,#2]]& nominal data HammingDistance nominal vector data WarpingDistance numerical sequences - All images are first conformed using ConformImages when the option DistanceFunction is Automatic.
- By default, when data elements are mixed-type vectors, distances are computed independently for each type and combined using Norm.
Examples
open all close allBasic Examples (2)
Scope (9)
Same inputs with different output formats:
Central feature works with WeightedData:
Central feature of a large array:
Find the central feature of data involving quantities:
Find the central feature of a list of images:
Compute the central feature of strings:
Compute the central feature of Boolean vectors:
Options (2)
DistanceFunction (2)
By default, Euclidean distance is used:
The ChessboardDistance only takes into account the dimension with the largest separation:
The DistanceFunction can be given as a symbol:
Applications (4)
Obtain a robust estimate of multivariate location when outliers are present:
Extreme values have a large influence on the Mean:
Sample points from a convex polygon:
Estimate the center of the polygon by computing the central feature of random points:
Find the central feature of California, based on the location of cities:
Find the central feature of California, based on the location of cities weighted by population:
Draw the cities' locations (gray), unweighted central feature (red) and weighted central feature (black):
The top eight largest cities in Ohio:
The central feature of the eight cities based on TravelDistance:
The sum of distances from the central feature to the other cities, based on TravelDistance:
Draw the cities' locations (gray) and the central feature (red):
Properties & Relations (5)
CentralFeature is a multivariate location measure:
Mean is also a location measure:
Visualize the data points with central feature and mean:
CentralFeature finds a point belonging to the data that minimizes the sum of distances:
Compute the central feature directly from the definition:
Visualize the sum of distances function together with the data points:
CentralFeature is the same as Median with univariate data when the data length is odd:
CentralFeature finds an element in the data that minimizes the sum of distances to other data points:
SpatialMedian finds a point in the domain that minimizes the sum of distances:
The sum of distances with respect to CentralFeature is greater than or equal to the one with respect to SpatialMedian:
Create a random graph with edge weights sampled uniformly between 0 and 1:
Locate the GraphCenter:
Specify the distance between each pair of vertices using GraphDistance:
Locate the center using CentralFeature:
Possible Issues (1)
CentralFeature of a non-weighted, two-element list returns the first element:
For weighted two-element lists, it chooses the element with the highest weight, which trivially minimizes ![]() :
:
History
Text
Wolfram Research (2017), CentralFeature, Wolfram Language function, https://reference.wolfram.com/language/ref/CentralFeature.html.
CMS
Wolfram Language. 2017. "CentralFeature." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CentralFeature.html.
APA
Wolfram Language. (2017). CentralFeature. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralFeature.html
BibTeX
@misc{reference.wolfram_2025_centralfeature, author="Wolfram Research", title="{CentralFeature}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/CentralFeature.html}", note=[Accessed: 15-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_centralfeature, organization={Wolfram Research}, title={CentralFeature}, year={2017}, url={https://reference.wolfram.com/language/ref/CentralFeature.html}, note=[Accessed: 15-December-2025]}