CopulaDistribution
CopulaDistribution[ker,{dist1,dist2,…}]
カーネル分布 ker,周辺分布 dist1, dist2, … のコピュラ分布を表す.
詳細


- 累積分布関数は
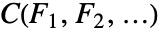 で与えられる.ただし,
で与えられる.ただし,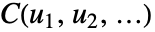 はカーネル ker の累積分布関数,
はカーネル ker の累積分布関数,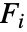 は distiの累積分布関数である.
は distiの累積分布関数である. - 周辺分布 distiは任意の一変量分布でよい.
- 次のカーネル ker を使うことができる.
-
"Product" 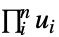
独立分布 "Maximal" 
Frechét–Hoeffding上界 "Minimal" 
Frechét–Hoeffding下界 {"Frank",α} 
Frankコピュラ {"Clayton",c} 
Clayton–Paretoコピュラ {"GumbelHougaard",α} 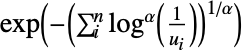
Gumbel–Hougaardコピュラ {"FGM",α} 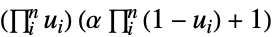
Farlie–Gumbel–Morgensternコピュラ {"AMH",α} 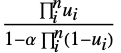
Ali–Mikhail–Haqコピュラ {"Binormal",ρ} 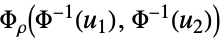
相関が 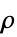 の二変量ガウス分布
の二変量ガウス分布{"Multinormal",Σ} 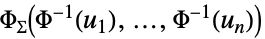
共分散が 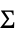 の多変量ガウス分布
の多変量ガウス分布{"MultivariateT",Σ,ν} 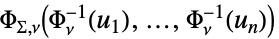
尺度行列 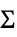 ,自由度
,自由度 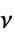 の多変量
の多変量 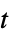 分布
分布 - "Frank"の場合,
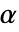 は二次元の任意の正の数,あるいは,二次元より上の次元では,特定の定数
は二次元の任意の正の数,あるいは,二次元より上の次元では,特定の定数 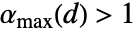 以下の任意の正の数でよい.
以下の任意の正の数でよい. - "Clayton"の場合は,
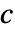 は任意の正の数でよい.
は任意の正の数でよい. - "GumbelHougaard"の場合は,
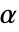 は1以上の任意の実数でよい.
は1以上の任意の実数でよい. - "FGM"と"AMH"の場合は,
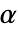 は
は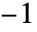 から
から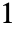 までの任意の実数でよい.
までの任意の実数でよい. - "Binormal","Multinormal","MultivariateT"の母数はそれぞれBinormalDistribution,MultinormalDistribution,MultivariateTDistributionのものと同じである.
- CopulaDistributionは,Mean,PDF,RandomVariate等の関数とともに使うことができる.
予備知識
- CopulaDistribution[ker,{dist1,dist2,…,distn}]は,第
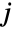 周辺分布(MarginalDistribution)が厳密に distjであり,distjに従う確率変量の累積分布関数が一様分布(UniformDistribution)に従う
周辺分布(MarginalDistribution)が厳密に distjであり,distjに従う確率変量の累積分布関数が一様分布(UniformDistribution)に従う 多変量統計分布を表す.一般的なコピュラ分布CopulaDistribution[ker,{dist1,dist2,…,distn}]については,Yj=TransformedDistribution[Fj[x],xdistj]の確率密度関数(PDF)は,Fj[x]が distjの累積分布関数である場合は常にUniformDistribution[]に等しい.コピュラ分布はすべて上記の特性を有するが,特定のコピュラ分布の特徴と動作はそのカーネル ker と周辺分布 dist1,dist2,…,distnに依存する.
多変量統計分布を表す.一般的なコピュラ分布CopulaDistribution[ker,{dist1,dist2,…,distn}]については,Yj=TransformedDistribution[Fj[x],xdistj]の確率密度関数(PDF)は,Fj[x]が distjの累積分布関数である場合は常にUniformDistribution[]に等しい.コピュラ分布はすべて上記の特性を有するが,特定のコピュラ分布の特徴と動作はそのカーネル ker と周辺分布 dist1,dist2,…,distnに依存する. - コピュラ分布は,実際のところ,変数間の依存関係を説明するツールであり,この文脈では,ker を変えることでさまざまな依存度を調べることができる(例:{"FGM",α}は変数間の弱い依存関係の分析ができ,"Product"は独立変数の分析ができる).コピュラ分布のパラメータ化に使える定義済みのカーネル ker は11個あり,独立・従属カーネル("Product","Maximal","Minimal"),アルキメデスカーネル({"Frank",α},ただし,
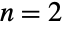 のときは
のときは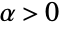 で
で 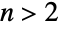 のときは
のときは 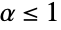 ,
,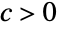 についての{"Clayton",c},
についての{"Clayton",c},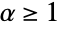 についての {"GumbelHougaard",α},
についての {"GumbelHougaard",α},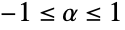 についての{"AMH",α}),分布派生カーネル(BinormalDistributionにおけるような ρ についての{"Binormal",ρ},MultinormalDistributionにおけるような Σ についての{"Multinormal",Σ},MultivariateTDistributionにおけるような Σ および ν についての{"MultivariateT",Σ,ν},非結合カーネル(
についての{"AMH",α}),分布派生カーネル(BinormalDistributionにおけるような ρ についての{"Binormal",ρ},MultinormalDistributionにおけるような Σ についての{"Multinormal",Σ},MultivariateTDistributionにおけるような Σ および ν についての{"MultivariateT",Σ,ν},非結合カーネル(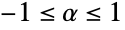 について{"FGM",α})の4つのグループに分けることができる.メンバーは定性的あるいは理論的に同じような特性を共有する.
について{"FGM",α})の4つのグループに分けることができる.メンバーは定性的あるいは理論的に同じような特性を共有する. - Sklarの定理は,関係
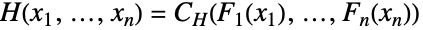 を介して任意の結合分布
を介して任意の結合分布 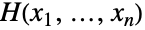 とその一変量周辺分布
とその一変量周辺分布 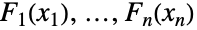 を「カップル」にするコピュラ
を「カップル」にするコピュラ 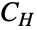 が存在し,したがって,コピュラ分布が多変量統計のいたるところに存在することを証明した.コピュラ分布は1940年代にまで遡ることができるが,今日使用されている用語と構造の多くは1950年代から1960年代にかけて開発されたものである.コピュラは,その萌芽期より,信頼性理論,気象学,待ち行列理論を含むさまざまな分野における現象のモデル化に使われている.また,生存分析における生存コピュラや金融工学におけるパニックコピュラのように,各分野のツールとなるように特別な目的を持ったコピュラおよびカーネルも開発されている.コピュラ分布は,モンテカルロ理論や応用数学でも,他とは無関係の理論的興味を集めている.
が存在し,したがって,コピュラ分布が多変量統計のいたるところに存在することを証明した.コピュラ分布は1940年代にまで遡ることができるが,今日使用されている用語と構造の多くは1950年代から1960年代にかけて開発されたものである.コピュラは,その萌芽期より,信頼性理論,気象学,待ち行列理論を含むさまざまな分野における現象のモデル化に使われている.また,生存分析における生存コピュラや金融工学におけるパニックコピュラのように,各分野のツールとなるように特別な目的を持ったコピュラおよびカーネルも開発されている.コピュラ分布は,モンテカルロ理論や応用数学でも,他とは無関係の理論的興味を集めている. - CopulaDistribution[ker,{dist1,…,distn}]と他のさまざまな分布の間には,パラメータ ker と distjによって数多くの関係がある.すべての分布 distjについて,CopulaDistribution["Product",{dist1,…,distn}]はProductDistribution[dist1,…,distn]に等しく,2つのNormalDistributionの積コピュラはBinormalDistributionである.さらに,積コピュラは,CopulaDistribution["Product",{dist1,…,distn}]の確率密度分布が,すべての分布 distjについて,CopulaDistribution[{"Binormal",0},{dist1,…,distn}]のそれと厳密に等しいという意味で,ゼロ相関の二項正規コピュラと等しい.分布由来カーネルの中で,NormalDistributionに従う周辺分布のある二項正規コピュラとStudentTDistributionに従う周辺分布のある多変量
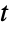 コピュラは,それぞれBinormalDistributionとMultivariateTDistributionに等しい.また,アルキメデスコピュラとさまざまな分布の間には定性的に同じような関係が数限りなく存在する.
コピュラは,それぞれBinormalDistributionとMultivariateTDistributionに等しい.また,アルキメデスコピュラとさまざまな分布の間には定性的に同じような関係が数限りなく存在する.
例題
すべて開くすべて閉じるスコープ (32)
基本的な用法 (6)
コピュラカーネル (11)
パラメトリック分布 (4)
ノンパラメトリック分布 (3)
SmoothKernelDistributionのコピュラ分布を定義する:
EmpiricalDistributionのコピュラ分布を定義する:
HistogramDistributionのコピュラ分布を定義する:
派生分布 (8)
TruncatedDistributionを周辺分布としてコピュラ分布を定義する:
CensoredDistributionを周辺分布としてコピュラ分布を定義する:
MixtureDistributionを周辺分布としてコピュラ分布を定義する:
ParameterMixtureDistributionを周辺分布としてコピュラ分布を定義する:
OrderDistributionを周辺分布としてコピュラ分布を定義する:
TransformedDistributionを周辺分布としてコピュラ分布を定義する:
MarginalDistributionを周辺分布としてコピュラ分布を定義する:
QuantityDistributionが周辺分布のコピュラ分布を評価するとQuantityDistributionになる:
アプリケーション (6)
4つの部品からなるシステムがある.それぞれの部品の寿命は1時間あたり![]() を母数として指数的に分布している.故障までの時間に対する依存度はα1/3のFarlie–Gumbel–Morgensternコピュラ分布でモデル化される.500時間経ってもどの部品も故障していない確率を求める:
を母数として指数的に分布している.故障までの時間に対する依存度はα1/3のFarlie–Gumbel–Morgensternコピュラ分布でモデル化される.500時間経ってもどの部品も故障していない確率を求める:
2つの資産の値がそれぞれドリフト ![]() と
と ![]() ,ボラティリティ
,ボラティリティ ![]() と
と ![]() で幾何ブラウン運動に従うと仮定する.両方の初期値を1と仮定して,時間
で幾何ブラウン運動に従うと仮定する.両方の初期値を1と仮定して,時間 ![]() における両方の資産の連結累積分布関数の境界を求める:
における両方の資産の連結累積分布関数の境界を求める:
2つの会社にそれぞれ ![]() と
と ![]() の負債があり,双方とも初期資産が1であったと仮定する.資産の値がそれぞれドリフト
の負債があり,双方とも初期資産が1であったと仮定する.資産の値がそれぞれドリフト ![]() と
と ![]() ,ボラティリティ
,ボラティリティ ![]() と
と ![]() で幾何ブラウン運動に従うと仮定する.Frankコピュラを仮定して時間
で幾何ブラウン運動に従うと仮定する.Frankコピュラを仮定して時間 ![]() におけるデフォルトの連結確率を求める:
におけるデフォルトの連結確率を求める:
コーシーコピュラは自由度1の多変量スチューデント ![]() コピュラである:
コピュラである:
母数の異なる値についてGumbel–Hougaardコピュラを定義する:
特性と関係 (5)
周辺分布が正規分布の二変量正規コピュラはBinormalDistributionである:
周辺分布がスチューデント ![]() ’分布の多変量
’分布の多変量 ![]() コピュラはMultivariateTDistributionである:
コピュラはMultivariateTDistributionである:
コピュラのMarginalDistributionは成分分布を返す:
考えられる問題 (1)
テキスト
Wolfram Research (2010), CopulaDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/CopulaDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "CopulaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/CopulaDistribution.html.
APA
Wolfram Language. (2010). CopulaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CopulaDistribution.html