CopulaDistribution

CopulaDistribution[ker,{dist1,dist2,…}]

表示核分布为 ker、边缘分布为 dist1、dist2、… 的 Copula 分布.

更多信息

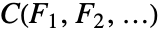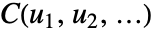  • 累积分布函数由 给出，其中 为核 ker 的累积分布函数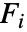， 为 disti 的累积分布函数.
  • 边际分布 disti 可为任一单变量分布.
  • 可以使用下列核 ker：
  • "Product"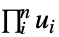独立分布
    "Maximal"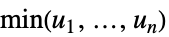Frechét–Hoeffding 上界
    "Minimal"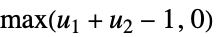Frechét–Hoeffding 下界
    {"Frank",α}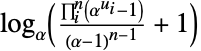Frank copula
    {"Clayton",c}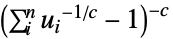Clayton–Pareto copula
    {"GumbelHougaard",α}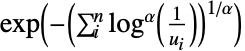Gumbel–Hougaard copula
    {"FGM",α}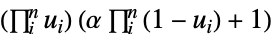Farlie–Gumbel–Morgenstern copula
    {"AMH",α}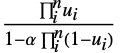Ali–Mikhail–Haq copula
    {"Binormal",ρ}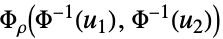相关系数为 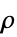的二元高斯分布
    {"Multinormal",Σ}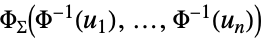协方差为 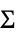的多变量高斯分布
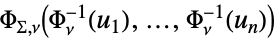
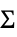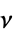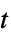    {"MultivariateT",Σ,ν}缩放矩阵为 、自由度为 的多变量 分布
  • 对于 "Frank"，二维情况下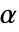， 可以是任何正数，高于二维的情况下，则可以是任何小于或等于某个常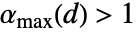数 的正数.
  • 对于 "Clayton"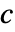， 可以是任意正数.
  • 对于 "GumbelHougaard"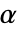， 可以是任意大于或者等于 1 的实数.
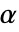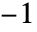  • 对于 "FGM" 和 "AMH"， 可以是任意 和 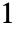之间的实数.
  • "Binormal"、"Multinormal" 和 "MultivariateT" 的参数分别与 BinormalDistribution、MultinormalDistribution 和 MultivariateTDistribution 的参数相同.
  • CopulaDistribution 可与 Mean、PDF 以及 RandomVariate 等函数联合使用.

背景

  • CopulaDistribution[ker,{dist1,dist2,…,distn}] 表示一个第 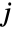个边际分布（MarginalDistribution）为 distj 的多变量统计分布，并且 distj 分布随机变量的 CDF 遵循均匀分布（UniformDistribution）. 对于更一般的 copula 分布 CopulaDistribution[ker,{dist1,dist2,…,distn}] 而言，当 Fj[x] 是 distj 的 CDF 时 Yj=TransformedDistribution[Fj[x],xdistj] 的概率密度函数（PDF）等价于 UniformDistribution[]. 尽管所有 copula 分布都有上述属性，但一个具体 copula 分布的特性和行为取决于其核 ker 及其边缘 dist1,dist2,…,distn.
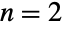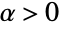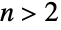  • 事实上，copula 是描述变量之间的依赖性的工具，在这里，改变 ker 可以对不同依存度进行研究（比如 {"FGM",α} 能最好地对弱变量关联建模，而 "Product" 允许对独立变量的分析）. 有 11 个可用于参数化一个 copula 分布的预定义的核 ker. 这 11 个核可以被大致分成四组，包括独立-依赖核（"Product"、 "Maximal" 和 "Minimal"）；阿基米德核（{"Frank",α}，其中 时 ， 时 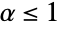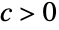， 时的 {"Clayton",c}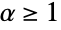， 时的 {"GumbelHougaard",α} 和 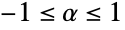时的 {"AMH",α}）；分布衍生核（{"Binormal",ρ} 其中 ρ 如 BinormalDistribution 中的， {"Multinormal",Σ} 其中 Σ 如 MultinormalDistribution 中的、 ν 如 MultivariateTDistribution 中的）；和非关联核（{"FGM",α} 其中 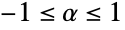），其成员有相似的定性的或理论上的属性.
  • Sklar 理论证明了存在一个 copula 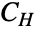，它通过关联 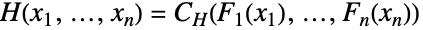将任意联合分布 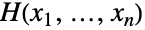和其单变量边缘 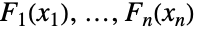结合并由此证明 copula 分布在多变量统计中是普遍存在的. 尽管今天使用的很多术语和装置是在 1950 到 1960 年代发展起来的，copula 分布可以追溯至 1940 年代. 起初，copula 被用于对可靠性理论、气象学和排队论中的现象建模，后来开发出特殊定义的 copula 和核作为生存分析（通过survival copulas）和数学金融（通过 panic copulas）等领域中的工具. Copula 分布在蒙特卡罗理论和应用数学中也有独立的理论兴趣.
  • 根据参数 ker 和 distj，CopulaDistribution[ker,{dist1,…,distn}] 和各种其他分布之间存在很多关系. 对所有分布 distj， CopulaDistribution["Product",{dist1,…,distn}] 等价于 ProductDistribution[dist1,…,distn]，同样的 NormalDistribution 的两个实例的积 copula 是 BinormalDistribution. 另外，对所有的 distj 分布， CopulaDistribution["Product",{dist1,…,distn}] 的 PDF 与 CopulaDistribution[{"Binormal",0},{dist1,…,distn}] 的 PDF 是一样的， 就此意义而言积 copula 等价于有零关联的双正态. 在分布衍生核中，有 NormalDistribution 边缘的双正态 copula 等价于有 StudentTDistribution 边缘的多变量 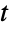-copula，相应的，无数定性的类似关系存在于阿基米德 copula 和各种分布之间.

范例

打开所有单元关闭所有单元

基本范例  (3)

定义一个乘积 copula：

定义一个 Farlie–Gumbel–Morgenstern copula：

定义一个三维最大 copula：

范围  (32)

基本用途  (6)

利用两个正态分布定义一个乘积 Copula：

概率密度函数：

累积分布函数：

利用两个均匀分布定义一个 Frank copula：

生成随机向量：

比较均值和方差：

利用贝塔分布定义一个 FGM copula：

矩和矩母函数：

定义具有离散分量的最大 copula：

概率密度函数：

计算概率和期望值：

利用泊松分布定义一个最小 copula：

概率密度函数：

按照分量计算统计属性：

估计分布参数：

Copula 核  (11)

一个乘积 copula：

概率密度函数：

累积分布函数：

一个最大 copula：

累积分布函数：

一个最小 copula：

累积分布函数：

一个 Frank copula：

概率密度函数：

累积分布函数：

一个 Clayton copula：

概率密度函数：

累积分布函数：

一个 Gumbel–Hougaard copula：

概率密度函数：

累积分布函数：

一个 Farlie–Gordon–Morgenstern copula：

概率密度函数：

累积分布函数：

一个 Ali–Mikhail–Haque copula：

概率密度函数：

累积分布函数：

一个二元正态 copula：

概率密度函数：

一个多元正态 copula：

概率密度函数：

一个多元学生 copula：

概率密度函数：

参数分布  (4)

利用贝塔分布作为边缘分布定义一个最小 copula：

累积分布函数：

生存函数：

利用不同的连续边缘分布定义一个最大 copula：

累积分布函数：

均值和方差：

偏度和峰度：

利用泊松边缘分布定义一个 copula：

概率密度函数：

风险函数：

利用负二项分布作为边缘分布定义一个 copula：

概率密度函数：

生成随机数：

非参数分布  (3)

利用 SmoothKernelDistribution 定义一个 copula：

概率密度函数：

均值和方差：

利用 EmpiricalDistribution 定义一个 copula：

概率密度函数：

利用 HistogramDistribution 定义一个 copula：

绘制概率密度函数的图线：

累积分布函数：

导出分布  (8)

利用 TruncatedDistribution 作为边缘分布定义一个 copula 分布：

概率密度函数：

利用 CensoredDistribution 作为一个边缘分布定义一个 copula 分布：

概率密度函数：

均值和方差：

利用 MixtureDistribution 作为一个边缘分布定义一个 copula：

概率密度函数：

累积分布函数：

利用 ParameterMixtureDistribution 作为一个边缘分布定义一个 copula：

概率密度函数：

风险函数：

利用 OrderDistribution 作为一个边缘分布定义一个 copula：

概率密度函数：

累积分布函数：

利用 TransformedDistribution 作为一个边缘分布定义一个 copula：

概率密度函数：

均值和方差：

偏度和峰度：

利用 MarginalDistribution 作为一个边缘分布定义一个 copula：

概率密度函数：

有 QuantityDistribution 边缘的 copula 估值到 QuantityDistribution：

均值和方差：

应用  (6)

一个系统由四个组件组成，每个组件的生命期服从参数为 的指数分布. 与失效时间的依赖关系根据参数为 α1/3 的 Farlie–Gumbel–Morgenstern copula建模. 求没有任何组件在 500 小时前失效的概率：

求在 1000 个小时后有一个组件失效的概率：

假定两个资产的值服从漂移率为 和 ，波动率为 和 的几何布朗运动. 假定两个资产的初始值都为 1，求在时间 时，这两个资产的联合累积分布函数的边界值：

下界：

上界：

假定下面的值比较累积分布函数的图线：

两家公司有债务 和 ，初始资产都是 1. 假定资产值服从漂移率为 和 ，波动率为 和 的几何布朗运动. 假定一个 Frank copula，求在时间 时默认的联合概率：

默认的概率依赖于 α：

极限值：

一个柯西 copula 是自由度为 1 的多变量学生 copula：

概率密度函数：

利用一个散点图，将密度可视化：

对于不同的参数值，定义一个 Gumbel–Hougaard copula：

显示参数值如何影响值之间的依赖关系：

Gumbel 双变量逻辑斯蒂分布是具有逻辑斯蒂边际分布的 AMH Copula：

可视化其概率密度函数：

累积分布函数具有单变量逻辑斯蒂分布的 CDF 结构：

属性和关系  (5)

两个正态分布的乘积 copula 分布是一个二元正态分布：

乘积 copula 等价于相关度为零的二元正态 copula：

具有正态边缘分布的二项 copula 是一个 BinormalDistribution：

具有学生 边缘分布的多元 copula 是一个 MultivariateTDistribution：

一个 copula 的 MarginalDistribution 返回分量分布：

可能存在的问题  (1)

CopulaDistribution 不接受 ProductDistribution 作边缘：

在列表中输入所有分布的正确语法：

巧妙范例  (2)

具有均匀边缘分布的一些 copula 核：

具有不同边缘分布的一个 Frank copula：

Wolfram Research (2010)，CopulaDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CopulaDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，CopulaDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CopulaDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "CopulaDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/CopulaDistribution.html.

APA

Wolfram 语言. (2010). CopulaDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CopulaDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_copuladistribution, author="Wolfram Research", title="{CopulaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/CopulaDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_copuladistribution, organization={Wolfram Research}, title={CopulaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/CopulaDistribution.html}, note=[Accessed: 14-November-2024 ]}