DSolveChangeVariables
DSolveChangeVariables[dsolve,u,t,trans]
changes the solution function in dsolve to ![]() using the transformation trans.
using the transformation trans.
DSolveChangeVariables[dsolve,{u1,u2,…},t,trans]
changes the solution functions in the system to ![]() .
.
DSolveChangeVariables[dsolve,u,{t1,…,tn},trans]
changes the solution function in the partial differential equation to ![]() .
.
Details and Options


- A change of variables is often used to simplify the coefficients in a differential expression or to represent it in a more suitable coordinate system such as polar coordinates to exploit the symmetry in the problem.
- DSolveChangeVariables can be used to perform a change of variables for a single ordinary differential equation or partial differential equation without initial or boundary conditions.
- The change of variables is performed using the chain rule
- on an interval
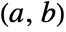 or
or - over a region
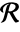 where
where 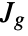 denotes the Jacobian of function
denotes the Jacobian of function 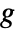 with respect to its arguments.
with respect to its arguments. - The possible forms for dsolve are the forms supported by DSolve:
-
DSolve[deq,y,x] ordinary differential equation DSolve[{deq1,…,deqn},{y1,…,yn},x] system of differential equations DSolve[deq,z,{x,y,…}] partial differential equation - Either an unevaluated DSolve[…] or Inactive[DSolve][…] can be used. It is important that the dsolve does not evaluate, so the safe method is to use Inactive[DSolve][…], which can be produced through Inactivate[dsolve,DSolve].
- DSolveChangeVariables returns the result in the form Inactive[DSolve][…]. Use Activate to solve the differential equation in the new coordinates. »
- The transformation trans can have the forms:
-
t==ϕ[x] replace ϕ[x] by t {u==ϕ[x,y,…],v=ψ[x,y,…],…} replace ϕ[x,y,…] by u and ψ[x,y,…] by v, etc. chart1chart2 named coordinate systems from CoordinateChartData - The transformation
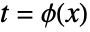 is assumed to be differentiable on its domain of definition.
is assumed to be differentiable on its domain of definition. - When using named coordinate systems, the transformation can be entered in any form accepted by CoordinateTransformData, including {oldsys,metric,dim}{newsys,metric,dim}, {oldsysnewsys,metric,dim} and the various more abbreviated forms.
- Restrictions on the domains of the variables and parameters in the differential expression can be specified using Assumptions.
Examples
open allclose allBasic Examples (4)
Apply the change of variables ![]() to a linear differential equation:
to a linear differential equation:
Solve the differential equation:
Apply the change of variables ![]() to a nonlinear differential equation:
to a nonlinear differential equation:
Transform the 2D Laplace equation from Cartesian to the polar coordinate system:
Apply the change of variables ![]() to a linear ordinary differential equation:
to a linear ordinary differential equation:
Solve the resulting differential equation and substitute back to the original variable:
Compare the result with the solution to the original ordinary differential equation:
Scope (18)
Ordinary Differential Equations (6)
Simplify a second-order linear differential equation with a change of variables:
Transform the nonlinear Riccati equation to a linear ODE with the change of variables ![]() :
:
Apply the trigonometric transformation ![]() to an ordinary differential equation:
to an ordinary differential equation:
Apply the complex-valued transformation ![]() and
and ![]() to an ordinary differential equation:
to an ordinary differential equation:
Apply the change of variables ![]() to a differential equation:
to a differential equation:
Reduce a variable-coefficient nonlinear ODE to a constant-coefficient equation using ![]() :
:
Partial Differential Equations (5)
Transform the ![]() -dimensional wave equation into null coordinates:
-dimensional wave equation into null coordinates:
Apply the same transformation but express the old coordinates in terms of the new ones:
Apply the change of variables ![]() to the heat equation:
to the heat equation:
Apply the change of variables ![]() and
and ![]() to a partial differential equation:
to a partial differential equation:
Apply the change of variables ![]() and
and ![]() to a partial differential equation:
to a partial differential equation:
Make a purely symbolic transformation to a partial differential equation:
Partial Differential Equations and Named Coordinate Systems (7)
Transform a 3D Poisson's equation from Cartesian to the cylindrical coordinate system:
Transform the 3D wave equation from Cartesian to the cylindrical coordinate system:
Transform the 3D biharmonic equation from Cartesian to the spherical coordinate system:
Transform the 3D heat equation in spherical coordinates back to the Cartesian coordinates:
Transform a three-dimensional Schrödinger in spherical coordinates to cylindrical coordinates:
Express the 4D Laplace equation in hyperspherical coordinates:
Transform Poisson's equation on the sphere from standard angular to stereographic coordinates:
Applications (6)
In quantum mechanics, the operator ![]() is a multiple of the angular momentum in the
is a multiple of the angular momentum in the ![]() direction. Show this by transforming the equation
direction. Show this by transforming the equation ![]() to polar coordinates:
to polar coordinates:
Consider the Cauchy–Euler equation ![]() . It is possible to transform this ODE into an equation with constant coefficients by applying the change of variables
. It is possible to transform this ODE into an equation with constant coefficients by applying the change of variables ![]() :
:
Apply the transformation ![]() to the linear second-order ordinary differential equation
to the linear second-order ordinary differential equation ![]() :
:
Dividing the transformed equation by ![]() leads to a drastically simplified differential equation:
leads to a drastically simplified differential equation:
A spherically symmetric solution to the heat equation ![]() in three dimensions can be reduced to a linear ODE. First, write out the equation in spherical coordinates:
in three dimensions can be reduced to a linear ODE. First, write out the equation in spherical coordinates:
Then change to a function of a single variable ![]() that combines both space and time coordinates:
that combines both space and time coordinates:
In the heat-mass transfer problem, an equation takes the form ![]() , where
, where ![]() is a constant,
is a constant, ![]() is the distance from the origin, and
is the distance from the origin, and ![]() is a modification of the polar angle. Starting from standard spherical coordinates, express this equation in local coordinates, then show it can be reduced to Poisson's equation. Set
is a modification of the polar angle. Starting from standard spherical coordinates, express this equation in local coordinates, then show it can be reduced to Poisson's equation. Set ![]() equal to a constant and use DSolveChangeVariables to change how the polar angle is expressed:
equal to a constant and use DSolveChangeVariables to change how the polar angle is expressed:
Create an operator to express the Laplacian in these coordinates:
Change to new independent variable using ![]() :
:
Divide out the exponential and isolate the term free of the derivatives on the right-hand side:
The left-hand side is the Laplacian in modified spherical coordinates, confirming this is Poisson's equation:
Apply the separation of variables transformation to a Heat equation–type partial differential equation:
After dividing by ![]() , you can see that the variables are separated:
, you can see that the variables are separated:
Properties & Relations (2)
A result always has an inactive head, irrespective of the form of input:
DSolveChangeVariables effectively uses the "Mapping" property of CoordinateTransformData:
Possible Issues (1)
DSolveChangeVariables transforms differential operators, here giving ![]() :
:
Linear differential operators can be transformed as vector fields, though TransformedField will express the result in terms of orthonormal bases, here giving ![]() :
:
Text
Wolfram Research (2022), DSolveChangeVariables, Wolfram Language function, https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.
CMS
Wolfram Language. 2022. "DSolveChangeVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.
APA
Wolfram Language. (2022). DSolveChangeVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DSolveChangeVariables.html