DiscretizeRegion[reg]
discretizes a region reg into a MeshRegion.
DiscretizeRegion[reg,{{xmin,xmax},…}]
restricts to the bounds ![]() .
.




DiscretizeRegion
DiscretizeRegion[reg]
discretizes a region reg into a MeshRegion.
DiscretizeRegion[reg,{{xmin,xmax},…}]
restricts to the bounds ![]() .
.
Details and Options

- DiscretizeRegion is also known as mesh generation and grid generation.
- DiscretizeRegion discretizes the interior and boundaries of the region reg.
- In particular, DiscretizeRegion will attempt to discretize lower-dimensional parts of reg.
- The region reg can be anything that is ConstantRegionQ and RegionEmbeddingDimension less than or equal to 3.
- DiscretizeRegion has the same options as MeshRegion, with the following additions and changes:
-
AccuracyGoal Automatic digits of accuracy sought MaxCellMeasure Automatic maximum cell measure MeshQualityGoal Automatic quality goal for mesh cells Method Automatic method to use MeshRefinementFunction None function that returns True if a mesh cell needs refinement PerformanceGoal $PerformanceGoal whether to consider speed or quality PrecisionGoal Automatic digits of precision sought - With MeshRefinementFunction->f, the function f[vlist,m] is applied to each simplex created, where vlist is a list of the vertices and m is the measure. If f[vlist,m] returns True, the simplex will be refined.
- With AccuracyGoal->a and PrecisionGoal->p, an attempt will be made to keep the maximum distance between the region reg or the discretized region dreg and any point in RegionSymmetricDifference[reg,dreg] to less than
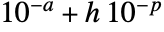 , where
, where 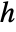 is the length of the diagonal of the bounding box.
is the length of the diagonal of the bounding box.

Examples
open all close allBasic Examples (3)
Scope (30)
Regions in 1D (5)
Point and Line are special regions that can exist in 1D:
Line:
An ImplicitRegion is 1D if it has only one variable:
Because this region is unbounded, clip it to discretize:
A ParametricRegion is 1D if it has only one function:
The discretization can be clipped to a specified range:
Because this region is unbounded, clip it to discretize:
A BooleanRegion in 1D:
Regions in 2D (8)
Point, Circle, and Rectangle are special regions that can exist in 2D:
Circle is 1D, but embedded in 2D:
Rectangle is 2D:
An ImplicitRegion is 2D if it has two variables. A 1D region is typically an equation:
A 2D region is typically a combination of inequalities:
For an unbounded region, clip the discretization to a specified range:
A ParametricRegion is 2D if it has two functions. A 1D region has one parameter:
A 2D region has two parameters:
A 2D parametric region with parameters constrained to a unit disk:
When the parameters are constrained to just the unit circle, the result is 1D:
Parameters may be members of mixed-dimension regions:
Given two exact regions, ParametricRegion can be used to represent their Minkowski sum:
A RegionUnion in 2D:
A region can include components of different dimensions:
Separate the components by dimension:
A polygon with GeoGridPosition:
A polygon with GeoPosition:
Regions in 3D (8)
Point, Line, Polygon, and Ellipsoid are special regions that can exist in 3D:
Line:
An ImplicitRegion is 3D if it has three variables. A 2D region is typically an equation:
Clip an unbounded region to discretize it:
A ParametricRegion with 3 functions and a 3D parameters space is a 3D solid:
A ParametricRegion with 3 functions and a 2D parameter space is a surface embedded in 3D:
Parameters constrained to the lower surface of a sphere are in a 2D parameter space:
A ParametricRegion with 3 functions and a 1D parameter space is a curve embedded in 3D:
The parameters can be part of mixed-dimension region:
Discretize a ParametricRegion where the parameters are in a mixed-dimension region:
The result has 1D, 2D, and 3D components:
Given two exact regions, ParametricRegion can be used to represent their Minkowski sum:
Detail (2)
The measure of cells in the discretization can be controlled using MaxCellMeasure:
By default, when given as a number, it applies to the embedding dimension:
A particular dimension may be specified explicitly:
For nonlinear regions the measure of boundary cells depends on several options:
The length of any segment may be controlled by MaxCellMeasure:
The default PrecisionGoal is chosen to be a value so that curves appear as visually smooth:
PrecisionGoal->None may be used to base the boundary measure on MaxCellMeasure:
AccuracyGoal->a may be used to specify an absolute tolerance ![]() :
:
The default is for MaxCellMeasure to apply to the embedding dimension:
The measure on the boundary may be further restricted by approximation requirements:
Quality (7)
The measure of cells in the discretization can be controlled using MaxCellMeasure:
By default, this applies only to full-dimensional cells:
MaxCellMeasure can also control the size of lower-dimensional cells:
The quality of cells in the discretization can be controlled using MeshQualityGoal:
The goal can also be set to "Minimal" or "Maximal":
MeshRefinementFunction can be used to refine a discretization based on a function:
Add a refinement function to refine triangles in the upper-left quadrant:
Use AccuracyGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher AccuracyGoal is closer to the true boundary:
Use PrecisionGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher PrecisionGoal is closer to the true boundary:
Set PerformanceGoal to "Quality" for a high-quality discretization:
Or to "Speed" for a faster discretization that may be of lower quality:
Options (28)
AccuracyGoal (1)
Use AccuracyGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher AccuracyGoal is closer to the true boundary:
MaxCellMeasure (4)
Discretize a polygon using the Automatic setting for MaxCellMeasure:
Specify a minimal triangulation by not constraining cell measure:
This gives the areas of the triangles:
Specify a maximum length for line segments:
A Histogram of the line segment lengths:
In 3D, specify a maximum area for faces:
A Histogram of the face areas:
MeshCellHighlight (3)
MeshCellHighlight allows you to specify highlighting for parts of a MeshRegion:
By making faces transparent, the internal structure of a 3D MeshRegion can be seen:
MeshCellLabel (3)
MeshCellLabel can be used to label parts of a MeshRegion:
Label the vertices and edges of a polygon:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a MeshRegion:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction allows you to specify functions for parts of a MeshRegion:
MeshCellStyle (3)
MeshCellStyle allows you to specify styling for parts of a MeshRegion:
By making faces transparent, the internal structure of a 3D MeshRegion can be seen:
MeshRefinementFunction (2)
Method (6)
The "Continuation" method uses a curve continuation method that can in many cases resolve corners, cusps, and sharp changes quite well:
The "RegionPlot" method is based on improving output from RegionPlot and can sometimes be faster:
The "Boolean" method is optimized for Boolean regions:
The "DiscretizeGraphics" method is optimized for graphics primitives:
The "RegionPlot3D" method for 3D regions is based on RegionPlot3D:
The "ContourPlot3D" method for 3D regions is based on ContourPlot3D:
PrecisionGoal (1)
Use PrecisionGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher PrecisionGoal is closer to the true boundary:
Applications (2)
Properties & Relations (5)
The output of DiscretizeRegion is a MeshRegion:
TriangulateMesh can be used to re-discretize a MeshRegion:
Only discretizing the original region can more accurately discretize the boundary, though:
Applied to a MeshRegion, DiscretizeRegion is the same as TriangulateMesh:
DiscretizeRegion can discretize a region with holes:
DiscretizeRegion can discretize a region with disjoint components:
See Also
MeshRegion BoundaryDiscretizeRegion TriangulateMesh DiscretizeGraphics FindMeshDefects RepairMesh RegionImage
Function Repository: IntrinsicCurvedManifoldToGraph
Related Guides
Text
Wolfram Research (2014), DiscretizeRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscretizeRegion.html (updated 2015).
CMS
Wolfram Language. 2014. "DiscretizeRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DiscretizeRegion.html.
APA
Wolfram Language. (2014). DiscretizeRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscretizeRegion.html
BibTeX
@misc{reference.wolfram_2025_discretizeregion, author="Wolfram Research", title="{DiscretizeRegion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DiscretizeRegion.html}", note=[Accessed: 08-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_discretizeregion, organization={Wolfram Research}, title={DiscretizeRegion}, year={2015}, url={https://reference.wolfram.com/language/ref/DiscretizeRegion.html}, note=[Accessed: 08-December-2025]}