ExponentialGeneratingFunction
ExponentialGeneratingFunction[expr,n,x]
给出 x 序列的指数母函数,其中第 n![]() 项由表达式 expr 给出.
项由表达式 expr 给出.
ExponentialGeneratingFunction[expr,{n1,n2,…},{x1,x2,…}]
给出 x1,x2,… 序列的多维指数母函数,其中第 n1,n2,… 项由 expr 给出.
更多信息和选项

- 第
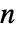 项是
项是 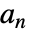 的序列的指数母函数由
的序列的指数母函数由 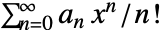 .
. - 多维指数母函数由
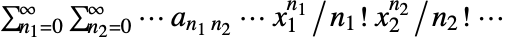 给出.
给出. - 可以给出下列选项:
-
Assumptions $Assumptions 关于参数的假设 GenerateConditions False 是否生成关于参数条件的结果 Method Automatic 使用的方法 VerifyConvergence True 是否验证收敛
范例
打开所有单元关闭所有单元范围 (19)
基本用法 (6)
用 Plot3D、ContourPlot 或 DensityPlot 来绘制幅值:
用 ParametricPlot3D 在复平面绘制频谱:
ExponentialGeneratingFunction 将使用包括线性的几个属性:
ExponentialGeneratingFunction 自动作用于列表的各项:
特殊序列 (13)
对于超几何项序列,DiscreteRatio 是有理式:
DifferenceRoot 推广可得 DifferentialRoot 函数:
选项 (5)
GenerateConditions (1)
用 GenerateConditions 生成有效条件:
VerifyConvergence (3)
设置 VerifyConvergence 为 False,将母函数视为形式对象:
设置 VerifyConvergence 为 True,将验证收敛半径非零:
另外设置 GenerateConditions 为 True,将显示收敛条件:
属性和关系 (3)
ExponentialGeneratingFunction 有效计算一个无穷和:
可能存在的问题 (1)
文本
Wolfram Research (2008),ExponentialGeneratingFunction,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
CMS
Wolfram 语言. 2008. "ExponentialGeneratingFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
APA
Wolfram 语言. (2008). ExponentialGeneratingFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html 年