GeneralizedLinearModelFit

GeneralizedLinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

各変数 x の値について yiをフィットする の形式の一般化された線形モデルを構築する．

GeneralizedLinearModelFit[data,{f1,f2,…},{x1,x2,…}]

fi が変数 xk に依存する という形式の一般化された線形モデルを構築する．

GeneralizedLinearModelFit[{m,v}]

計画行列 m と応答ベクトル v から一般化された線形モデルを構築する．

詳細とオプション

  • GeneralizedLinearModelFitは，一般的な可逆関数（リンク関数）によって変換された関数の線形結合を使って入力データをモデル化しようとする．
  • GeneralizedLinearModelFitは，もとの 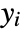は，平均 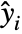の指数関数族分布に従う独立観察で，関数 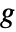は可逆リンク関数であるという仮定のもとに　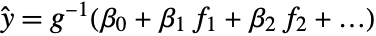の形の一般化された線形モデルを作成する．
  • ExponentialFamilyオプションは分布を制御し，LinkFunctionオプションは 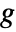の形式を制御する．
  • GeneralizedLinearModelFitは，自身が構築した一般化された線形モデルを表す記号的なFittedModelオブジェクトを返す．モデルの特性と診断は model["property"]で得ることができる．
  • 特定の点 x1, … におけるGeneralizedLinearModelFitからの最もよくフィットした関数の値は model[x1,…]で得ることができる．
  • 次は，data の可能な形である．
  • {y1,y2,…}{{1,y1},{2,y2},…}という形式に等しい
    {{x11,x12,…,y1},…}独立した値 xijと応答 yiのリスト
    {{x11,x12,…}y1,…}入力値と応答の間の規則のリスト
    {{x11,x12,…},…}{y1,y2,…}入力値のリストと応答の間の規則
    {{x11,…,y1,…},…}n行列の第 n 列をフィットする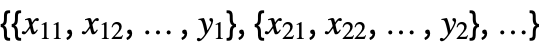
  • {{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}のような多変量のデータの場合，座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない．
  • さらに，data は，関数および変数を指定しなくても計画行列を使って指定できる．
  • {m,v}計画行列 m と対応ベクトル v
  • GeneralizedLinearModelFit[m,v]の計画行列 m は，{{f1,f2,…},{f1,f2,…},…}の形のデータ点における基底関数 fiの値によって形成される．応答ベクトル v は応答のリスト{y1,y2,…}である．
  • 計画行列 m と応答ベクトル v についてのモデルは 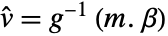である．ここで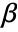， は推定すべきパラメータのベクトルである．
  • 計画行列が使われるとき，基底関数 fiはGeneralizedLinearModelFit[{m,v},{f1,f2,…}]の形を使って指定できる．
  • GeneralizedLinearModelFitは次のオプションを取る．
  • AccuracyGoalAutomatic目標確度
    ConfidenceLevel 95/100母数と予測の信頼水準
    CovarianceEstimatorFunction "ExpectedInformation"母数共分散行列のための推定法
    DispersionEstimatorFunction Automatic分散母数を推定する関数
    ExponentialFamily Automaticy の指数型分布族
    IncludeConstantBasis True定数基底関数を入れるかどうか
    LinearOffsetFunction None線形予測器における既知のオフセット
    LinkFunction Automaticモデルのリンク関数
    MaxIterationsAutomatic使用する最大反復回数
    NominalVariables None名義的とみなされる変数
    PrecisionGoalAutomatic目標とする精度
    Weights Automaticデータ要素の重み
    WorkingPrecision Automatic内部計算で使われる精度
  • IncludeConstantBasis->Falseの設定では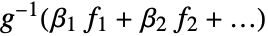，の形式のモデルがフィットされる．
  • LinearOffsetFunction->h の設定では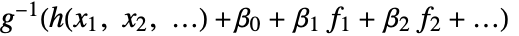，の形式のモデルがフィットされる．
  • ConfidenceLevel->p のとき，確率 p の信頼区間は母数と予測区間について計算される．
  • DispersionEstimatorFunction->f と設定すると，共通分散は f[y,,w]で推定される．ただし，y={y1,y2,…}は観察値のリスト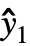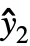，={,,…}は予測値のリスト，w={w1,w2,…}は測度 yiの重みのリストである．
  • ExponentialFamilyの可能な設定値は，"Gaussian"，"Binomial"，"Poisson"，"Gamma"，"InverseGaussian"，"QuasiLikelihood"である．
    • 特性
  • model["property"]を使って得られるデータとフィットされた関数に関する特性
  • "BasisFunctions"基底関数のリスト
    "BestFit"フィットされた関数
    "BestFitParameters"母数の推定
    "Data"入力データあるいは計画行列と反応ベクトル
    "DesignMatrix"モデルのための計画行列
    "Function"最もよくフィットした純関数
    "LinearPredictor"フィットされた線形結合
    "Response"入力データの応答値
    "Weights"データのフィットに使用する重み
  • 分散とモデルからの逸脱に関連する特性
  • "Deviances"逸脱度
    "DevianceData"逸脱度表のデータ集合
    "EstimatedDispersion"予測分散母数
    "NullDeviance"ヌルモデルの逸離度
    "NullDegreesOfFreedom"ヌルモデルの自由度
    "ResidualDeviance"フィットされたモデルの逸度とフルモデルの逸離度の差
    "ResidualDegreesOfFreedom"モデル自由度とヌル自由度の差
  • 残差のタイプ
  • "AnscombeResiduals"アンスコム(Anscombe)残差
    "DevianceResiduals"逸脱度残差
    "FitResiduals"実際の応答と予想された応答の差
    "LikelihoodResiduals"尤度残差
    "PearsonResiduals"ピアソン(Pearson)残差
    "StandardizedDevianceResiduals"標準化された逸脱度残差
    "StandardizedPearsonResiduals"標準化されたピアソン残差
    "WorkingResiduals"作業残差
  • 母数推定の特性と診断
  • "CorrelationMatrix"漸近的な母数相関行列
    "CovarianceMatrix"漸近的な母数共分散行列
    "ParameterEstimates"フィットされたパラメータ情報の表
  • 影響力の統計量関連特性
  • "CookDistances"クック(Cook)の距離のリスト
    "HatDiagonal"ハット行列の対角要素
  • 予測値特性
  • "PredictedResponse"データのフィットされた値
  • 適合度尺度の特性
  • "AdjustedLikelihoodRatioIndex"Ben‐AkivaとLermanの修正尤度比指数
    "AIC"赤池情報量基準
    "BIC"ベイズ(Bayes)情報量基準
    "CoxSnellPseudoRSquared"CoxとSnellの擬似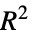
    "CraggUhlerPseudoRSquared"CraggとUhlerの擬似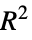
    "EfronPseudoRSquared"Efronの擬似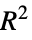
    "LikelihoodRatioIndex"McFaddenの尤度比指数
    "LikelihoodRatioStatistic"尤度比
    "LogLikelihood"フィットされたモデルのための対数尤度
    "PearsonChiSquare"ピアソンの 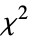統計

例題

すべて開くすべて閉じる

例  (1)

データ集合を定義する：

対数線形ポアソン(Poisson)モデルをデータにフィットする：

モデルの関数形を見る：

ある点でモデルを評価する：

データ点とモデルをプロットする：

モデルの逸脱度残差を計算し，プロットする：

スコープ  (15)

データ  (8)

整数に依存しない値が増加すると仮定して，成功確率応答でデータをフィットする：

これは以下に等しい：

変数が2つ以上のモデルをフィットする：

データを予測変数関数の線形結合にフィットする：

規則のリストをフィットする：

入力値と応答の規則をフィットする：

応答として列を指定する：

カテゴリ予測変数を持つモデルをフィットする：

モデルの逸脱度表を得る：

計画行列と応答ベクトルで与えられるモデルをフィットする：

関数形を見る：

基底関数をxとyとして参照するモデルをフィットする：

一般化された線形モデルで使用可能な特性のリストを得る：

特性  (7)

データとフィットされた関数  (1)

一般化された線形モデルをフィットする：

もとのデータを抽出する：

最高のフィットを求め，プロットする：

フィットされた関数を純関数として求める：

フィットの計画行列と応答ベクトルを得る：

残差  (1)

フィットの残差を調べる：

生の残差を可視化する：

アンスコム残差と標準化されたピアソン残差をステムプロットで可視化する：

分散と逸脱度  (1)

ガンマ回帰モデルをデータにフィットする：

推定分散を求める：

各点の逸脱度をプロットする：

逸脱度分析表のデータ集合を得る：

表から逸脱度残差を得る：

母数推定診断  (1)

母数情報のフォーマットされた表を得る：

z 統計値の列を抽出する：

影響力の統計量  (1)

極値を含むデータをロジットモデルにフィットする：

クック距離をチェックして大きく影響する点を確認する：

ハット行列の対角要素をチェックして点がフィットに与える影響を評価する：

予測値  (1)

逆ガウスモデルをフィットする：

予測値を観測値に対してプロットする：

適合度尺度  (1)

対数線形ポアソンモデルの適合度尺度表を得る：

予測変数のすべての部分集合について適合度尺度を計算する：

AICによってモデルにランクを付ける：

一般化と拡張  (1)

モデルの関数形に対して他の数学操作を行う：

記号積分と数値積分を行う：

モデルの特定の値を与える予測値を求める：

オプション  (10)

ConfidenceLevel  (1)

デフォルト設定では95%の信頼区間が使われる：

代りに99%の区間を使う：

FittedModel内でレベルを90%に設定する：

CovarianceEstimatorFunction  (1)

一般化された線形モデルをフィットする：

期待される情報行列を使って共分散行列を計算する：

観察された情報行列を代りに使う：

DispersionEstimatorFunction  (1)

二項モデルをフィットする：

共分散行列を計算する：

ピアソンの による分散を推定して共分散行列を計算する：

ExponentialFamily  (1)

データを単純な線形回帰モデルにフィットする：

正準ガンマ回帰モデルにフィットする：

正準逆ガウス回帰モデルにフィットする：

IncludeConstantBasis  (1)

単純な線形回帰モデルをフィットする：

ゼロ切片を持つ線形モデルをフィットする：

LinearOffsetFunction  (1)

データを正準ガンマ回帰モデルにフィットする：

データを既知のSqrt[x]項を持つガンマ回帰モデルにフィットする：

LinkFunction  (1)

正準Logリンクを持つポアソンモデルをフィットする：

名前付きのリンクを使う：

シフトされたSqrtリンクに純関数を使う：

NominalVariables  (1)

第1変数を名義変数として扱ってデータをフィットする：

両方の変数を名義変数として扱う：

Weights  (1)

等しい重みを使ってモデルをフィットする：

データ点のための明示的な重みを与える：

WorkingPrecision  (1)

WorkingPrecisionを使ってより高精度の母数推定を得る：

フィットされた関数を得る：

フィットの後，特性計算で精度を落とす：

アプリケーション  (2)

いくつかの確率データをシミュレーションする：

一般化された二項線形モデルをフィットして，さまざまなリンク関数と覚的に比較する：

分割表からの計数データをポアソンの対数線形モデルにフィットする：

数，予想される値，標準化された残差を表形式で表示する：

特性と関係  (5)

DesignMatrixはGeneralizedLinearModelFitで使われる計画行列を構築する：

デフォルトで，GeneralizedLinearModelFitとLinearModelFitは等しいモデルをフィットする：

デフォルトの"Binomial"モデルはLogitModelFitのためのモデルに等しい：

ProbitModelFitは"ProbitLink"を伴う"Binomial" モデルに等しい：

GeneralizedLinearModelFitは，TimeSeriesのタイムスタンプを変数として用いる：

タイムスタンプを再スケールし，フィットし直す：

値についてのフィットを求める：

GeneralizedLinearModelFitは，複数の経路があるTemporalDataについては，経路ごとに作用する：

Wolfram Research (2008), GeneralizedLinearModelFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

テキスト

Wolfram Research (2008), GeneralizedLinearModelFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

CMS

Wolfram Language. 2008. "GeneralizedLinearModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

APA

Wolfram Language. (2008). GeneralizedLinearModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html

BibTeX

@misc{reference.wolfram_2024_generalizedlinearmodelfit, author="Wolfram Research", title="{GeneralizedLinearModelFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_generalizedlinearmodelfit, organization={Wolfram Research}, title={GeneralizedLinearModelFit}, year={2008}, url={https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}, note=[Accessed: 21-November-2024 ]}