GeneralizedLinearModelFit

GeneralizedLinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

构建一个形式为 的广义线性模型，该模型对于每个 xi 都拟合 yi.

GeneralizedLinearModelFit[data,{f1,f2,…},{x1,x2,…}]

构建形式为 的广义线性模型，其中 fi 依赖于变量 xk.

GeneralizedLinearModelFit[{m,v}]

按照设计矩阵 m 和响应向量 v 构建一个广义线性模型.

更多信息和选项

  • GeneralizedLinearModelFit 尝试用一个由通用可逆函数（链接函数）转换的函数的线性组合对输入数据进行建模.
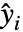  • 假设原 是独立的观察值，服从均值为 的指数分布族，并且函数 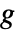是一个可逆链接函数，则 GeneralizedLinearModelFit 产生形式为 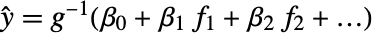的广义线性模型.
  • ExponentialFamily 选项控制分布，而 LinkFunction 选项控制 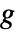的形式.
  • GeneralizedLinearModelFit 返回一个符号 FittedModel 对象，表示其构建的广义线性模型. 模型的属性以及诊断信息可以从 model["property"] 得到.
  • GeneralizedLinearModelFit 在特定点 x1、… 的最佳拟合函数的值可以从 model[x1,…] 得到.
  • data 的可能形式包括：
  • {y1,y2,…}等价于形式 {{1,y1},{2,y2},…}
    {{x11,x12,…,y1},…}一个独立值列表 xij 及响应 yi
    {{x11,x12,…}y1,…}输入值和响应之间的规则列表
    {{x11,x12,…},…}{y1,y2,…}输入值和响应列表之间的规则
    {{x11,…,y1,…},…}n拟合矩阵的第 n 列
  • 对于多变量数据，如 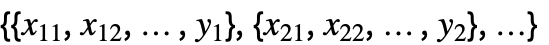{{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}， 坐标 xi1, xi2, … 的数量应该等于变量 xi 的数量.
  • 此外，可以使用设计矩阵来指定 data，而无需指定函数和变量：
  • {m,v}设计矩阵 m 和响应向量 v
  • 在 GeneralizedLinearModelFit[m,v] 中，设计矩阵 m 是由数据点上的基函数 fi 的值形成的，形式为 {{f1,f2,…},{f1,f2,…},…}. 响应向量 v 是响应 {y1,y2,…} 的列表.
  • 对于设计矩阵 m 和响应向量 v，模型是 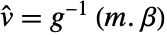，其中 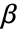是要计算的参数向量.
  • 当使用设计矩阵时，基函数 fi 可以用 GeneralizedLinearModelFit[{m,v},{f1,f2,…}] 形式指定.
  • GeneralizedLinearModelFit 采用下列选项：
  • AccuracyGoalAutomatic搜索的准确度
    ConfidenceLevel 95/100参数和预测的置信度
    CovarianceEstimatorFunction "ExpectedInformation"参数协方差矩阵的估计方法
    DispersionEstimatorFunction Automatic估计变异参数的函数
    ExponentialFamily Automaticy 的指数分布族
    IncludeConstantBasis True是否包含一个常数基函数
    LinearOffsetFunction None线性预测器的已知偏移
    LinkFunction Automatic模型的链接函数
    MaxIterationsAutomatic使用迭代的最大数量
    NominalVariables None名义变量
    PrecisionGoalAutomatic搜索的精度
    Weights Automatic数据元素的权重
    WorkingPrecision Automatic内部计算的精度
  • 在 IncludeConstantBasis->False 设置下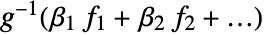， 形式的模型是拟合的.
  • 在 LinearOffsetFunction->h 设置下，形如 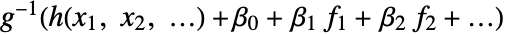的模型是拟合的.
  • 在 ConfidenceLevel->p 下，对参数和预测区间计算概率 p 的置信区间.
  • 在设置 DispersionEstimatorFunction->f 下，普通变异按 f[y,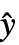,w] 估计，其中 y={y1,y2,…} 是观测值列表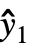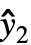，={,,…} 是预测值列表， w={w1,w2,…} 是测量 yi 的权重列表.
  • ExponentialFamily 的可能设置包括："Gaussian"、"Binomial"、"Poisson"、"Gamma"、 "InverseGaussian" 或 "QuasiLikelihood".
    • 属性
  • 用 model["property"] 得到的与数据和拟合函数相关的属性包括：
  • "BasisFunctions"基函数列表
    "BestFit"拟合函数
    "BestFitParameters"参数估计
    "Data"输入数据或设计矩阵和响应向量
    "DesignMatrix"模型的设计矩阵
    "Function"最佳拟合的纯函数
    "LinearPredictor"拟合线性组合
    "Response"输入数据中的响应值
    "Weights"用于拟合数据的权重
  • 与散布和模型变异相关的属性包括：
  • "Deviances"变异
    "DevianceData"变异表格数据集
    "EstimatedDispersion"估计扩散参数
    "NullDeviance"空模型的变异
    "NullDegreesOfFreedom"空模型的自由度
    "ResidualDeviance"拟合模型的偏差与完全模型偏差之间的差异
    "ResidualDegreesOfFreedom"模型自由度和空自由度之间的差异
  • 残差类型包括：
  • "AnscombeResiduals"Anscombe 残差
    "DevianceResiduals"变异残差
    "FitResiduals"实际响应和预测响应的不同
    "LikelihoodResiduals"似然残差
    "PearsonResiduals"Pearson 残差
    "StandardizedDevianceResiduals"标准化变异残差
    "StandardizedPearsonResiduals"标准化 Pearson 残差
    "WorkingResiduals"工作残差
  • 参数估计的属性和诊断信息包括：
  • "CorrelationMatrix"渐近的参数相关矩阵
    "CovarianceMatrix"渐近的参数协方差矩阵
    "ParameterEstimates"拟合参数信息表
  • 影响度量的属性包括
  • "CookDistances"库克距离列表
    "HatDiagonal"帽子矩阵的对角元素
  • 预测值的属性包括：
  • "PredictedResponse"数据的拟合值
  • 衡量拟合优度的属性包括：
  • "AdjustedLikelihoodRatioIndex"Ben‐Akiva 和 Lerman 似然比指数
    "AIC"赤池信息量准则
    "BIC"贝叶斯信息量准则
    "CoxSnellPseudoRSquared"Cox 和 Snell 拟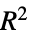
    "CraggUhlerPseudoRSquared"Cragg 和 Uhler 拟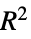
    "EfronPseudoRSquared"Efron 拟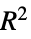
    "LikelihoodRatioIndex"McFadden 似然比指数
    "LikelihoodRatioStatistic"似然比
    "LogLikelihood"拟合模型的对数似然
    "PearsonChiSquare"Pearson 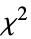统计

范例

打开所有单元关闭所有单元

基本范例  (1)

定义一个数据集：

拟合对数-线性的泊松模型：

查看模型的函数形式：

计算模型在某个点的值：

绘制数据点和模型：

计算并绘制模型的异常误差：

范围  (15)

数据  (8)

用成功概率响应拟合数据，假设与整数无关的数值不断增加：

这等价于：

拟合具有不止一个变量的模型：

拟合预测变量函数的线性组合：

拟合规则列表：

拟合输入值和响应的规则：

指定一个列作为响应：

拟合分类预测变量的模型：

得到模型的一个异常表：

拟合一个设计矩阵和响应变量给出的模型：

查看函数形式：

拟合以 x 和 y 为参数的基函数的模型：

得到一个广义线性模型的可用属性列表：

属性  (7)

数据及拟合函数  (1)

拟合一个广义线性模型：

提取原数据：

得到并绘制最佳拟合：

得到拟合函数，作为一个纯函数：

得到拟合的设计矩阵和响应向量：

残差  (1)

检查拟合的残差：

可视化原始残差：

在图形中，可视化显示 Anscombe 残差和标准化的 Pearson 残差：

散布和异常  (1)

对某些数据拟合伽玛回归模型：

得到估计的散布：

绘制每个点的异常：

得到异常表的分析：

从表格得到残差异常：

参数估计诊断  (1)

得到参数信息的一个格式化表格：

提取 z 统计值的列：

影响度量  (1)

在对数模型中拟合包含极值的某些数据：

检测 Cook 距离，识别更高的影响点：

检测帽子矩阵的对角元素，估算拟合点的影响：

预测值  (1)

拟合一个逆高斯模型：

绘制与观测值相应的预期值：

拟合优度度量  (1)

得到一个对数-线性泊松模型的拟合优度度量的表格：

计算所有预期变量的子集的拟合优度度量：

依据 AIC 排列模型：

推广和延伸  (1)

在模型的函数形式上执行其它的数学运算：

符号积分和数值积分：

求出一个预期值，给出模型的一个特定值：

选项  (10)

ConfidenceLevel  (1)

默认情况下给出 95% 的置信区间：

用 99% 的置信区间：

在 FittedModel 中设置级别为 90%：

CovarianceEstimatorFunction  (1)

拟合广义线性模型：

用预期的信息矩阵计算协方差矩阵：

代替以观察信息矩阵：

DispersionEstimatorFunction  (1)

拟合一个二项模型：

计算协方差矩阵：

计算协方差矩阵，估计 Pearson 的离差：

ExponentialFamily  (1)

拟合一个简单的线性回归模型：

拟合一个标准回归模型：

拟合一个标准逆高斯回归模型：

IncludeConstantBasis  (1)

拟合一个简单的线性回归模型：

拟合截面零的线性模型：

LinearOffsetFunction  (1)

拟合一个标准伽玛回归模型：

拟合有已知 Sqrt[x] 项的一个伽玛回归模型：

LinkFunction  (1)

拟合标准 Log 链接的泊松模型：

使用一个命名链接：

用一个位移 Sqrt 链接的纯函数：

NominalVariables  (1)

拟合数据，将第一个变量视为一个名义变量：

将两个变量视为名义变量：

Weights  (1)

用相等权重拟合模型：

给出数据点的显式的权重：

WorkingPrecision  (1)

用 WorkingPrecision 在参数估计中得到更高的精度：

得到拟合函数：

在拟合后，化简属性计算中的精度：

应用  (2)

模拟某些概率数据：

拟合和可视化比较有各种链接函数的二项广义线性模型：

拟合统计数据，从一个相依表到一个对数-线性模型：

以表格形式显示统计数量，预测值和标准化残差：

属性和关系  (5)

DesignMatrix 用 GeneralizedLinearModelFit 构建设计矩阵：

默认情况下 GeneralizedLinearModelFit 和 LinearModelFit 拟合相等模型：

默认的 "Binomial" 模型等价于 LogitModelFit 模型：

ProbitModelFit 等价于有 "ProbitLink" 的 "Binomial" 模型：

GeneralizedLinearModelFit 会使用 TimeSeries 的时间戳作为变量：

重新缩放时间戳，并且再次拟合：

求值的拟合：

GeneralizedLinearModelFit 按路径逐条应用于多重路径 TemporalData：

Wolfram Research (2008)，GeneralizedLinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

文本

Wolfram Research (2008)，GeneralizedLinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

CMS

Wolfram 语言. 2008. "GeneralizedLinearModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.

APA

Wolfram 语言. (2008). GeneralizedLinearModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html 年

BibTeX

@misc{reference.wolfram_2024_generalizedlinearmodelfit, author="Wolfram Research", title="{GeneralizedLinearModelFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_generalizedlinearmodelfit, organization={Wolfram Research}, title={GeneralizedLinearModelFit}, year={2008}, url={https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}, note=[Accessed: 21-November-2024 ]}