InverseFourierSequenceTransform
InverseFourierSequenceTransform[expr,ω,n]
expr の離散時間フーリエ(Fourier)変換の逆変換を与える.
InverseFourierSequenceTransform[expr,{ω1,ω2,…},{n1,n2,…}]
多次元フーリエ連続変換の逆変換を与える.
詳細とオプション

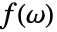 のフーリエ連続変換の逆変換はデフォルトで
のフーリエ連続変換の逆変換はデフォルトで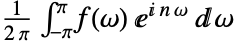 と定義される.
と定義される.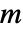 次元逆変換は
次元逆変換は 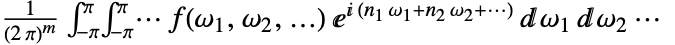 で与えられる.
で与えられる.- InverseFourierSequenceTransform[expr,t,n]の形式において,n は記号でも整数でもよい.
- 使用可能なオプション
-
Assumptions $Assumptions パラメータに関する仮定 FourierParameters {1,1} 変換を定義するパラメータ GenerateConditions False パラメータについての条件を有する結果を生成するかどうか - FourierParametersの一般的な設定には次のようなものがある.
-
{1, 1} 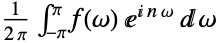
デフォルト設定 {1,-2Pi} 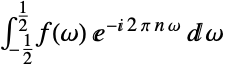
周期1 {a,b} 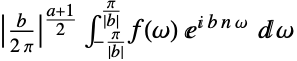
一般設定
例題
すべて開くすべて閉じるオプション (2)
FourierParameters (1)
FourierParametersのデフォルト以外の設定を使う:
特性と関係 (6)
InverseFourierSequenceTransformは積分によって定義される:
InverseFourierSequenceTransformとFourierSequenceTransformは逆関数である:
InverseFourierSequenceTransformはInverseZTransformと密接な関係がある:
InverseFourierTransformがInverseLaplaceTransformと密接な関係があるように:
InverseFourierSequenceTransformはFourierCoefficientと同じである:
InverseFourierSequenceTransformはInverseBilateralZTransformと密接な関係がある:
テキスト
Wolfram Research (2008), InverseFourierSequenceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseFourierSequenceTransform.html.
CMS
Wolfram Language. 2008. "InverseFourierSequenceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseFourierSequenceTransform.html.
APA
Wolfram Language. (2008). InverseFourierSequenceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseFourierSequenceTransform.html