Kurtosis

Kurtosis[data]

data の要素の尖度係数を与える．

Kurtosis[dist]

分布 dist の尖度係数を与える．

詳細

  • Kurtosisは，頂点付近と裾におけるデータの密集度対フランクにおける密集度を測定する．
  • Kurtosis[…]はCentralMoment[…,4]/CentralMoment[…,2]2に等しい．
  • 正規分布の尖度 は3である．正規分布と比較すると以下のようになる．
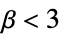
  • 正規分布よりも平たい，緩尖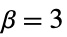
    正規分布，中間的
    正規分布より尖っている，急尖
  • Kurtosis[{{x1,y1,…},{x2,y2,…},…}]は{Kurtosis[{x1,x2,…}],Kurtosis[{y1,y2,…}],…}を返す．
  • Kurtosisは，数値と記号両方の data を扱うことができる．
  • data は，以下の追加的な形式と解釈を持つことがある．
  • Association値（キーは無視される） »
    SparseArrayNormal[data]と等価の配列として »
    QuantityArray配列としての数量 »
    WeightedDataもとになっているEmpiricalDistributionに基づいた重み付き平均 »
    EventDataもとになっているSurvivalDistributionに基づく 　 »
    TimeSeries, TemporalData, …値のベクトルまたは配列（タイムスタンプは無視される） »
    Image,Image3DRGBチャンネルの値またはグレースケールの強度値 »
    Audioすべてのチャンネルの振幅値 »
    DateObject, TimeObject日付のリストまたは時間のリスト
  • ランダム過程 proc について，尖度関数は時点 t におけるスライス分布SliceDistribution[proc,t]について　β[t]=Kurtosis[SliceDistribution[proc,t]]として計算できる． »

例題

すべて開くすべて閉じる

例  (4)

値のリストの尖度：

記号データの尖度：

日付のリストの尖度：

パラメトリック分布の尖度：

スコープ  (23)

基本的な用法  (7)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

WeightedDataの尖度を求める：

EventDataの尖度を求める：

TemporalDataの尖度を求める：

TimeSeriesの尖度を求める：

尖度は値にのみ依存する：

数量を含むデータの尖度を求める：

配列データ  (5)

行列についてのKurtosisは列ごとの尖度を与える：

大きい配列に使うことができる：

Kurtosisは入力がAssociationのときはその値に作用する：

SparseArrayデータは密な配列と同じように使うことができる：

QuantityArrayの尖度を求める：

画像データと音声データ  (2)

RGB画像のチャンネルごとの尖度値：

グレースケール画像の平均強度値：

Kurtosisは，音声オブジェクトについてはチャンネルごとに作用する：

日付と時間  (5)

日付の尖度を計算する：

日付の重み付き尖度を計算する：

異なる暦で与えられた日付の尖度を計算する：

時間の尖度を計算する：

異なる時刻帯指定の時刻の尖度を計算する：

分布と過程  (4)

一変量分布の尖度を求める：

多変量分布の場合：

派生分布についてのKurtosis：

データ分布について：

単位付き数量のある分布の尖度：

ランダム過程についての尖度関数：

アプリケーション  (6)

正規分布のKurtosisの値は3である：

集中分布の尖度は3より大きい：

緩尖分布の尖度は3より小さい：

が無限大に近付くにつれて，BinomialDistributionについての極限分布は正規分布に近付く：

尖度の極限値は3である：

中心極限定理によると，確率変数の正規化された総和の尖度は3に収束する：

平均が0で単位分散を持ち，尖度と歪度でパラメータ化されたピアソン分布を定義する：

1，4，6型のピアソン分布についてのパラメータ不等式を求める：

尖度と歪度の値に依存するピアソン型の領域プロット：

ParetoDistributionからランダムなサンプルを生成する：

モーメントがサンプルモーメントに一致するPearsonDistributionの型を見付ける：

この時系列は，ある人の1ヶ月間の毎日の歩数が含まれている：

歩数の平均：

毎日の歩数が一定している指針として尖度を分析する：

毎日の歩数の頻度のヒストグラムは，分布がMesokurtic（尖度が0）であることを示している：

学級の生徒の身長の尖度を求める：

3より大きい尖度は，分布が平均付近に集中していることを示す：

特性と関係  (5)

データのKurtosisはCentralMomentから計算できる：

分布のKurtosisはCentralMomentから計算できる：

Kurtosisは，TemplateBox[{4}, CentralMoment]⩵Expectation[(x-mu)^4]>=Expectation[(x-mu)^2]^2⩵TemplateBox[{2}, CentralMoment]^2であり，1から下で有界である：

正規分布は値3のKurtosisを持つ：

ほぼ正規の分布は3に近い値のKurtosisを持つ：

この分布の確率密度関数をプロットする：

正規近似の確率密度関数をプロットする：

考えられる問題  (2)

尖度係数は時に過剰尖度係数と混同されることがある：

過剰尖度はNormalDistributionについては消失する：

過剰尖度はCumulant[dist,4]/Cumulant[dist,2]^2と定義される：

尖度はデータについては定義されないことがある：

尖度は分布については定義されないことがある：

おもしろい例題  (1)

20個，100個，300個のサンプルについてのKurtosis推定値の分布：

Wolfram Research (2007), Kurtosis, Wolfram言語関数， https://reference.wolfram.com/language/ref/Kurtosis.html （2024年に更新）.

テキスト

Wolfram Research (2007), Kurtosis, Wolfram言語関数， https://reference.wolfram.com/language/ref/Kurtosis.html （2024年に更新）.

CMS

Wolfram Language. 2007. "Kurtosis." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Kurtosis.html.

APA

Wolfram Language. (2007). Kurtosis. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Kurtosis.html

BibTeX

@misc{reference.wolfram_2024_kurtosis, author="Wolfram Research", title="{Kurtosis}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Kurtosis.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kurtosis, organization={Wolfram Research}, title={Kurtosis}, year={2024}, url={https://reference.wolfram.com/language/ref/Kurtosis.html}, note=[Accessed: 21-December-2024 ]}