Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

LommelS1

See Also
- LommelS2
- HypergeometricPFQ
- HypergeometricPFQRegularized
- BesselJ
- BesselY
- StruveH
- AngerJ
- WeberE
- LommelT1
- LommelT2
Related Guides
- Bessel-Related Functions
- See Also
  - LommelS2
  - HypergeometricPFQ
  - HypergeometricPFQRegularized
  - BesselJ
  - BesselY
  - StruveH
  - AngerJ
  - WeberE
  - LommelT1
  - LommelT2
- Related Guides
  - Bessel-Related Functions

LommelS1

LommelS1[m,n,z]

gives the Lommel function of the first kind .

Details

LommelS1 is also known as a Lommel function of the first kind.
Lommel functions are typically used to represent particular solutions of Bessel-type differential equations.
Mathematical function, suitable for both symbolic and numerical manipulation.
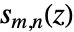satisfies the differential equation . »
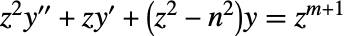LommelS1[m,n,z] has a branch cut discontinuity in the complex z plane running from 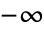to .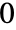
For certain special arguments, LommelS1 automatically evaluates to exact values.
LommelS1 can be evaluated to arbitrary numerical precision.
LommelS1 automatically threads over lists.

Examples

open all close all

Basic Examples (6)

Evaluate numerically:

Evaluate symbolically:

Plot :

Plot over a subset of the complexes:

Expand LommelS1 in a Taylor series at the origin:

Series expansion at a generic point:

Scope (29)

Numerical Evaluation (4)

Evaluate numerically to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex arguments and parameters:

LommelS1 threads elementwise over lists in the last argument:

Compute the matrix LommelS1 function using MatrixFunction:

Specific Values (3)

LommelS1 automatically evaluates to simpler functions for certain parameters:

The exact value of LommelS1 at unity for a specific set of parameters:

LommelS1 is singular whenever or is a non-positive odd integer:

Visualization (3)

Plot the LommelS1 function for and varying :

Plot the LommelS1 function for and varying :

Plot the real part of :

Plot the imaginary part of :

Function Properties (3)

Real domain of LommelS1:

Complex domain of LommelS1:

Singularity and discontinuity information of LommelS1:

has a branch cut discontinuity for :

is a singular point for :

Differentiation (2)

First derivative:

Higher derivatives:

Plot the higher derivatives for , :

Integration (4)

Indefinite integral of LommelS1:

Definite integral of LommelS1:

Integral involving a power function:

More integrals with LommelS1:

Series Expansions (2)

Taylor expansion for LommelS1:

Approximations for around :

Expand LommelS1 in a series around :

Integral Transforms (5)

Compute the Laplace transform using LaplaceTransform:

Compute the Fourier transform of LommelS1:

FourierCosTransform:

FourierSinTransform:

HankelTransform:

MellinTransform:

Function Representations (3)

Relation to the HypergeometricPFQ function:

LommelS1 can be represented in terms of MeijerG:

FoxH representation of the LommelS1 function:

Applications (1)

Solve the inhomogeneous Bessel equation:

Properties & Relations (2)

Use FunctionExpand to expand LommelS1 into hypergeometric functions:

FunctionExpand for a specific set of parameters can generate simpler special functions:

Neat Examples (1)

Riemann surface of LommelS1:

Top