MatrixForm

MatrixForm[list]

用来输出 list 的元素，这些元素以一个规则阵列排列.

更多信息和选项

  • 在 StandardForm 中，该阵列被放入括号内显示.
  • MatrixForm 以一个列的形式输出单层次列表. 它以标准矩阵形式输出一个二层次列表. 更深层次的嵌套列表在默认情况下与在行列之间变化的连续维数一起被输出.
  • 每一列的元素在默认情况下被放在中央.
  • MatrixForm 输出 SparseArray 对象，如相应的普通列表一样. »
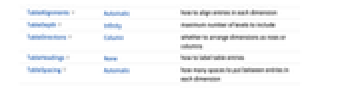
  • MatrixForm 有与 TableForm 相同的可选项.
  • 作为输入时，MatrixForm[expr] 的排版形式被解释为与 expr 一样. »
  • 当输入的运算结果为 MatrixForm[expr] 时，MatrixForm 不会出现在输出中. »

    • 所有选项的列表

范例

打开所有单元关闭所有单元

基本范例  (3)

显示一个矩阵的矩阵形式：

显示一个 SparseArray 的矩阵形式：

以矩阵的形式显示矢量、矩阵和一般数组：

范围  (3)

数字和公式矩阵：

列表矩阵：

使用选项来控制布局方向：

推广和延伸  (2)

将 SparseArray 对象格式化为矩阵形式：

将 SymmetrizedArray 对象格式化为矩阵形式：

选项  (6)

TableAlignments  (2)

指定列的对齐：

设置连续维度上如何对齐：

TableDepth  (1)

默认情况下，所有维度都被格式化：

仅在最外面的维度使用矩阵格式：

TableDirections  (1)

默认情况下，最外维是一列：

格式化第一维为一行：

TableHeadings  (1)

指定行的标题：

指定列的标题：

指定行和列的标题：

TableSpacing  (1)

默认自动间距：

明确指定行和列之间的间距：

应用  (4)

用矩阵格式显示特殊矩阵：

矩阵分解得到的矩阵：

矩阵乘法公式：

显示一个分块矩阵为矩阵的矩阵：

数组压平为矩阵：

属性和关系  (7)

MatrixForm 使用标准矩阵格式来格式化数组：

TableForm 以表格形式格式化数组：

Grid 格式化二维数组为一网格：

使用 MatrixPlot 来显现大型矩阵的结构：

使用 ArrayPlot 来显现大型离散矩阵的结构：

使用 Style 来影响 MatrixForm 的显示：

使用任何数字形式如 ScientificForm 或 BaseForm 来影响数字的显示：

作为输入时，MatrixForm[expr] 的排版形式被解释为与 expr 一样：

复制输出，将其粘贴到输入单元. (

12
34
) 被解释为 {{1,2},{3,4}}：

当输入的运算结果为 MatrixForm[expr] 时，MatrixForm 不会出现在输出中：

赋给 Out 的值是 {{1,2},{3,4}}，不是 MatrixForm[{{1,2},{3,4}}]：

可能存在的问题  (1)

即便输出省略了上一层的 MatrixForm，子表达式中依然存在：

输出中没有 MatrixForm：

但是，变量 e 含有 MatrixForm，可能会影响后续的计算：

由于 MatrixForm 的存在，不能计算行列式：

先对变量赋值，然后对结果应用 MatrixForm，使计算可以进行：

Wolfram Research (1988)，MatrixForm，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MatrixForm.html （更新于 2003 年）.

文本

Wolfram Research (1988)，MatrixForm，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MatrixForm.html （更新于 2003 年）.

CMS

Wolfram 语言. 1988. "MatrixForm." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2003. https://reference.wolfram.com/language/ref/MatrixForm.html.

APA

Wolfram 语言. (1988). MatrixForm. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixForm.html 年

BibTeX

@misc{reference.wolfram_2024_matrixform, author="Wolfram Research", title="{MatrixForm}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixForm.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_matrixform, organization={Wolfram Research}, title={MatrixForm}, year={2003}, url={https://reference.wolfram.com/language/ref/MatrixForm.html}, note=[Accessed: 05-November-2024 ]}