MaxValue

MaxValue[f,x]

x についての f の最大値を与える．

MaxValue[f,{x,y,…}]

x, y, …についての f の最大値を与える．

MaxValue[{f,cons},{x,y,…}]

制約条件 cons の下での f の最大値を与える．

MaxValue[…,x∈rdom]

x が領域 rdom 内にあるように制限する．

MaxValue[…,…,dom]

変数を領域 dom（一般にRealsまたはIntegers）に制限する．

詳細とオプション

  • MaxValueは上限（シュープレマム）としても知られている．
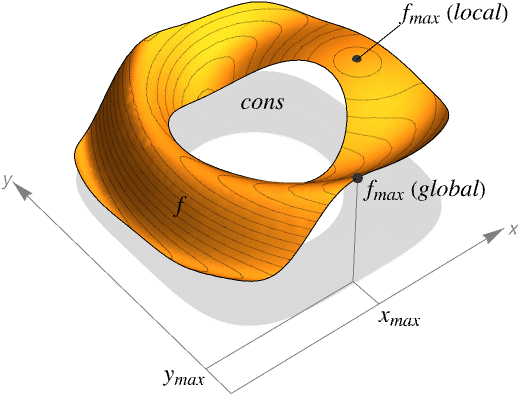
  • MaxValueは与えられた制約条件に従って f の最大値を求める．
  • MaxValueは，通常，制約条件下で可能な最大値を求めるために使われる．分野によっては，最適な戦略，最良適合，最適な構成等と呼ばれることがある．
  • Maximizeは{fmax,{x->xmax,y->ymax,…}}の形式のリストを返す．
  • f および cons が線形あるいは多項式の場合，MaxValueは常に大域的な上限を求める．
  • 制約条件 cons は以下の任意の論理結合でよい．
  • lhs==rhs等式
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs不等式 (LessEqual,…)
    lhsrhs, lhsrhs, lhsrhs, lhsrhsベクトル不等式 (VectorLessEqual,…)
    Exists[…], ForAll[…]量化条件
    {x,y,…}∈rdom領域指定
  • MaxValue[{f,cons},x∈rdom]は，事実上，MaxValue[{f,cons∧x∈rdom},x]に等しい．
  • x∈rdom については，Indexed[x,i]を使って別の座標に言及することができる．
  • 次は，使用可能な領域 rdom である．
  • Reals実数スカラー変数
    Integers整数スカラー変数
    Vectors[n,dom]のベクトル変数
    Matrices[{m,n},dom]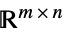の行列変数
    ℛ幾何領域 に制限されたベクトル変数
  • デフォルトで，すべての変数が実数であるとみなされる．
  • MaxValueは入力が厳密値の場合は厳密値を返す．入力が近似値の場合は自動的にNMaxValueを呼び出す．
  • MaxValueは次の形式を返す．
  • fmax有限最大値
    -∞実行不可能，つまり，制約条件集合が空
    ∞非有界，つまり，f の値は任意に大きくできる
  • MaxValueは f の値の最小上界を与える．これは，x, y, …のいずれの値についても達成できない可能性がある．
  • N[MaxValue[…]]は，記号的には解けない最適化問題についてはNMaxValueを呼び出す．

例題

すべて開くすべて閉じる

例  (5)

一変数関数の最大値を求める：

多変数関数の最大値を求める：

制約条件のもとでの関数の最大値を求める：

最大値をパラメータの関数として求める：

幾何学領域上で関数の最大値を求める：

スコープ  (36)

基本的な用法  (7)

制約条件のない実数上でを最大にする：

制約条件 に従って を最大にする：

制約条件は任意の論理結合を含むことがある：

非有界の問題：

実行不可能な問題：

上限値には達しないかもしれない：

ベクトル変数とベクトル不等式を使う：

一変数の問題  (7)

制約条件なしの一変数多項式の最大化：

制約条件付きの一変数多項式の最大化：

指数対数関数：

有界の条件上での解析関数：

周期関数：

三角関数と通約可能な周期の組合せ：

周期関数と通約可能な周期の組合せ：

区分関数：

関数の特性情報を使って可解の制約条件がない問題：

多変数の問題  (9)

多変数線形制約条件付き最大化：

線形分数制約条件付き最大化：

制約条件なしの多項式の最大化：

制約条件付き多項式の最適化は常に解くことができる：

最大値には達しないことがあるかもしれない：

目的関数は有界ではないかもしれない：

制約条件を満足する点は存在しないかもしれない：

定量化された多項式制約：

代数的最大化：

有界超越関数の最大化：

区分関数の最大化：

凸最大化：

が半正定でとなるように凹目的関数を最大にする：

関数と最大値を領域上にプロットする：

パラメトリック問題  (4)

パラメトリック線形最適化：

最大値はパラメータの連続関数である：

パラメトリック二次最適化：

最大値はパラメータの連続関数である：

制約条件なしのパラメトリック多項式最大化：

制約条件付きのパラメトリック多項式最大化：

整数上の最適化  (3)

一変数問題：

整数線形計画法：

整数上における多項式の最大化：

領域上の最適化  (6)

幾何学領域上で関数の最大値を求める：

これをプロットする：

2領域中の点の最大距離を求める：

三角形と楕円が交差する の最大値を求める：

これをプロットする：

に指定された3点が含まれる の最大値を求める：

を使って が中のベクトルであると指定する：

2領域内の点の最大距離を求める：

オプション  (1)

WorkingPrecision  (1)

厳密な最大値を求めるのには時間がかかる：

WorkingPrecision->200とすると，厳密な最大値を求めることはできるが，結果は正しくないかもしれない：

アプリケーション  (13)

基本的なアプリケーション  (4)

単位周長の長方形で面積が最大のものを求める：

単位周長の三角形で面積が最大のものを求める：

投射物で高さが最大のものを求める：

投射物の最大範囲を求める：

関数 f[x] の無限ノルムはMaxValue[{Norm[f[x]],x∈},x]で与えられる．ただし， は f[x]についての関心領域である．区間{-3,3}についての の無限ノルムを求める：

プロットする：

についての無限ノルムをRectangle[{-1,-1},{1,1}]上で求める：

プロットする：

幾何学的距離  (9)

領域 ℛ 内の点から指定された点 p までの最大距離はMaxValue[EuclideanDistance[p,q],q∈ℛ]で与えられる．単位Disk[]内の点から{1,1}までの最大距離を求める：

これをプロットする：

標準的な単位シンプレックスSimplex[2]内の点から点{1,3/4}までの最大距離を求める：

これをプロットする：

標準的な単位球Sphere[]内の点から{1,1,1}までの最大距離を求める：

これをプロットする：

標準的な単位シンプレックスSimplex[3]内の点から点{-1/3,1/3,1/3}までの最大距離を求める：

これをプロットする：

領域 ℛ の直径は ℛ 内の2点の最大距離であり，MaxValue[EuclideanDistance[p,q],{p∈ℛ,q∈ℛ}]で計算することができる．Circle[]の直径を求める：

標準的な単位シンプレックスSimplex[2]の直径を求める：

標準的な単位立方体Cuboid[]の直径を求める：

点 p∈ と q∈ 野最大距離はMaxValue[EuclideanDistance[p,q],{p∈,q∈}]で求めることができる．Disk[{0,0}]内の点とRectangle[{3,3}]内の点の最大距離を求める：

Line[{{0,0,0},{1,1,1}}]内の点とBall[{5,5,0},1]内の点の最大距離を求める：

特性と関係  (4)

Maximizeは最大値と最大となる点の両方を与える：

MaxValueは目的関数の厳密な最大値を与える：

NMaxValueは最大値を数値的に求めようとするが，求まるのは極大値のことがある：

FindMaxValueは始点によって極大値を求める：

MaxValueは線形計画法問題を解くことができる：

LinearProgrammingは行列表記で与えられた同じ問題を解くのに使うことができる：

RegionBoundsを使って境界ボックスを計算する：

MaxValueおよびMinValueを使って同じ境界を計算する：

考えられる問題  (1)

MaxValueは入力中のすべての関数が実数値であることを必要とする：

方程式は満たすが平方根が実数ではない値は許容されない：

Wolfram Research (2008), MaxValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/MaxValue.html （2021年に更新）.

テキスト

Wolfram Research (2008), MaxValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/MaxValue.html （2021年に更新）.

CMS

Wolfram Language. 2008. "MaxValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/MaxValue.html.

APA

Wolfram Language. (2008). MaxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaxValue.html

BibTeX

@misc{reference.wolfram_2024_maxvalue, author="Wolfram Research", title="{MaxValue}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/MaxValue.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maxvalue, organization={Wolfram Research}, title={MaxValue}, year={2021}, url={https://reference.wolfram.com/language/ref/MaxValue.html}, note=[Accessed: 14-November-2024 ]}