NewMoon
NewMoon[]
gives the date of the next new moon.
NewMoon[date]
gives the date of the first new moon after the given date.
Details and Options
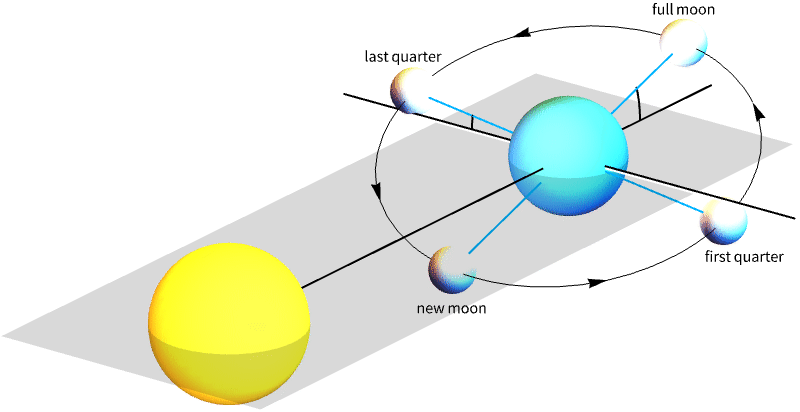
- The instant of new moon is defined by the conjunction of the Moon and the Sun in ecliptic longitude.
- In NewMoon[date], date can be any DateObject expression.
- Options of NewMoon include:
-
CalendarType Automatic calendar used to return dates DateFormat Automatic format used to display output dates DateGranularity Automatic calendar granularity of output dates Method "EclipticLongitude" method to define moon phases TimeDirection 1 whether to return the next or last new moon TimeSystem Automatic time system of output dates TimeZone $TimeZone time zone of output dates - Possible settings for the Method option include:
-
"Illumination" phase defined by fraction of illumination of the Moon "EclipticLongitude" phase defined by Moon‐Sun ecliptic longitude difference
Examples
open allclose allBasic Examples (2)
Scope (3)
Options (7)
CalendarType (1)
NewMoon returns dates in the Gregorian calendar by default:
DateFormat (1)
NewMoon returns dates in a long format by default:
DateGranularity (1)
NewMoon returns dates with granularity "Instant" by default:
Method (1)
NewMoon uses differences of ecliptic longitudes between the Sun and the Moon by default:
Use the minimum value of illumination to define the instant of new moon instead:
TimeDirection (1)
NewMoon finds the next new moon by default:
TimeSystem (1)
NewMoon returns dates in universal time by default:
TimeZone (1)
NewMoon returns dates in your local time zone by default:
Applications (1)
Properties & Relations (7)
At the instant of new moon, the Moon and the Sun have the same ecliptic longitude:
The distance between new moons is called a synodic month, and varies between 29.26 and 29.80 days:
The average synodic month is about 29.53 days:
NewMoon returns the date of the next new moon:
Use FullMoon to find the date of the next full moon, which may be before or after that new moon:
Use MoonPhaseDate to find the date of any phase of the Moon:
MoonPhase computes the phase fraction of illumination, which is close to zero for a new moon:
The minimum of illumination is given by this alternative method of computation:
This curve represents fraction of illumination for an hour around the minimum, with newmoon in red:
New moons correspond to integer lunation numbers:
Therefore, an alternative way of finding new moons is calling FromLunationNumber with integers:
New moons are conjunctions of the Moon with the Sun, as observed from the center of the Earth:
Every solar eclipse happens within a few minutes of a new moon:
Only 2 to 5 of the 12 or 13 new moons in a year are close to solar eclipses:
Text
Wolfram Research (2024), NewMoon, Wolfram Language function, https://reference.wolfram.com/language/ref/NewMoon.html (updated 2025).
CMS
Wolfram Language. 2024. "NewMoon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/NewMoon.html.
APA
Wolfram Language. (2024). NewMoon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NewMoon.html