MoonPhaseDate

MoonPhaseDate[]

returns the date of the next new moon.

MoonPhaseDate[phase]

returns the date of the next instance of the given phase of the Moon.

MoonPhaseDate[date,phase]

returns the date for the first instance of the given phase after date.

Details and Options

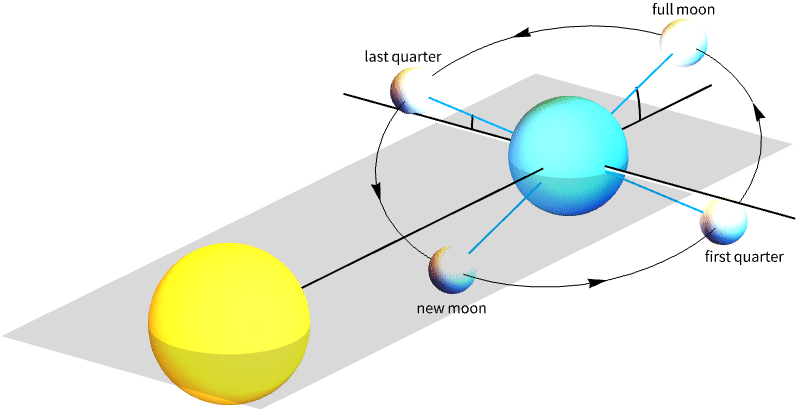
  • The phase of the Moon describes the angle between the Moon and Sun, which determines the apparent shape of the Moon, as observed from the Earth.
  • MoonPhaseDate reports dates of new moons, full moons or any other phase of the Moon.
  • In MoonPhaseDate[phase], the phase can be given as a named case, such as "NewMoon" or "FirstQuarter", an entity such as Entity["MoonPhase","New"], or as a continuous real number with value 0 for a new moon, 0.25 for the first quarter, 0.5 for a full moon, 0.75 for the last quarter and 1 for the following new moon.
  • Special named cases of full moons include:
  • "SeasonalBlueMoon"third full moon in a season with four full moons
    "MonthlyBlueMoon"second full moon in a month with two full moons
    "HarvestMoon"full moon nearest to the September equinox
    "HuntersMoon"full moon following the harvest moon
  • In MoonPhaseDate[date,phase], date can be any DateObject expression.
  • Options of MoonPhaseDate include:
  • CalendarType Automaticcalendar used to return dates
    DateFormat Automaticformat used to display output dates
    DateGranularity Automaticcalendar granularity of output dates
    Method "EclipticLongitude"method to define moon phases
    TimeDirection 1whether to return the next or last date of a given phase
    TimeSystem Automatictime system of output dates
    TimeZone $TimeZonetime zone of output dates
  • Possible settings for the Method option include:
  • "Illumination"phase defined by fraction of illumination of the Moon
    "EclipticLongitude"phase defined by Moon‐Sun ecliptic longitude difference

Examples

open allclose all

Basic Examples  (3)

Find the date of the next new moon:

Find the date of the next first quarter:

Find the date of the first new moon after January 1, 2000:

Scope  (5)

Specify the same phase of the Moon in different ways:

Find the next seasonal blue moon:

Such a full moon will be the third of four full moons in a season:

Find the next monthly blue moon:

Such a full moon will be the second in the same month, as defined by your local time zone:

Find the next harvest moon:

The full moon following about one month later is called the hunter's moon:

Find the date of a given phase of the Moon after some date:

Options  (7)

CalendarType  (1)

MoonPhaseDate returns dates in the Gregorian calendar by default:

Return dates in the Jewish calendar:

DateFormat  (1)

MoonPhaseDate returns dates in a long format by default:

Specify your own format:

DateGranularity  (1)

MoonPhaseDate returns dates with granularity "Instant" by default:

Return dates with "Day" granularity:

Method  (1)

MoonPhaseDate uses differences of ecliptic longitudes between the Sun and the Moon by default:

Use a value of illumination to define the instant of a given moon phase:

TimeDirection  (1)

MoonPhaseDate finds the next new moon by default:

Find the previous new moon:

TimeSystem  (1)

MoonPhaseDate returns dates in universal time by default:

Return dates in "TT" time instead:

TimeZone  (1)

MoonPhaseDate returns dates in your local time zone by default:

Return dates in the GMT time zone:

Properties & Relations  (6)

At every new moon, the Sun and the Moon have the same ecliptic longitude:

There will be a solar eclipse if the difference in ecliptic latitude is small enough:

MoonPhaseDate gives the date of a given phase of the Moon:

MoonPhase gives illumination fractions and names:

Entity phases can also be used in MoonPhaseDate:

Use the "Illumination" method to find when 50% of the surface of the Moon appears illuminated:

NewMoon is the particular case of MoonPhaseDate for new moons:

FullMoon is the particular case of MoonPhaseDate for full moons:

New moons are conjunctions of the Moon with the Sun:

Full moons are oppositions of the Moon with respect to the Sun:

First quarters are eastern quadratures of the Moon with respect to the Sun:

Last quarters are western quadratures of the Moon with respect to the Sun:

Find the date of a random Moon phase value p:

This date can also be obtained using FromLunationNumber, using p as the decimal part of the current integer lunation number:

Wolfram Research (2024), MoonPhaseDate, Wolfram Language function, https://reference.wolfram.com/language/ref/MoonPhaseDate.html (updated 2025).

Text

Wolfram Research (2024), MoonPhaseDate, Wolfram Language function, https://reference.wolfram.com/language/ref/MoonPhaseDate.html (updated 2025).

CMS

Wolfram Language. 2024. "MoonPhaseDate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/MoonPhaseDate.html.

APA

Wolfram Language. (2024). MoonPhaseDate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MoonPhaseDate.html

BibTeX

@misc{reference.wolfram_2024_moonphasedate, author="Wolfram Research", title="{MoonPhaseDate}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MoonPhaseDate.html}", note=[Accessed: 20-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2024_moonphasedate, organization={Wolfram Research}, title={MoonPhaseDate}, year={2025}, url={https://reference.wolfram.com/language/ref/MoonPhaseDate.html}, note=[Accessed: 20-January-2025 ]}