Norm

Norm[expr]

给出一个数字、向量或矩阵的模（范数）.

Norm[expr,p]

给出 ‐范数.

更多信息和选项

空模板可以通过按下 norm 输入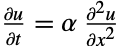，可以通过按下 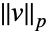norm2 输入. »
Norm[expr] 格式化为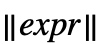，而 Norm[expr,p] 格式化为 . »
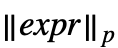对于复数来说，Norm[z] 就是 Abs[z].
对于向量来说，Norm[v] 就是 Sqrt[v.Conjugate[v]]. »
对于向量来说，Norm[v,p] 在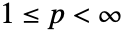时为 Total[Abs[v]^p]^(1/p).
对于向量来说，Norm[v,Infinity] 是 Max[Abs[v]] 给出的 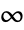‐范数. »
对于矩阵，Norm[m] 返回谱范数或算子范数，即 m 的最大奇异值. »
矩阵的范数规范包括：

	1	诱导 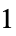-范数，算子 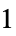-范数
	2	谱范数，算子范数
	Infinity	诱导 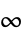-范数，算子 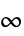-范数
	"Frobenius"	Frobenius 范数或 Hilbert–Schmidt 范数

矩阵的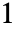范数是其各列的 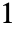-范数中的最大值，而该矩阵的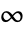范数是其各行的 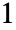-范数中的最大值. »
Frobenius 范数计算由矩阵 m 的各个元素组成的向量的 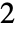-范数，即 Norm[Flatten[m]]. »
Norm 可用于 SparseArray 和结构化数组对象. »

范例

打开所有单元关闭所有单元

基本范例 (3)

二维向量的范数：

三维向量的范数：

复数的模（范数）：

范围 (16)

向量 (7)

符号向量的范数：

化简，假设各项为实数：

复值向量的范数：

有限 -范数：

-范数：

使用非整数计算范数：

v 是一个整数向量：

使用精确算术来计算范数：

使用近似的机器数值计算：

使用 35 位数值精度运算：

结构化向量的范数：

维度为 20 的稀疏向量的 -范数：

矩阵 (6)

矩阵的范数，等于最大的奇异值：

实参数的符号矩阵范数：

当范数在没有实数假设的情况下计算时，结果会复杂得多：

矩阵的 -范数是该矩阵各列的 -范数的最大值：

矩阵的 -范数是该矩阵各行的 -范数的最大值：

矩阵的 Frobenius 范数：

结构化矩阵的范数：

单位矩阵的三种诱导范数是相同的：

Frobenius 范数是不同的，其值等于维数的平方根：

以 SparseArray 对象表示的三对角矩阵的谱范数：

格式化 (3)

输入 norm 以创建模板，然后输入一个向量以计算其范数：

输入 norm2 以插入模板；按下在各位置间切换：

输出格式：

Frobenius 范数有专门的格式：

应用 (3)

在单位面积里，估计从原点到随机点的平均距离：

与渐近线的结果相比较：

用一个已知的解，求解一个病态线性系统：

得到余范数：

得到实际误差的范数：

使用个空间点和时间步长求函数的近似解：

找到两个带有固定的的解，第二个有两倍的时间步长：

通过计算差异范数，估计误差：

从反向欧拉方法的一阶收敛外推导出一个较好的解：

用 NDSolve 计算更精确的答案：

比较三个答案的误差：

属性和关系 (7)

范数始终为非负数：

v 的范数与 Dot 和乘积的平方根相等：

对于向量，默认范数为 2-范数：

矩阵也是如此：

是的减函数：

极限值为范数，等于 Max[Abs[v]]：

对于所有单位向量 v 来说，矩阵 -范数是 m.v 的 -范数的最大值：

这个与的最大奇异值相等：

Frobenius 范数与元素向量生成的范数是一样的：

对于矩阵 m，Norm[m,Infinity] 可以计算为 Max[Total/@Abs/@m]：

这相当于计算每一行的-范数，并取其最大值：

Norm[m,1] 可以通过 Max[Total/@Abs/@Transpose[m]] 计算得到：

这相当于计算各列的-范数并取最大值：

可能存在的问题 (2)

计算大型矩阵的 -范数，比较费时：

如果你只需要估计，-范数或者 -范数是非常快的：

一般向量的范数包含 Abs：

使用 Simplify 和 FullSimplify 可以在假设参数为实数的情况下得到更简洁的结果：

巧妙范例 (2)

使用 1、2、3 和范数的单位球：

不同的范数函数：

Top

更多学习资源

技术支持

Wolfram 解决方案

Wolfram 的教育解决方案

开始

提高你的技能

与我们合作

成人教育计划

青少年教育计划

欢迎阅读

Norm

更多信息和选项

范例

基本范例 (3)