Point

Point[p]

是一个图形和几何基元，表示位于 p 的一个点.

Point[{p1,p2,…}]

表示一些点的集合.

更多信息和选项

背景

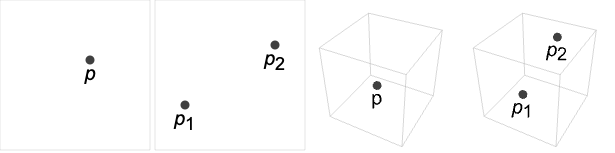
  • Point 是表示几何点的图形及几何基元. Point 在 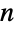维空间中的位置是由 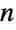个笛卡尔坐标值组成的列表参数指定的，其中 RegionEmbeddingDimension 可被用于确定给定 Point 表达式的维度 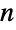. 一组点可被表示为单个 Point 基元中的 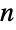元组列表（“众点”）. Point 对象的坐标可以是精确值或近似值.
  • 可以分别用 Graphics 和 Graphics3D 在二维和三维空间中显示 Point 对象. Point 对象也可以通过 GeoGraphics 和 GeoPosition 用在地理地图中（例如 GeoGraphics[Point[GeoPosition[{38.9,-77.0}]]]）. 最后，也可以用 Point 来定义需要进行计算的区域.
  • 尽管点自身的维度是 0（见 RegionDimension 函数的返回结果），在格式化的图形表达式的默认输出中，Point 对象显示得要比 0 维的数学上的点要“大”些. 而且在图形可视化中，不管从哪个角度看，距离有多远，图形中点的大小不变. 如果想要改变 Point 对象的样式，可以使用调整大小的指令，如 PointSize 和 AbsolutePointSize；着色指令，比如 Red；规定透明度的指令 Opacity；以及样式选项 Antialiasing. 此外，可以用 VertexColors 指定众点的颜色，而众点在 Graphics3D 中的阴影和模拟光照则可使用 VertexNormals 指令来指定.
  • 我们可以使用 GeometricTransformation 和更具体的转换函数，比如 Translate 和 Rotate，来改变图形输出中 Point 对象所在的坐标，但保持产生该输出的 Point 表达式不变.
  • 其他图形基元，如 Circle、Disk、Sphere 及 Ball 和样式经过调整的 Point 对象类似. Locator 是另一个和点类似的交互式对象，它可用在图形中代表一个可拖拽的定位器对象.
  • 尽管 Point 基元可以出现在图形和定义几何区域的表达式中，但要注意到，在 Wolfram 语言里，其他情况下坐标通常都以纯列表形式表示. 这种类型的例子包括出现在其他图形基元中的坐标设定（例如 Line[{{0, 0},{1,1}}]），Locator 的参数（例如 Graphics[Locator[{0,2}]]），以及当使用 Nearest 计算最接近的点时. 许多函数（包括 RegionNearest、RegionCentroid、ArgMin 和 ArgMax）也自然的返回坐标的纯列表形式而不是显式的 Point 对象，而其它函数（例如 Solve 和 NSolve）则以变量替换规则列表的形式返回解的“点”（例如 ）.

范例

打开所有单元关闭所有单元

基本范例  (5)

单个点：

多个点：

在三维图形中的点：

不同样式的点：

计算点的数量和几何中心：

范围  (20)

图形  (10)

规范  (2)

单个点：

多个点：

样式  (5)

不同大小的点：

大小成比例的点：

用打印机阵点来指定点的大小：

有颜色的点：

用 VertexColors 来指定顶点的颜色：

用 VertexNormals 来指定三维点顶点处的法线：

坐标  (3)

使用 Scaled 坐标：

在二维图形中使用 ImageScaled 坐标：

在二维图形中使用 Offset 坐标：

区域  (10)

嵌入维度是点所处空间的维度：

点的几何维度是0：

判断某点是否为该区域的成员：

获取成为该区域成员的条件：

一个集合的点的度量是计数度量：

几何中心：

到点的集合的距离：

距一个点的有符号距离：

区域中最近的点：

最近的点：

点的集合是有界的：

边界范围：

用计数度量在由三个点组成的集合上 Integrate：

一种等价的方法：

在由三个点组成的集合上最优化：

在由1000个点组成的集合上解方程：

选项  (3)

VertexColors  (2)

带有颜色的点：

指定三维点的颜色：

VertexNormals  (1)

指定三维点的顶点法线：

应用  (5)

用 Point 表示特殊的点，例如函数的零点：

简单的将点分类，用 Point 来可视化：

在三维中将点分类：

显示聚类分析的结果：

可以用 Point 来取代 Polygon 来达到特殊的渲染效果：

属性和关系  (2)

用 ListPlot 显示一维序列：

用 ListPointPlot3D 显示二维序列：

可能存在的问题  (1)

PointSize 按图形的宽度缩放大小：

用 AbsolutePointSize 控制大小：

巧妙范例  (3)

一个随机点的集合：

单位球面上带有正确法线的点：

从移动的中心出发分散网格点：

Wolfram Research (1988)，Point，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Point.html （更新于 2014 年）.

文本

Wolfram Research (1988)，Point，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Point.html （更新于 2014 年）.

CMS

Wolfram 语言. 1988. "Point." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/Point.html.

APA

Wolfram 语言. (1988). Point. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Point.html 年

BibTeX

@misc{reference.wolfram_2024_point, author="Wolfram Research", title="{Point}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Point.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_point, organization={Wolfram Research}, title={Point}, year={2014}, url={https://reference.wolfram.com/language/ref/Point.html}, note=[Accessed: 21-November-2024 ]}