Point

Point[p]

is a graphics and geometry primitive that represents a point at p.

Point[{p1,p2,…}]

represents a collection of points.

Details and Options

Background & Context

  • Point is a graphics and geometry primitive that represents a geometric point. The position of a Point in 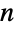-dimensional space is specified as a list argument consisting of 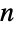Cartesian coordinate values, where RegionEmbeddingDimension can be used to determine the dimension 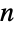for a given Point expression. A collection of points may be represented as a list of 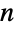-tuples inside a single Point primitive (a "multi-point"). The coordinates of Point objects may have exact or approximate values.
  • Point objects can be visually formatted in two and three dimensions using Graphics and Graphics3D, respectively. Point objects can also be used in geographical maps using GeoGraphics and GeoPosition (e.g. GeoGraphics[Point[GeoPosition[{38.9,-77.0}]]]). Finally, Point may serve as a region specification over which a computation should be performed.
  • While points themselves have dimension 0 (as reported by the RegionDimension function), Point objects in formatted graphics expressions are by default styled to appear "larger" than a 0-dimensional mathematical point. Furthermore, in graphical visualizations, points are displayed at the same size regardless of possibly differing distances from the view point. The appearance of Point objects in graphics can be modified by specifying sizing directives such as PointSize and AbsolutePointSize, color directives such as Red, the transparency directive Opacity, and the style option Antialiasing. In addition, the colors of multi-points may be specified using VertexColors, while the shading and simulated lighting of multi-points within Graphics3D may be specified using VertexNormals.
  • GeometricTransformation and more specific transformation functions such as Translate and Rotate can be used to change the coordinates at which a Point object is displayed while leaving the underlying Point expression untouched.
  • Other graphics primitives such as Circle, Disk, Sphere, and Ball may resemble those of stylized Point objects. Locator is another point-like interactive object that represents a draggable locator object in a graphic.
  • While the Point primitive explicitly appears in graphics and geometric region specification expressions, it should be noted that coordinates are commonly represented as bare lists in other contexts in the Wolfram Language. Examples of this type include coordinate specifications appearing inside other graphics primitives (e.g. Line[{{0, 0},{1,1}}]), arguments to Locator (e.g. Graphics[Locator[{0,2}]]), and when using Nearest to compute a nearest point. A number of functions (e.g. RegionNearest, RegionCentroid, ArgMin, and ArgMax) also naturally return bare lists of coordinates as opposed to explicit Point objects, while others (e.g. Solve and NSolve) return solution "points" as lists of variable replacement rules (e.g. ).

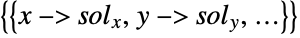Examples

open allclose all

Basic Examples  (5)

A single point:

Multiple points:

Points in 3D:

Differently styled points:

Count and centroid:

Scope  (20)

Graphics  (10)

Specification  (2)

A single point:

Multiple points:

Styling  (5)

Points with different sizes:

Scaled point size:

Point size in printer's points:

Colored points:

Colors can be specified at vertices using VertexColors:

Normals can be specified at vertices using VertexNormals for 3D points:

Coordinates  (3)

Use Scaled coordinates:

Use ImageScaled coordinates in 2D:

Use Offset coordinates in 2D:

Regions  (10)

Embedding dimension is the dimension in which the points live:

The geometric dimension of a point is always 0:

Point membership test:

Get conditions for point membership:

The measure of a set of points is the counting measure:

Centroid:

Distance to a set of points:

Signed distance from a point:

Nearest point in the region:

Nearest points:

A point set is bounded:

The bounding range:

Integrate over a three-point set using the counting measure:

An equivalent way:

Optimize over a three-point set:

Solve equations in a 1000-point set:

Options  (3)

VertexColors  (2)

Point with vertex colors:

Specify vertex colors for 3D points:

VertexNormals  (1)

Specify vertex normals for 3D points:

Applications  (5)

Use Point to indicate features, e.g. zeros of a function:

A simple point classification, visualized using Point:

The same idea in 3D:

Visualize the result of cluster analysis:

Replace Polygon with Point to have special rendering effects:

Properties & Relations  (2)

Use ListPlot to visualize 1D sequences:

Use ListPointPlot3D to visualize 2D sequences:

Possible Issues  (1)

PointSize is a scaled size that refers to the width of the graphic:

Use AbsolutePointSize to control the size:

Neat Examples  (3)

A random point collection:

Points on the unit sphere with correct normals:

Disperse a grid of points from a moving center:

Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).

Text

Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).

CMS

Wolfram Language. 1988. "Point." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Point.html.

APA

Wolfram Language. (1988). Point. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Point.html

BibTeX

@misc{reference.wolfram_2024_point, author="Wolfram Research", title="{Point}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Point.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_point, organization={Wolfram Research}, title={Point}, year={2014}, url={https://reference.wolfram.com/language/ref/Point.html}, note=[Accessed: 21-November-2024 ]}