PoissonPointProcess

PoissonPointProcess[μ,d]

における一定強度 μ の同次ポアソン(Poisson)点過程を表す．

詳細

  • PoissonPointProcessは，同次ポアソン点過程，定常ポアソン点過程，完全空間ランダム性(CSR)としても知られている．
  • PoissonPointProcessは，単位体積あたりの点の平均数が μ に等しい，領域内の一様分布に従う点を生成する．
  •     
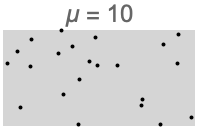
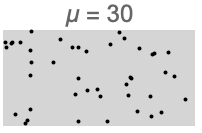
  • この過程は，完全に空間的にランダムな点集合のモデル化とテストによく使われ，クラスタ化された点過程等のより複雑な点過程の構成要素としても頻繁に利用される．
  • 強度が μ のとき，体積が 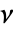の観測領域内の点の数は分布PoissonDistribution[μ ν]に従う．
  • ポアソン点過程では，互いに素な領域 内の点の数 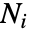は独立乱数からなるので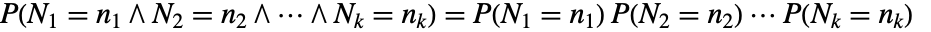，である．この特性は完全空間ランダム性(CSR)としても参照される．
  • 体積が の観測領域 内の強度 μ の配置の密度関数は，PoissonPointProcess[1,d]について である．
  • 点 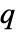を点集合に加えるPapangelou条件密度 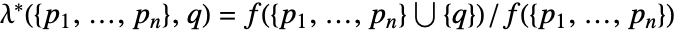は，強度 μ のポアソン点過程について 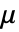である．
  • PoissonPointProcessでは，μ は任意の正の実数でよく，d は任意の正の整数でよい．
  • 次は，EstimatedPointProcessにおけるPoissonPointProcessについてのPointProcessEstimatorの可能な設定である．
  • Automaticパラメータ推定器を自動選択する
    "MaximumPseudoLikelihood"擬似尤度を最大にする
  • PoissonPointProcessは，RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (3)

ポアソン点過程からサンプルを取る：

いくつかの実現があるポアソン点過程からサンプルを取る：

国の上でポアソン点過程のシミュレーションを行う：

スコープ  (4)

RegionEmbeddingDimensionがそのRegionDimensionと等しい任意の有効な領域からポアソン点過程のサンプルを取る：

領域の条件をチェックする：

領域から点のサンプルを取る：

別のメソッドを使ってPoissonPointProcessからサンプルを取る：

細線化法を使う：

マルコフ(Markov)鎖モンテカルロ法：

サンプルを領域上にプロットする：

PoissonPointProcessを推定する：

PoissonPointProcessを地理領域上で推定する：

メートル法に変換する：

PointCountDistributionを求める：

地理的なケースについて：

アプリケーション  (3)

合板の欠陥が50平方フィートあたり平均1つ発生するとする．1平方フィートごとに欠陥を見付ける過程のシミュレーションを行う：

4フィート × 8フィートの合板に欠陥がある確率を求める：

面積が7.54cm^2の丸い鏡に欠陥がない確率は0.91である．同じ研磨過程を用いて19.50cm^2の面積を持つ別の丸い鏡が製造される．欠陥が独立でランダムに分布するものと仮定して，大きな鏡に欠陥がない確率を求める：

欠陥点過程の強度を求める：

結果の鏡面研磨欠陥過程は以下のようになる：

大きい鏡に欠陥がない確率：

1920×1080画素のLCDディスプレイがある．問題のある画素が15個以下の場合，ディスプレイは受領される．画素に生産による欠陥がある確率はであり，欠陥のある画素位置は独立でランダムである．受領されるディスプレイの割合を求める：

問題がある画素配置のシミュレーションを行う：

ディスプレイの問題がある画素数が15個未満である確率を求める：

4000画素×2000画素のディスプレイを作成し，それでも少なくとも90％の受領率を維持するために必要な画素欠陥率を求める：

受領率を画素欠陥率の関数としてプロットする：

受領される最大画素欠陥率を求める：

結果をチェックする：

特性と関係  (11)

PoissonPointProcess内の点の数はポアソン分布に従っている：

単位円板上でPoissonPointProcessのシミュレーションを行う：

点の数の分布：

点の数のヒストグラムを確率密度関数と比較する：

PoissonDistributionを点の数にフィットする：

適合度を調べる：

もとになっている分布に対して調べる：

円板についてポアソン点過程のボイド確率を計算する：

長方形について：

単位球について：

任意の場所から距離 内にある点が見付かる確率：

RayleighDistributionのCDFとの等価性：

同様に，PointCountDistributionの0におけるSurvivalFunctionを計算する：

ポアソン点過程は定常で，強度は並進不変である：

部分領域における点の数の分布：

並進部分領域における点の数の分布：

ポアソン点過程は等方性で，強度は原点の周りの回転において不変である：

部分領域における点の数の分布：

並進部分領域における点の数の分布：

PoissonPointProcessは完全空間ランダム性という特性を持つ：

左と右の半円を定義する：

各部分領域における点の部分集合を作る：

各部分領域の点の数を抽出する：

2つのサンプルが独立かどうかを調べる：

ポアソン点過程についてのRipleyの 関数は閉じた形を持ち，強度に依存しない：

いくつかの次元について関数をプロットする：

ポアソン点過程についてのBesagの 関数は強度や次元性に依存しない：

ポアソン点過程についてのPairCorrelationGは一定である：

ポアソン点過程のEmptySpaceF関数およびNearestNeighborG関数は同一である：

両者はどちらもExponentialDistributionの累積分布関数に等しい：

一定強度関数を持つInhomogeneousPoissonPointProcessはPoissonPointProcessである：

円板上の点の数の分布：

同じ領域上の対応するポアソン点過程の点の数の分布：

より高次元で：

球の中の点の数の分布：

同じ領域上の対応するポアソン点過程の点の数の分布：

Wolfram Research (2020), PoissonPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

テキスト

Wolfram Research (2020), PoissonPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

CMS

Wolfram Language. 2020. "PoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

APA

Wolfram Language. (2020). PoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonPointProcess.html

BibTeX

@misc{reference.wolfram_2024_poissonpointprocess, author="Wolfram Research", title="{PoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonPointProcess.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_poissonpointprocess, organization={Wolfram Research}, title={PoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/PoissonPointProcess.html}, note=[Accessed: 21-November-2024 ]}