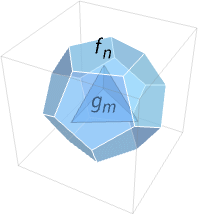
Polyhedron[{f1,…,fn}]
表示封闭曲面内的一个填充多面体,其多边形面为 fi.
Polyhedron[{f1,…,fn}{{g1,…,gm},…}]
表示有洞 {g1,…,gm},… 的多面体.
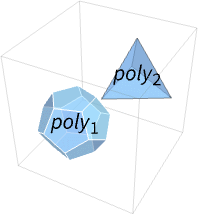
Polyhedron[{poly1,poly2,…}]
表示一组多面体 polyi.
Polyhedron[{p1,…,pn},data]
表示一个多面体,其中 data 中用整数 i 给出的坐标被认为是 pi.


Polyhedron
Polyhedron[{f1,…,fn}]
表示封闭曲面内的一个填充多面体,其多边形面为 fi.
Polyhedron[{f1,…,fn}{{g1,…,gm},…}]
表示有洞 {g1,…,gm},… 的多面体.
Polyhedron[{poly1,poly2,…}]
表示一组多面体 polyi.
Polyhedron[{p1,…,pn},data]
表示一个多面体,其中 data 中用整数 i 给出的坐标被认为是 pi.
更多信息和选项



- Polyhedron 可被用作几何区域及图形基元.
- Polyhedron[{f1,…,fn}] 是一个体积区域,表示具有多边形面 fi 的封闭曲面内的所有点.
- 如果来自任何方向上的点的直线穿过边界多边形面奇数次,则点是多面体的元素.
- Polyhedron[{f1,…,fn}{{g1,…,gm},…}] 指定一个有洞的多面体,其中,洞由外多面体 Polyhedron[{f1,…,fn}] 和一个或几个内多面体 Polyhedron[{g1,…,gm}],… 组成.
- 如果点 p 在外多面体中而不在任何内多面体中,则是多面体的元素.
- Polyhedron[{poly1,poly2,…}] 是一组有洞或没有洞的多面体 polyi,几何计算时将其视为 polyi 的并集.
- Polyhedron[{p1,…,pn},data] 实际上将 data 中作为坐标出现的整数 i 替换为相应的 pi.
-
Polyhedron[{p1,…,pn},{f1,…,fn}] 具有点 {po1,…,pok} 的多面体边界面 fi Polyhedron[{p1,…,pn},{{f1,…,fk}{{g1,…,gl},…}] 具有点 {po1,…,pok} 的外多面体边界面 fi,具有点 {pv1,…,pvl} 的内多面体边界面 gj 等. Polyhedron[{p1,…,pn},{{b1,…,bn},{f1,…,fk}{{g1,…,gl},…},…}] 几个多面体的集合 - 作为几何区域,多边形面 fi 可以具有任何嵌入维度,但必须都是简单多边形并具有相同的嵌入维度.
- 在图形中,多边形面 fi 的点可以是 Scaled 和 Dynamic 表达式.
- 图形渲染受 FaceForm、EdgeForm、Texture、Specularity、Opacity 和颜色等指令的影响.
- 可在图形中使用以下选项和设置:
-
VertexColors Automatic 要插值的顶点颜色 VertexNormals Automatic 用于着色的有效顶点法线 VertexTextureCoordinates None 用于纹理的坐标

范例
打开所有单元 关闭所有单元范围 (11)
图形 (8)
样式 (5)
Texture 可用于指定要在多面体的面上使用的纹理:
FaceForm 和 EdgeForm 可用于指定边和面的样式:
可用 VertexColors 指定顶点的颜色:
可用 VertexNormals 指定三维多边形在顶点处的法线:
坐标 (1)
使用 Scaled 坐标:
参见
PolyhedronCoordinates OuterPolyhedron InnerPolyhedron Cube Dodecahedron Icosahedron Octahedron Tetrahedron Cuboid Hexahedron Parallelepiped Prism Pyramid Simplex PolyhedronData CanonicalizePolyhedron RandomPolyhedron MeshRegion
Function Repository: PolyhedronCanonicalForm OutlinePolygons PolyhedronChop
文本
Wolfram Research (2019),Polyhedron,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Polyhedron.html.
CMS
Wolfram 语言. 2019. "Polyhedron." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Polyhedron.html.
APA
Wolfram 语言. (2019). Polyhedron. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Polyhedron.html 年
BibTeX
@misc{reference.wolfram_2025_polyhedron, author="Wolfram Research", title="{Polyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Polyhedron.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_polyhedron, organization={Wolfram Research}, title={Polyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Polyhedron.html}, note=[Accessed: 16-February-2026]}