x^y
![]() の
の ![]() 乗を与える.
乗を与える.




Power 
x^y
![]() の
の ![]() 乗を与える.
乗を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
 の形式の解に,可能な限り,厳密な有理数の結果が与えられる.
の形式の解に,可能な限り,厳密な有理数の結果が与えられる.- 複素数
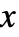 と
と 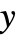 についてPowerは,
についてPowerは,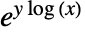 の主値を与える. »
の主値を与える. »  は,
は,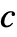 が整数の場合に限って自動的に
が整数の場合に限って自動的に 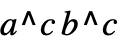 に変換される.
に変換される.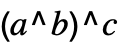 は,
は,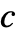 が整数の場合に限って自動的に
が整数の場合に限って自動的に 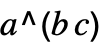 に変換される.
に変換される.- 特別な引数の場合,Powerは自動的に厳密値を計算する.
- Powerは任意の数値精度で評価できる.
- Powerは自動的にリストに縫い込まれる.
- Power[x,y]は,複素
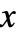 平面の
平面の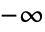 から0の範囲において非整数
から0の範囲において非整数 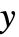 について不連続な分枝切断線を持つ.
について不連続な分枝切断線を持つ. - Power[x,y,z,…]はPower[x,Power[y,z,…]]と解釈される.
- PowerはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
予備知識
- Powerは,式を与えられた数で累乗する数学関数である.式Power[x,y]は通常短縮形のシンタックス x^y を使って表される,あるいは2Dタイプセット形式で xy として書かれる.ある数の1乗は,それ自体に等しく(
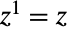 ),1の複素ベキは1に等しい(
),1の複素ベキは1に等しい(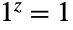 ).ベキ関数の逆関数は,Logで与えられるので,
).ベキ関数の逆関数は,Logで与えられるので,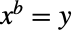 を
を 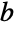 について解くと,
について解くと,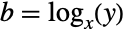 の主要解が返される.
の主要解が返される. - 式を2乗する操作は,「平方」として,式の3乗は「立方」として知られる.ベキを含む数量を組み合せる規則は,指数規則と呼ばれ,与えられたベキに底を累乗することは,累乗法として知られる.Power,Exp,Log,およびその関連関数を含む多くの式は,自動的に簡約されるか,SimplifyまたはFullSimplifyを使って簡約される.PowerExpandを使って形式的展開および関連の簡約化を行い,ExpToTrigを使ってPower式の三角法形式を得ることができる.
- 関数Sqrt[x]は,Power[x,1/2]を使って表される.自然対数の底Eを使った累乗法は,Exp[x]として入力されるが,Power[E,x]を使って表される.
- Power[x,y]は,非整数 y についての複素 x 平面で
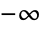 から0まで変化する y の分岐線法の非連続性を持つ.この分岐線法のため,Power[x,1/n]はデフォルトで負の実数 x と奇数の正の数 n について,実数根の代りに複素根を返す.実数値の n
から0まで変化する y の分岐線法の非連続性を持つ.この分岐線法のため,Power[x,1/n]はデフォルトで負の実数 x と奇数の正の数 n について,実数根の代りに複素根を返す.実数値の n 乗根を得るためには,Surd[x,n]を使う.特殊形CubeRoot[x]は,Surd[x,3]に対応する.
乗根を得るためには,Surd[x,n]を使う.特殊形CubeRoot[x]は,Surd[x,3]に対応する.
例題
すべて開く すべて閉じる例 (6)
スコープ (46)
数値評価 (9)
これは,![]() として定義されたPowerの一般定義に基づいている:
として定義されたPowerの一般定義に基づいている:
Surdを使って実根を得ることができる:
Powerは要素単位でリストと行列に縫い込まれる:
PowerはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる:
Aroundを使って平均的な場合の統計区間を計算する:
MatrixFunctionを使って行列のPower関数を計算することもできる:
特定の値 (4)
Power[x,3]=0.5であるような x の値を求める:
可視化 (5)
積分 (3)
級数展開 (4)
Seriesを使ってテイラー(Taylor)展開を求める:
SeriesCoefficientを使った級数展開の一般項:
関数の恒等式と簡約 (6)
アプリケーション (5)
特性と関係 (27)
Power[x,1/n]または![]() を使って主複素根を求める:
を使って主複素根を求める:
Surd[x,n]を使って n 番目の実根を求める:
PowerExpandを使って形式的に簡約する:
ExpToTrigを使って三角法の形を求める:
Expandを使って多項式のベキに展開する:
Powerは多くの数学関数の特殊形に現れる:
PowerはDifferenceRootとして表すことができる:
Powerの級数展開における一般項:
Powerの母関数:
FindSequenceFunctionはPower数列を認識する:
Powerの指数母関数:
GeneralizedPowerを使って任意の二項演算の整数乗を表す:
考えられる問題 (13)
Powerは常に主根を計算する:
Chopを使って小さい虚部を削除する:
機械精度の場合,分枝切断線上で不正確な数値結果が与えることがある:
ベキの中にはどのようなコンピュータにとっても大きすぎるものもある:
1の記号ベキは1が厳密数あるいは機械精度数である場合にのみ評価される:
Powerは行列に対して要素単位で適用される:
行列のベキにはMatrixPowerを使う:
テクニカルノート
-
▪
- 数の四則演算
関連するガイド
-
▪
- 算術関数 ▪
- 行列の操作 ▪
- 行列と線形代数 ▪
- ベクトル操作 ▪
- 初等関数 ▪
- 画像の処理と解析 ▪
- Wolfram言語のシンタックス ▪
- 数学関数 ▪
- GPU計算 ▪
- 音声編集 ▪
- NVIDIAを使ったGPU計算 ▪
- Appleを使ったGPU計算
履歴
1988 で導入 (1.0) | 2021 で更新 (13.0)
テキスト
Wolfram Research (1988), Power, Wolfram言語関数, https://reference.wolfram.com/language/ref/Power.html (2021年に更新).
CMS
Wolfram Language. 1988. "Power." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Power.html.
APA
Wolfram Language. (1988). Power. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Power.html
BibTeX
@misc{reference.wolfram_2025_power, author="Wolfram Research", title="{Power}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Power.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_power, organization={Wolfram Research}, title={Power}, year={2021}, url={https://reference.wolfram.com/language/ref/Power.html}, note=[Accessed: 18-February-2026]}