QuantityDistribution[dist,unit]
表示一个数量分布 dist,单位由 unit 指定.
QuantityDistribution[dist,{unit1,unit2,…}]
表示单位为 {unit1,unit2,…} 的多变量分布.


QuantityDistribution
QuantityDistribution[dist,unit]
表示一个数量分布 dist,单位由 unit 指定.
QuantityDistribution[dist,{unit1,unit2,…}]
表示单位为 {unit1,unit2,…} 的多变量分布.
更多信息

- QuantityDistribution 常常通过在参数中使用数量而产生,从含有数量的数据中导出或估计.
- QuantityDistribution 会自动试着将未知单位字符串解析成标准形式的单位. »
- QuantityDistribution[dist,unit] 等价于 TransformedDistribution[Quantity[x,unit],x dist]. »
- 分布函数的参数的单位被假设与 unit 兼容. »
- 单变量分布的分布函数的值有下述单位:
-
CDF 没有单位 InverseCDF unit SurvivalFunction 没有单位 InverseSurvivalFunction unit - PDF 的值和 HazardFunction 的的单位为: »
-
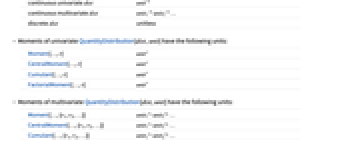
连续单变量 dist unit-1 连续多变量 dist unit1-1 unit2-1 … 离散 dist 没有单位 - 单变量 QuantityDistribution[dist,unit] 的矩的单位为:
-
Moment[…,r] unit r CentralMoment[…,r] unit r Cumulant[…,r] unit r FactorialMoment[…,r] unit r - 多变量 QuantityDistribution[dist,unit] 的矩的单位为:
-
Moment[…,{r1,r2,…}] unit1r1 unit2r2 … CentralMoment[…,{r1,r2,…}] unit1r1 unit2r2 … Cumulant[…,{r1,r2,…}] unit1r1 unit2r2 … FactorialMoment[…,{r1,r2,…}] unit1r1 unit2r2 … - 矩母函数要求参数为带有单位的数量,其单位应为 QuantityDistribution 的单位的倒数.
- 从 QuantityDistribution 得到的样本为 Quantity 或 QuantityArray.
- QuantityDistribution 可与 Mean、CDF、RandomVariate、QuantityMagnitude 或 Expectation 这样的函数一起使用.
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (29)
基本用途 (11)
求一个设备的平均服务时间,其寿命符合 WeibullDistribution-模型:
CDF 的参数被认为是时间量:
计算 QuantityDistribution 的分位数:
从 QuantityDistribution 得到的样本为 Quantity 或 QuantityArray:
带有数量的连续分布的 PDF:
带有数量的离散分布的 PDF 是没有单位的:
带有数量的连续分布的 HazardFunction 的单位是分布的单位的倒数:
数量分布的 QuantityMagnitude 和 QuantityUnit:
用 UnitConvert 将分布的单位转换至兼容单位:
用 UnitSimplify 将单位简化为 "Volts":
构建 (6)
在 QuantityDistribution 中,可以用数量来指定单位:
用 TransformedDistribution 来定义随机数量的分布:
估计 (4)
EstimatedDistribution 给出带有拟合参数的 QuantityDistribution:
可能的情况下,FindDistributionParameters 给出带有 Quantity 值的规则:
将这些参数代入 QuantityDistribution 中的模型:
QuantityDistribution[dist,units] 中幅值 dist 的参数是数字:
导出分布 (8)
截尾后的 QuantityDistribution 为另一个 QuantityDistribution:
删失后的 QuantityDistribution 为另一个 QuantityDistribution:
互相兼容的 QuantityDistribution 的混合为另一个 QuantityDistribution:
将几个 QuantityDistribution 拼接在一起所得的分布为另一个 QuantityDistribution:
数量分布的 ProductDistribution:
乘积分布还是 QuantityDistribution:
QuantityDistribution 的参数混合分布还是 QuantityDistribution:
顺序统计量的分布是 QuantityDistribution:
QuantityDistribution 的 QuantityDistribution:
结果和 Quantity 的组合的性质一致:
应用 (8)
一辆从伊利诺伊州的香槟市开往芝加哥市的的汽车的平均速度可以被描述为一个三角形分布的随机变量:
绘制立方体体积的 PDF:
用 NormalDistribution 拟合数据:
比较直方图与估计的 PDF:
据信一个饭馆中顾客的等候时间服从指数分布,平均等候时间为5分钟:
一个元件的寿命为 WeibullDistribution,其形状参数为2,尺度参数为997.5小时. 求元件寿命超过300小时的概率:
求500小时后元件依然正常工作的概率,假设它已经正常工作超过了300个小时:
将分布拟合至 PERTDistribution:
气体分子沿任意方向的速度密度函数服从正态分布,其均值为0,标准偏差为 ![]() . 氢分子在 573K 的温度下的标准偏差为:
. 氢分子在 573K 的温度下的标准偏差为:
通过测量一个摆的周期 ![]() 和长度
和长度 ![]() ,利用
,利用 ![]() 即可得出重力加速度. 可用 BatesDistribution 来模拟五次重复测量周期中的不确定性:
即可得出重力加速度. 可用 BatesDistribution 来模拟五次重复测量周期中的不确定性:
用分辨率为 1 毫米的尺子来测量摆的长度,可用 UniformDistribution 来模拟不确定性:
属性和关系 (6)
带有无量纲单位的 QuantityDistribution 会自动转成幅值分布:
用 QuantityMagnitude 和 QuantityUnit 提取分布和单位:
QuantityDistribution[dist,unit] 等价于 TransformedDistribution:
QuantityDistribution 的偏度和峰度是没有单位的:
在分布域上对有单位的连续分布的 PDF 进行积分,结果为1:
可能存在的问题 (4)
文本
Wolfram Research (2016),QuantityDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/QuantityDistribution.html.
CMS
Wolfram 语言. 2016. "QuantityDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/QuantityDistribution.html.
APA
Wolfram 语言. (2016). QuantityDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/QuantityDistribution.html 年
BibTeX
@misc{reference.wolfram_2025_quantitydistribution, author="Wolfram Research", title="{QuantityDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/QuantityDistribution.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_quantitydistribution, organization={Wolfram Research}, title={QuantityDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/QuantityDistribution.html}, note=[Accessed: 05-February-2026]}