RSolve

RSolve[eqn,a[n],n]

a[n]についての再帰方程式を解く．

RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

再帰方程式系を解く．

RSolve[eqn,a[n1,n2,…],{n1,n2,…}]

偏再帰方程式を解く．

詳細とオプション

  • RSolve[eqn,a,n]は a の解を純関数として与える．
  • この方程式は a[n+λ]の形式でオブジェクトを含むことができる．ただし，λ は定数あるいは a[ψ[n]], a[ψ[ψ[n]], a[ψ[…[ψ[n]]…]]の形式の一般的なオブジェクトである．ψ は次のような形式を取ることができる．
  • n+λ算術差分方程式
    μ n幾何方程式または 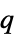差分方程式
    μ n+λ算術幾何関数差分方程式
    μ nα幾何ベキ関数差分方程式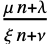
    線形分数関数差分方程式
  • 端末条件の指定のために，a[0]==val のような方程式を与えることができる．
  • RSolveは，十分な端末条件が指定されていない場合は，未定定数を導入する一般的な解を返す．
  • a∈Vectors[m]あるいは a∈Matrices[{m,p}]という指定を使って従属変数 a がベクトル値あるいは行列値の変数であることを示すことができる． » »
  • RSolveが導入する定数には連続する整数で指標が付けられる．オプションGeneratedParametersで各指標に適用する関数を指定する．デフォルトはGeneratedParameters->Cであり，これによって定数C[1], C[2], … が与えられる．
  • GeneratedParameters->(Module[{C},C]&)は，たとえRSolveが別の機会に呼び出されても積分定数が一意的であることを保障する．
  • 偏再帰方程式の場合，RSolveは任意の関数C[n][…]を生成する．
  • RSolveが与える解はSumが明示的に実行できない総和を含むことがある．そのような総和には局所的な名前を持ったダミー変数が使われる．
  • RSolveはSolveによる陰的な解を与えることがある．
  • RSolveは常差分方程式と 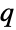差分方程式の両方を解くことができる．
  • RSolveは常差分方程式だけでなく差分代数方程式も扱うことができる．
  • RSolveは定数係数を持つ任意の階数の線形再帰方程式を解くことができる．また，多くの非線形方程式に加え非定数係数を持つ二階までの線形方程式も解くことができる．

例題

すべて開くすべて閉じる

例  (4)

差分方程式を解く：

境界条件を入れる：

a についての「純関数」解を得る：

解を式に代入する：

関数方程式を解く：

スコープ  (40)

基本的な用法  (7)

一階差分方程式の一般解を計算する：

初期条件を加えることで，特殊解を得る：

一階差分方程式の解をプロットする：

値の表を作る：

第2引数に a を使うことで，差分方程式の解を確かめる：

より高階の差分方程式の一般解を得る：

特殊解を得る：

差分方程式系を解く：

解をプロットする：

解を確かめる：

偏差分方程式を解く：

特殊解を得る：

結果の解をプロットする：

一般解中で，任意の定数に異なる名前を使う：

線形差分方程式  (7)

幾何学方程式：

変数係数を持つ一階の方程式：

三階定数係数方程式：

初期値条件：

解をプロットする：

二階非同次方程式：

初等関数による二階変数係数方程式：

オイラー・コーシー(Euler-Cauchy)方程式：

一般に，特殊関数は解を表すように求められる：

定数係数を持つより高次の非同次方程式：

非線形差分方程式  (5)

解くことができるロジスティック方程式：

リッカティ(Riccati)方程式：

三角関数と双曲線関数による解：

高階の方程式：

非線形たたみ込み方程式：

差分方程式系  (8)

定数係数を持つ線形系：

境界条件付き：

解をプロットする：

線形分数系：

対角系：

多項式解を持つ変数係数線形系：

線形定数係数差分代数系：

指数2の系：

ベクトル変数を使って線形系を解く：

行列変数を使って線形系を解く：

定数係数を持つ常微分方程式の非同次線形系を解く：

偏差分方程式  (3)

定数係数を持つ一階線形偏差分方程式：

関数Sin[2k]を自由関数C[1]の代りに使う：

結果の解をプロットする：

階数が二，三，四の定数係数線形方程式：

非同次方程式：

変数係数線形方程式：

q差分方程式  (6)

一階定数係数 差分方程式：

同じ方程式を表す方法：

初期値：

二階方程式：

三階方程式：

非同次方程式：

に数値を使う：

解をプロットする：

線形変化係数方程式：

非線形方程式：

リッカティ方程式：

差分方程式の線形定数係数系：

関数差分方程式  (4)

算術差分方程式の一般解を求める：

解を確かめる：

算術幾何差分方程式について初期値問題を解く：

解をプロットする：

線形分数差分方程式を解く：

解の値の表を作る：

幾何ベキ差分方程式を解く：

解を確かめる：

一般化と拡張  (1)

境界条件なしで2つの生成されたパラメータを与える：

1つの境界条件：

2つの境界条件：

オプション  (1)

GeneratedParameters  (1)

異なる名前の定数を使う：

下付き文字を含む定数を使う：

アプリケーション  (11)

これは，利子 r が元本 p のみに対して払われたときに，年 n における金額 a[n]のモデルを出す：

以下では現在額 a[n]に対して利子が払われる，すなわち複利である：

ここでは，a[n]は n 枚の円板についての「ハノイの塔」問題で必要な移動回数を表している：

ここでは，a[n]は n×3の空間を2×1のタイルで埋めるのに何通りあるかを表している：

二分検索問題の比較回数：

高速フーリエ変換の代数操作の数：

積分 は差分方程式を満足する：

積分 は差分方程式を満足する：

の級数係数の差分方程式：

対角要素 を持つ n×n 三重対角行列の行列式は満足する：

これは，次元 n の単位球の表面積 s[n]のモデルである：

次元 n の単位球体の体積：

にニュートン法を適用する，すなわちを計算する：

オイラーの前進法をに適用すると以下が得られる：

Karatsuba乗算の複雑さを説明する差分方程式を解く：

学校教科書の乗算の複雑さと比較する：

特性と関係  (9)

解はその差分方程式と境界方程式を満足する：

Sumに対応する差分方程式：

Productに対応する差分方程式：

RSolveは，解についての規則を返す：

RSolveValueは，解についての式を返す：

RSolveは差分方程式の記号解を求める：

RecurrenceTableは，同じ問題についての手続き的解を生成する：

FindLinearRecurrenceは，リストについての最小線形再帰を求める：

RSolveは，再帰を満足する数列を求める：

RecurrenceFilterを使って信号にフィルタをかける：

RSolveを使って対応する差分方程式を解く：

ARProcessに基づいて時系列の次の値を予測する：

RSolveを使って同じ結果を得る：

RFixedPointsを使って2つの再帰方程式の系の固定点を求める：

RStabilityConditionsを使って固定点の安定性を解析する：

固定点を初期条件として使って系を解く：

与えられた初期条件について系を解く：

解をプロットする：

考えられる問題  (5)

結果は記号的な総和と積を含むことがある：

大文字の と を独立変数として使うことはできない：

小文字の または に置き換えると問題は解決する：

この差分方程式の解は文字列として一意的である：

関数として，これは周期1の関数としてまでしか一意的ではない：

境界値問題には複数の解があることがある：

方程式が下付き文字がある変数を含む場合の解を確かめる：

おもしろい例題  (1)

関数の n 次の反復または合成を計算する：

Wolfram Research (2003), RSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/RSolve.html （2023年に更新）.

テキスト

Wolfram Research (2003), RSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/RSolve.html （2023年に更新）.

CMS

Wolfram Language. 2003. "RSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/RSolve.html.

APA

Wolfram Language. (2003). RSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RSolve.html

BibTeX

@misc{reference.wolfram_2024_rsolve, author="Wolfram Research", title="{RSolve}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RSolve.html}", note=[Accessed: 13-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rsolve, organization={Wolfram Research}, title={RSolve}, year={2023}, url={https://reference.wolfram.com/language/ref/RSolve.html}, note=[Accessed: 13-November-2024 ]}