Root

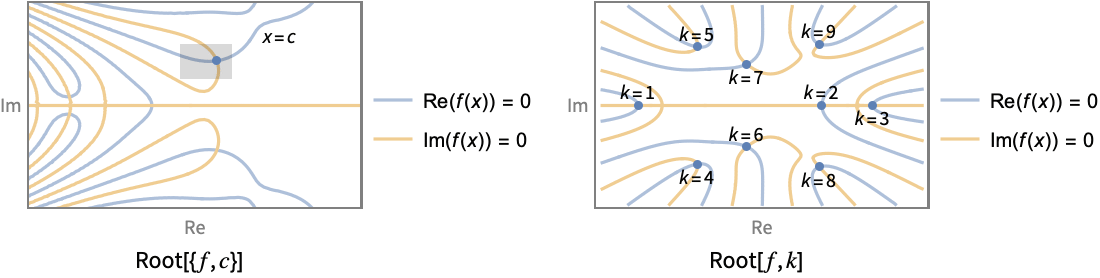
Root[{f,c}]

x=c 近傍における一般方程式 f[x]0の厳密解を表す．

Root[{{f1,…,fn},{c1,…,cn}},j]

{x1,…,xn}={c1,…,cn}近傍の方程式系{f1[x1,…,xn]0,…,fn[x1,…,xn]0}の厳密根の j 番目の座標を表す．

Root[f,k]

正方程式 f[x]0の厳密に k 次の根を表す．

Root[{f1,f2,…},{k1,k2,…}]

aiが 整方程式 fi[a1,…,ai-1,x]0の第 ki根となるような，厳密ベクトル{a1,a2,…}の最後の座標を表す．

詳細とオプション

  • Rootは，f が整数係数を持つ多項式の場合は代数的数として，そのような多項式 f が存在しない場合は超越数としても知られている．
  • Rootはしばしば厳密数を表すために使われ，代数，微積分，最適化，幾何学のさまざまな関数によって自動的に生成される．
  • Rootは厳密数を方程式 f[x]0の解として表す．追加的な情報でどの根を意図しているのかが指定できる．
  • Root数は，他の任意の数と同じように，厳密計算と近似計算の両方で使うことができる．
  • Root数はとしてフォーマットされる．ただし，approx は数値近似である．精度 p の近似はN[,p]を使って計算できる．
  • ほとんどの用法で，Rootオブジェクトは自動的に生成され，直接使うことができる．上級ユーザは，コードが直接Rootオブジェクトを生成するようなときは別の表現法についてのより深い理解を持つ必要である．
  • 方程式のどの根を表すのかを指定するために使用される，近傍表現Root[{f,c}]とインデックス表現Root[f,k]の2つのメカニズムがある．
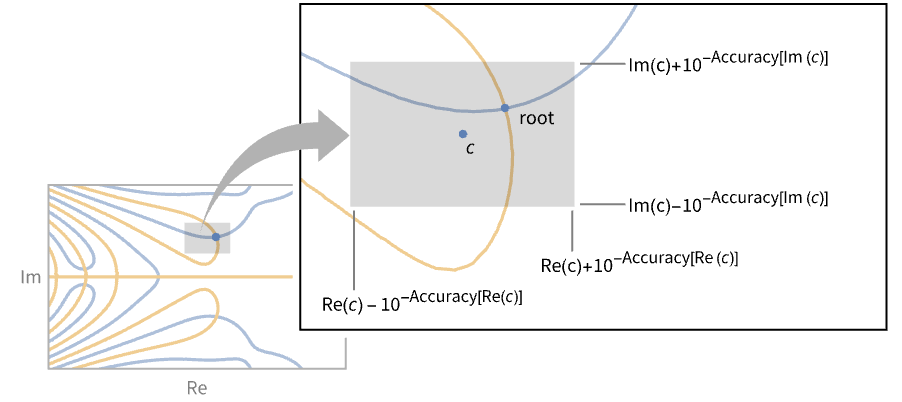
  • 根近傍表現Root[{f,c}]は，c を中心として幅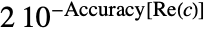がで高さが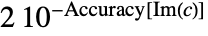の近傍長方形だけでなく方程式 f[x]0も指定する．
  • 系Root[{{f1,…,fn},{c1,…,cn}},j]の根近傍表現も同様に方程式系{f1[x1,…,xn]0,…,fn[x1,…,xn]0}と異なる座標の ciからの長方形の積によって与えられる近傍を与える．
  • 根近傍表現Root[{f,c,m}]は c で与えられる近傍で f[x]0が多重度 m の根を持つように指定する．しかし，与えられるのは狭い間隔の根のクラスタかもしれない．近傍 c を細分化する，つまり根の近似の精度をより高くすることで分離できるかもしれない． »
  • 根インデックス表現Root[f,k]は多項式関数 f のみを適用する．根のインデックス付けは，まず次数の昇順で実根を取る．有理係数を持つ多項式については，根の複素共役ペアが連続するインデックスを持つ．
  • 系Root[{f1,f2,…,fk},{k1,k2,…,kn}]の根インデックス表現は，整方程式の三角形にのみ適用される．方程式 f1[x1]0, f2[x1,x2]0, …, fn[x1,x2,…,xn]0が与えられると，r1を f1[x1]0の k1次根として，r2を f2[r1,x2]0の k2次根としてというように再帰的に定義し，最後に rnをfn[r1,…,rn-1,xn]0の kn次根として定義する．表現された根は rnである．

例題

すべて開くすべて閉じる

例  (4)

五次方程式の解：

数値による値：

指数対数方程式の実数解：

方程式系の実数解：

超越方程式系の解の例：

スコープ  (22)

基本的な用法  (5)

厳密値の中には自動的に生成されるものもある：

高精度で評価する：

厳密な比較：

累乗根をRootオブジェクトに変換する：

Rootオブジェクトを累乗根に変換する：

Rootの省略されたフォーマットを無効にする：

省略されたフォーマットを再度有効にする：

一変量関数の根  (4)

指数対数関数の実根：

Root表現には一変量関数と根を分離する近似が含まれる：

Rootオブジェクトは厳密な数式である：

境界領域の解析関数の根：

三重根：

この表現は次数が$MaxRootDegreeを超える多項式の根に使われる：

根の表現に使われた近似はに等しいが，根はそうではない：

多変量の系の根  (1)

超越方程式系の解の例を求める：

根は厳密な数式である：

Root表現は多変量の系と根を分離する近似を含む：

一変量多項式の根  (10)

有理係数を持つ一変量多項式の根は代数的数である：

多項式は自動的に簡約される：

最小多項式は常に既約で原始的である：

MinimalPolynomialを使って最小多項式を抽出する：

代数的数を表すRootオブジェクトには3つの引数がある：

第3引数は（デフォルト値の）0か1で，使用する根の分離法を示す：

使用する根の分離法が非実数根の順序に影響するかもしれない：

次数が1または2の多項式の根は自動的に簡約される：

代数的数を代数的に組み合せたものは代数的数である：

RootReduceを使って結果を単一のRootオブジェクトとして表す：

最小多項式は急速に成長する可能性があるので，正規化は自動的には行われない：

代数的数の複素成分：

厳密な数値係数を持つ多項式のRootは厳密な数値オブジェクトである：

記号パラメータを含む係数を持つ多項式の根：

実数値根をプロットする：

パラメータについての級数を求める：

分岐点における根のPuiseux級数を求める：

記号係数を持つ二次方程式の根：

a, b, c および根が実数のとき，根は常にその値で並べられる：

二次方程式の根についての「標準」的な公式は根の順序を保証しない：

三角多項式系の根  (2)

方程式の三角系の実根：

Root表現は三角多項式系と根のインデックスを含む：

Rootオブジェクトは厳密な数式である：

有理係数を持つ多項式系の根は代数的数の座標を持つ：

最小多項式の次数は，一般に，多項式系の次数の積である：

この表現は代数的数の係数を持つ多項式の根に用いられる：

根を正規の代数的数の表現に変換する：

オプション  (1)

ExactRootIsolation  (1)

Root[f,k]は，デフォルトで，検証済みの数値手法を使って多項式の複素根を分離する．ExactRootIsolationTrueと設定するとRootが記号手法を使うようになるが，これは大抵の場合非常に遅い．

ExactRootIsolationの設定値はRootオブジェクトの第3引数に反映される：

根の分離は最初に根の数値が必要になったときに行われる：

記号的な複素根分離メソッドは有効な数値によるものより一般に時間がかかる：

根分離メソッドは非実根の順番に影響を与えることがある：

アプリケーション  (19)

閉じた形の任意次数の整方程式をRootに関して解く：

ヒルベルト(Hilbert)行列の特性方程式を解く：

Eigenvaluesを使う：

パラメータ化された多項式の最小値を求める：

任意の次数の定係数微分方程式を解く：

任意の次数の定係数微分方程式を解く：

方程式の三角系の解を求める：

Root[f,k]の形式で解を表す：

ここでは，Root[f,k]表現が次数1000000の多項式を含む可能性がある：

解の近似値を計算する：

区分関数を解く：

一変量の指数対数方程式と不等式を実数上で解く：

一変量初等関数方程式を境界区間と領域上で解く：

一変量解析方程式を境界区間と領域上で解く：

高次数の疎な多項式と代数関数の実根を求める：

一変量超越最適化問題を解く：

指数対数の不等式条件を持つ区分関数を積分する：

固い六角形のエントロピー定数を評価する：

ケプラー(Kepler)の方程式を解く：

ラプラス(Laplace)の極限定数を計算する：

根をパラメータの関数としてプロットする：

凸最適化問題を解く：

超越方程式系と不等式系の解の例：

特性と関係  (11)

Rootオブジェクトは厳密値を表す：

任意精度の近似を計算する：

MinimalPolynomialを使って代数的数の最小多項式を求める：

ToRadicalsを使ってRootオブジェクトを累乗根の算術の組合せに変換しようとする：

次数が4を超えない多項式の根はすべて累乗根で表現できる：

RootReduceを使って演算を含めて代数的数を正規化する：

三角系から：

AlgebraicNumberを有理数の固定した単純な拡張内の計算に使う：

AlgebraicNumberオブジェクトに対する有理操作はAlgebraicNumberオブジェクトを生成する：

ToNumberFieldを使って与えられた代数的数を同じ単純な拡張の要素として表現する：

共通の単純な拡張あるいは有理数内で計算する：

RootSumは多項式の根の上で関数の値の総和を表す：

Normalを使って明示的な根で総和を表す：

有理関数については，総和は根を求めずに計算できる：

Rootオブジェクトの組合せを簡約する：

Rootオブジェクト内のパラメータについての方程式を解く：

ImplicitDを使って方程式の陰解の導関数を計算する：

の導関数を直接計算して得られた結果と比較する：

方程式の陰的な解の級数展開を計算する：

AsymptoticSolveを使ってすべての根の級数展開を求める：

RootApproximantを使って与えられた数を近似するRootオブジェクトを生成する：

考えられる問題  (5)

分岐点における級数は全方向に有効ではないことがある：

標準化はパラメータを持たない根についてのみ可能である：

パラメータ化された根は複素パラメータ平面上で複雑な分枝切断線を持つ可能性がある：

非多項式のRootオブジェクトは異なる根のクラスタを表すことがある：

より高い精度で数値計算すると根の1つが近似される：

続く計算でも根の選択は同じである：

非整数係数を持つ根については，$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

おもしろい例題  (1)

ピソット(Pisot)数の高次ベキはほぼ整数に等しい：

Wolfram Research (1996), Root, Wolfram言語関数， https://reference.wolfram.com/language/ref/Root.html （2021年に更新）.

テキスト

Wolfram Research (1996), Root, Wolfram言語関数， https://reference.wolfram.com/language/ref/Root.html （2021年に更新）.

CMS

Wolfram Language. 1996. "Root." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Root.html.

APA

Wolfram Language. (1996). Root. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Root.html

BibTeX

@misc{reference.wolfram_2024_root, author="Wolfram Research", title="{Root}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Root.html}", note=[Accessed: 04-May-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_root, organization={Wolfram Research}, title={Root}, year={2021}, url={https://reference.wolfram.com/language/ref/Root.html}, note=[Accessed: 04-May-2024 ]}