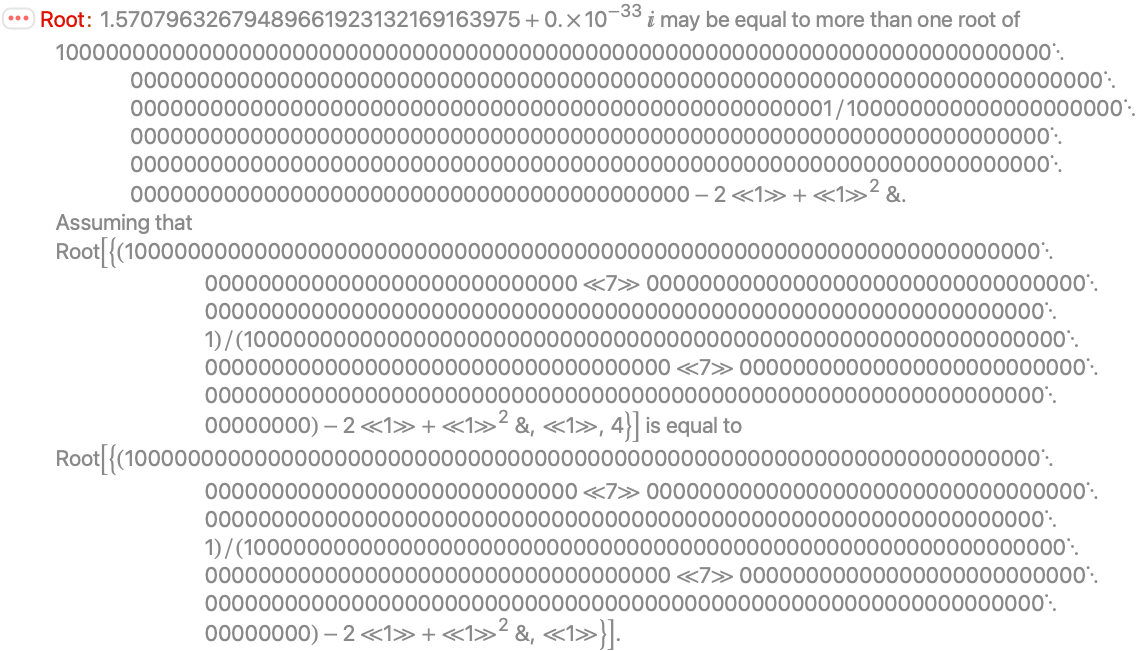Root

Root[{f,c}]

表示一般方程 f[x]0 在 x=c 附近的精确根.

Root[{{f1,…,fn},{c1,…,cn}},j]

表示方程组 {f1[x1,…,xn]0,…,fn[x1,…,xn]0} 在 {x1,…,xn}={c1,…,cn} 附近的精确根的第 j 个坐标.

Root[f,k]

表示多项式方程 f[x]0 的 k 次方根.

Root[{f1,f2,…},{k1,k2,…}]

表示精确向量 {a1,a2,…} 的最后一个坐标，使得 ai 是多项式方程 fi[a1,…,ai-1,x]0 的 ki 次方根.

更多信息和选项

  • 当 f 是系数为整数的多项式时，Root 也称为代数数，当这样的多项式不存在时，称为超越数.
  • Root 通常用于表示一个精确的数字，由各种代数、微积分、优化和几何函数自动生成.
  • Root 表示一个精确数，作为方程 f[x]0 的解，附加信息指定了哪个根是预期的.
  • Root 数可以像任何其他数值一样用于精确和近似计算.
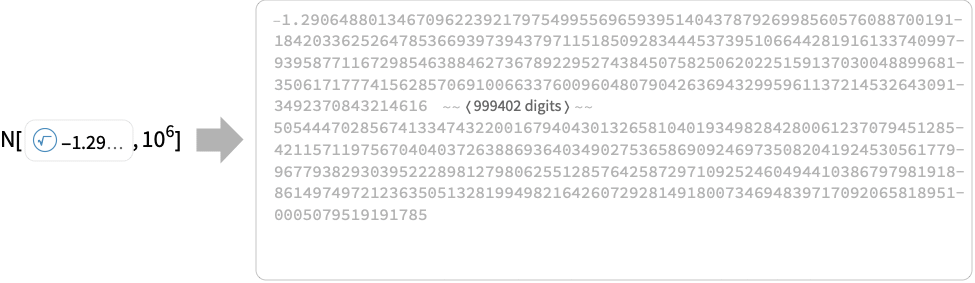
  • Root 数的格式为 ，其中 approx 是一个数值近似. 精度为 p 的近似可以使用 N[,p] 计算.
  • 对于大多数用途，Root 对象是自动生成的，可以直接使用. 对于高级用途，当您的代码要直接生成 Root 对象时，需要对不同的表示形式有更深入地了解.
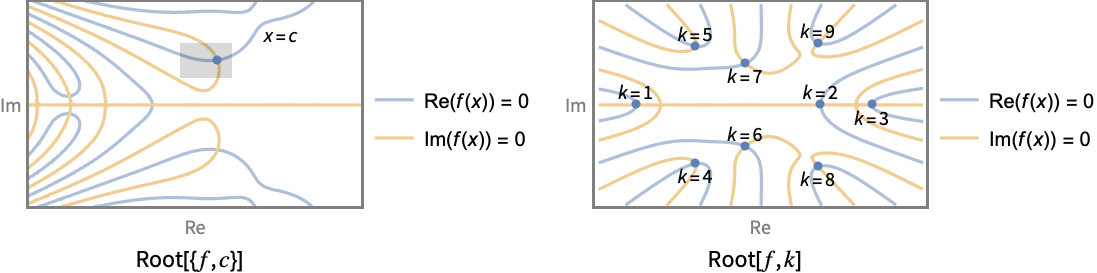
  • 有两种不同的机制用于指定表示方程的哪个根，邻域表示 Root[{f,c}] 和索引表示 Root[f,k].
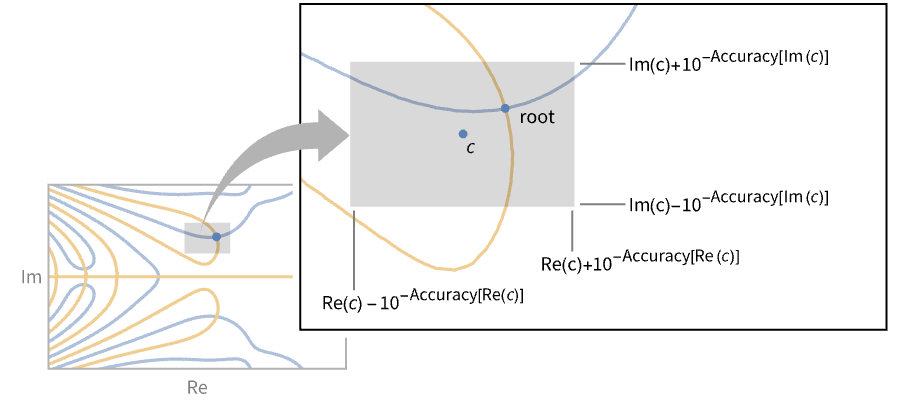
  • 根邻域表示 Root[{f,c}] 指定方程 f[x]0，以及以 c 为中心，宽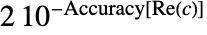度为 ，高度为 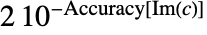的邻域矩形.
  • 系统 Root[{{f1,…,fn},{c1,…,cn}},j] 的根邻域表示类似地指定一个方程组 {f1[x1,…,xn]0,…,fn[x1,…,xn]0} 和由来自 ci 的不同坐标的矩形乘积给出的邻域.
  • 根邻域表示 Root[{f,c,m}] 指定 f[x]0 在由 c 给定的邻域中具有重数为 m 的根. 但这可能是一组间隔紧密的根，通过细化邻域 c，即更高精度的根近似，可能会将它们分开. »
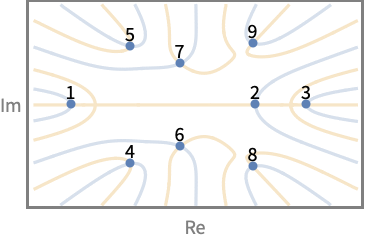
  • 根索引表示 Root[f,k] 仅适用于多项式函数 f. 根的索引首先取实根，按升序排列. 对于具有有理系数的多项式，根的复共轭对具有连续的索引.
  • 系统 Root[{f1,f2,…,fk},{k1,k2,…,kn}] 的根索引表示仅适用于多项式方程的三角系统. 已知方程f1[x1]0，f2[x1,x2]0，…，fn[x1,x2,…,xn]0，我们递归地定义 r1 为 f1[x1]0 的 k1 次方根，r2 为 f2[r1,x2]0 的 k2 次方根，……，rn 为 fn[r1,…,rn-1,xn]0 的 kn 次方根. 表示的根是 rn.

范例

打开所有单元关闭所有单元

基本范例  (4)

五次方程的解：

数值：

指数-对数方程的实数解：

方程组的实解：

超越方程组的解的实例：

范围  (22)

基本用法  (5)

自动生成某些精确值：

高精度求解：

精确比较：

将根式转换为 Root 对象：

将 Root 对象转换为根式：

禁用 Root 的省略格式：

重新启用省略格式：

单变量函数的根  (4)

指对数函数的实根：

Root 表示涉及一个单变量函数和一个隔离根的近似值：

Root 对象是精确的数值表达式：

有界区域内解析函数的根：

三重根：

此表示用于次数超过 $MaxRootDegree 的多项式的根：

用于表示根的近似值等于 ，但根不是：

多变量系统的根  (1)

求超越方程组的解的实例：

根是精确的数值表达式：

Root 表示涉及一个多变量系统和一个隔离根的近似：

单变量多项式的根  (10)

具有有理系数的单变量多项式的根是代数数：

多项式自动约化：

最小多项式总是不可约化且初等的：

使用 MinimalPolynomial 提取最小多项式：

代表代数数的 Root 对象具有三个参数：

代表代数数的根对象具有三个参数：

所用的根隔离方法可能会影响非实根的排序：

1 次和 2 次多项式的根自动化简：

代数数的代数组合是代数数：

使用 RootReduce 将结果表示为单个 Root 对象：

规范化不是自动完成的，因为最小多项式可以快速增长：

代数数的复数部分：

具有精确数值系数的多项式的 Root 是一个精确数值对象：

系数涉及符号参数的多项式的根：

绘制实值根：

求关于参数的级数：

在分支点处求根的 Puiseux 级数：

具有符号系数的二次方的根：

当 a、b、c 和根为实数时，根始终按其值排序：

二次方根的“标准”公式不保证根的顺序：

三角多项式系统的根  (2)

三角方程组的实根：

Root 表示涉及三角多项式系统和根索引：

Root 对象是一个精确的数值表达式：

具有有理系数的多项式系统的根具有代数数坐标：

最小多项式的次数通常是系统多项式的次数的乘积：

此表示用于具有代数数系数的多项式的根：

将根转换为规范的代数数表示：

选项  (1)

ExactRootIsolation  (1)

Root[f,k] 默认使用经过验证的数值方法隔离多项式的复根. 设置 ExactRootIsolationTrue 将使 Root 采用通常慢得多的符号方法.

ExactRootIsolation 的设置受到 Root 对象的第 3 个自变量的影响：

根的首次分离需要数值根：

符号的复数根的分离方法通常较有效一个数值根要慢：

根的分离方法可能会影响非实数根的次序：

应用  (19)

按照 Root 的封闭形式求解任意次数的多项式方程：

求解一个 Hilbert 矩阵的特征方程：

用 Eigenvalues：

求出参数多项式的最小值：

求出任意次数的常系数微分方程：

求解任意次数的常系数微分方程：

求三角方程组的解：

以 Root[f,k] 格式表示解：

这里，Root[f,k] 表示法应该包含次数为 1000000 的多项式：

计算解的近似值：

求解一个分段函数：

求解单个指数-对数方程和不等式的实数解：

求解有限区域的初等函数方程：

求解有限区域的解析函数方程：

求解高阶稀疏多项式和代数函数的实根：

求解单超越优化问题：

带有指数-对数不等条件的分段函数积分：

计算六边形熵常数：

求解 Kepler 方程：

计算拉普拉斯限制常数：

绘制作为参数函数的一个根：

求解凸优化问题：

求超越方程和不等式系统的解的实例：

属性和关系  (11)

Root 对象代表精确的数：

计算任意精度的近似值：

使用 MinimalPolynomial 求代数数的最小多项式：

使用 ToRadicals 尝试将 Root 对象转换为根式的算术组合：

次数不超过 4 的多项式的所有根都可以用根式表示：

用 RootReduce 规范化代数，包括来自操作：

从一个三角形系统：

在有理数的固定简单扩展中使用 AlgebraicNumber 进行计算：

对 AlgebraicNumber 对象的有理运算生成 AlgebraicNumber 对象：

使用 ToNumberField 把给定的代数数表示为相同简单扩展的元素：

在常见的简单扩展或有理数中执行计算：

RootSum 表示多项式根上函数值的总和：

使用 Normal 使用显式根表示总和：

对于有理函数，可以在不求根的情况下计算和：

化简包含 Root 对象的组合：

求解 Root 对象中参数的方程：

用 ImplicitD 计算方程隐式解的导数：

与直接计算 的导数得到的结果比较：

计算方程隐式解的级数展开式：

使用 AsymptoticSolve 求所有根的级数展开式：

使用 RootApproximant 生成近似给定数值的 Root 对象：

可能存在的问题  (5)

在分支点的级数在所有方向上可能不一定有效：

规范化仅对无参数根有效：

参数根在复平面上有复杂的分支线：

一个非多项式 Root 对象可以代表一组不同的根：

带有较高精度的数值计算产生一个近似根：

对于后续计算，根的选择保持不变：

对于具有非整数系数的根，可能需要 $MaxExtraPrecision 的较大设置：

巧妙范例  (1)

Pisot 数的一个较高幂是一个近似整数：

Wolfram Research (1996)，Root，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Root.html （更新于 2021 年）.

文本

Wolfram Research (1996)，Root，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Root.html （更新于 2021 年）.

CMS

Wolfram 语言. 1996. "Root." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/Root.html.

APA

Wolfram 语言. (1996). Root. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Root.html 年

BibTeX

@misc{reference.wolfram_2024_root, author="Wolfram Research", title="{Root}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Root.html}", note=[Accessed: 27-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_root, organization={Wolfram Research}, title={Root}, year={2021}, url={https://reference.wolfram.com/language/ref/Root.html}, note=[Accessed: 27-November-2024 ]}