SecondOrderConeOptimization
SecondOrderConeOptimization[f,cons,vars]
二次錐および/または線形の制約 cons に従って線形目的関数 f を最小化する変数 vars の値を求める.
SecondOrderConeOptimization[c,{{a1,b1,α1,β1},…,{ak,bk,αk,βk}}]
制約条件![]() に従って
に従って ![]() を最小化するベクトル
を最小化するベクトル ![]() を求める.
を求める.
SecondOrderConeOptimization[c,…,{dom1,dom2,…}]
SecondOrderConeOptimization[…,"prop"]
どの解の特性"prop"を返すべきかを指定する.
詳細とオプション




- 二次錐最適化は,二次錐計画法(SOCP)および混合整数二次錐計画法(MISOCP)としても知られている.
- 二次錐最適化は,パラメータフィットや幾何学的距離問題等の問題に使われる.
- 二次錐最適化は,実変数,整数変数あるいは複素変数で大域的に効率よく解くことができる凸最適化問題である.
- 二次錐最適化は主問題を解く
 を求める.
を求める. -
最小化 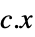
制約条件 ![TemplateBox[{{{{a, _, i}, ., x}, +, {b, _, i}}}, Norm]<=alpha_i.x+beta_i, i=1,..., k TemplateBox[{{{{a, _, i}, ., x}, +, {b, _, i}}}, Norm]<=alpha_i.x+beta_i, i=1,..., k](Files/SecondOrderConeOptimization.ja/7.png)
ただし 
- 混合整数の二次錐最適化は,問題を解く
 および
および 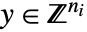 を求める.
を求める. -
最小化 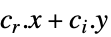
制約条件 ![TemplateBox[{{{{a, _, {(, {j, _, r}, )}}, ., x}, +, {{a, _, {(, {j, _, r}, )}}, ., {yb, _, j}}}}, Norm]<=alpha_(j_r).x+alpha_(j_i).y+beta_j, j=1,..., k TemplateBox[{{{{a, _, {(, {j, _, r}, )}}, ., x}, +, {{a, _, {(, {j, _, r}, )}}, ., {yb, _, j}}}}, Norm]<=alpha_(j_r).x+alpha_(j_i).y+beta_j, j=1,..., k](Files/SecondOrderConeOptimization.ja/12.png)
ただし 
- SecondOrderConeOptimizationは,目的関数が実数値のときは,内部的に実変数
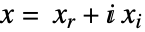 に変換して
に変換して ![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/SecondOrderConeOptimization.ja/15.png) の問題を解く.ただし,
の問題を解く.ただし, で
で 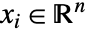 である.
である. - 変数指定 vars は,次のいずれかの形式で変数を与える要素のリストでなければならない.
-
v 名前が 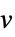 で次元が推測される変数
で次元が推測される変数v∈Reals 実数のスカラー変数 v∈Integers 整数のスカラー変数 v∈Complexes 複素数のスカラー変数 v∈ℛ 幾何学領域 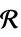 に制限されたベクトル変数
に制限されたベクトル変数v∈Vectors[n,dom] 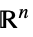 または
または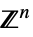 のベクトル変数
のベクトル変数v∈Matrices[{m,n},dom] 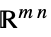 または
または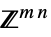 の行列変数
の行列変数 - 線形制約は二次制約を使って表されることがあるので注意こと.便宜上,単一の0は,必要に応じて,項が0の行列またはベクトルと解釈される.
-
{ai,bi,0,0} 線形等式制約 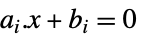
{0,0,αi,βi} 線形不等式制約 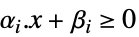
- 制約条件 cons は以下で指定できる.
-
LessEqual 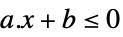
スカラー不等式 GreaterEqual 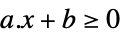
スカラー不等式 VectorLessEqual 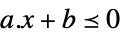
ベクトル不等式 VectorGreaterEqual 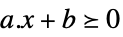
ベクトル不等式 Equal 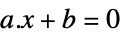
スカラー等式またはベクトル等式 Element 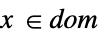
凸領域または領域要素 - SecondOrderConeOptimization[f,cons,vars]のとき,parval の形のパラメータ方程式が制約条件に含まれて,f または cons で使われるパラメータを定義することがある.ただし,par は vars には含まれず,val は数値または数値配列である.
- 主最小化問題はラグランジュの双対問題である最大化問題に関連している.双対最大値は常に主最小値以下なので,下限を与える.双対マキシマイザは,最小値の制約条件の変化に対する感度を含む主問題についての情報を与える.
- 二次錐最適化は双対を持つ. » »
-
最大化 
制約条件 ![sum_(i=1)^k(a_i.y_i+alpha_ilambda_i)⩵c, ; TemplateBox[{{y, _, i}}, Norm]<=lambda_i, i=1,..., k sum_(i=1)^k(a_i.y_i+alpha_ilambda_i)⩵c, ; TemplateBox[{{y, _, i}}, Norm]<=lambda_i, i=1,..., k](Files/SecondOrderConeOptimization.ja/34.png)
ただし 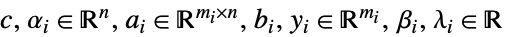
- 二次錐最適化では,強双対性が常に成り立つ.つまり,主最小化問題に解があれば双対最大化問題にも解があり,双対最大値と主最小値は等しい.
- 次は,可能な解の特性"prop"である.
-
"PrimalMinimizer" 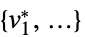
目的関数を最小化する変数値のリスト "PrimalMinimizerRules" 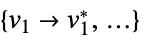
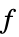 を最小化する変数の値 vars={v1,…}
を最小化する変数の値 vars={v1,…} "PrimalMinimizerVector" 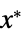
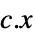 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 
最小値 
"DualMaximizer" 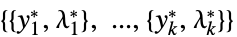
双対ベクトルの最大化 "DualMaximumValue" 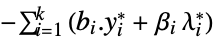
双対最大化の値 "DualityGap" 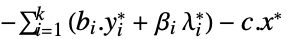
双対最適値と主最適値の差 "Slack" 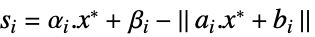
不等式制約を等式制約に変換するベクトル "ConstraintSensitivity" 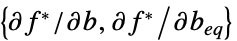
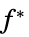 の制約摂動に対する感度
の制約摂動に対する感度"ObjectiveVector" 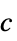
線形目的ベクトル "SecondOrderConeConstraints" 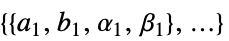
制約条件の係数のリスト "LinearEqualityConstraints" 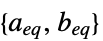
線形等式制約の行列とベクトル {"prop1","prop2",…} 複数の解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの局面について最適化するか Tolerance Automatic 内部比較に使用する許容度 - オプションMethod->method を使って使用するメソッドを指定することができる.次は使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する "SCS" SCS(錐ソルバの分割)ライブラリ "CSDP" CSDP(COIN半定値計画)ライブラリ "DSDP" DSDP(半定値計画)ライブラリ "PolyhedralApproximation" 多面体を使った近似制約 "MOSEK" 商用MOSEK凸最適化ソルバ "Gurobi" 商用Gurobi線形・二次最適化ソルバ "Xpress" 商用Xpress線形・二次最適化ソルバ - 計算はMachinePrecisionに限られる.

例題
すべて開くすべて閉じる例 (4)
スコープ (27)
基本的な用法 (9)
解の特性"PrimalMinimiumValue"を使って最小化する値を得る:
制約条件![]() に従って,a と b についての定数パラメータ方程式を使って
に従って,a と b についての定数パラメータ方程式を使って ![]() を最小化する:
を最小化する:
VectorGreaterEqual () とVectorLessEqual ()を使って制約条件を指定する:
![]() に従って
に従って ![]() を最小化する.Inactive[Plus]を使って意図しないスレッディングを回避する:
を最小化する.Inactive[Plus]を使って意図しないスレッディングを回避する:
行列 ![]() とベクトル
とベクトル ![]() をパラメータ化された方程式として指定してInactiveの使用を避ける:
をパラメータ化された方程式として指定してInactiveの使用を避ける:
![]() に従って
に従って ![]() を最小化する.NonNegativeRealsを使って制約条件
を最小化する.NonNegativeRealsを使って制約条件 ![]() を指定する:
を指定する:
整数変数 (4)
Integersを使って整数領域制約を指定する:
Vectors[n,Integers]を使ってベクトル変数についての整数領域制約を指定する:
NonNegativeIntegers (![]() )を使って非負の整数領域制約を指定する:
)を使って非負の整数領域制約を指定する:
NonPositiveIntegers (![]() )を使って非正の整数領域制約を指定する:
)を使って非正の整数領域制約を指定する:
複素変数 (4)
主モデルの特性 (3)
双対モデルの特性 (3)
オプション (8)
アプリケーション (35)
基本的なモデリング変換 (11)
![]() に従って
に従って ![]() を最大化する.目的関数を否定して最大化問題を解く:
を最大化する.目的関数を否定して最大化問題を解く:
制約条件 ![]() に従って
に従って ![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使って,
を使って,![]() に従って
に従って![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
制約条件 ![]() に従って
に従って ![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
![]() に従って
に従って![]() を最小化する.2つの補助変数
を最小化する.2つの補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
![]() に従って
に従って![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
SecondOrderConeOptimizationはAbsについての変換を直接行う:
制約条件 ![]() に従って
に従って![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
SecondOrderConeOptimizationはAbsについての変換を直接行う:
![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使い,制約条件
を使い,制約条件![]() に従って
に従って![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
制約条件でAbsを直接使うことで,計算が速くなり確度が高くなる:
![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使い,制約条件
を使い,制約条件![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
![]() に従って
に従って ![]() を最小化する.ただし,
を最小化する.ただし,![]() は非減少関数で,代りに
は非減少関数で,代りに ![]() を最小化する.主ミニマイザ
を最小化する.主ミニマイザ ![]() はどちらの問題についても同じままである.
はどちらの問題についても同じままである.![]() に従って
に従って ![]() を最小化することを考える:
を最小化することを考える:
幾何問題 (6)
半径1で中心が(0,0)と(2,1)の2つの円板の間の距離を最小化する.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
![]() を
を![]() 上の点,
上の点,![]() を
を![]() 上の点とする.目的は
上の点とする.目的は![]() を最小化することである.補助変数
を最小化することである.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
![]() を
を![]() 上の点,
上の点,![]() を
を![]() 上の点とする.目的は
上の点とする.目的は![]() を最小化することである.補助変数
を最小化することである.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
分離超平面定理によると,制約条件![]() に関連する双対は超平面の法線を与える:
に関連する双対は超平面の法線を与える:
制約条件 ![]() の内部構造は
の内部構造は![]() である.
である.![]() は行列
は行列 ![]() を含む唯一の制約条件である:
を含む唯一の制約条件である:
![]() を
を![]() 上の点,
上の点,![]() を
を![]() 上の点とする.目的は
上の点とする.目的は![]() を最小化することである.補助変数
を最小化することである.補助変数 ![]() を使い,
を使い,![]() に従って
に従って ![]() を最小化するものに問題を変換する:
を最小化するものに問題を変換する:
分離超平面定理によると,制約条件![]() に関連する双対は超平面の法線を与える:
に関連する双対は超平面の法線を与える:
制約条件 ![]() の内部形式は
の内部形式は ![]() である.
である.![]() は行列
は行列 ![]() を含む唯一の制約条件である:
を含む唯一の制約条件である:
最小包含円はBoundingRegionを使って効率よく求めることができる:
指定された領域を包み込む最小包含球の半径 ![]() と中心
と中心 ![]() を求める:
を求める:
最小包含球はBoundingRegionを使って効率よく求めることができる:
施設配置問題 (3)
ある会社が新たな工場を建設しようとしている.工場は5つの倉庫からの材料を必要とする.新規工場と倉庫の間の単位距離あたりの輸送費用は以下の通りである:
![]() を工場と倉庫
を工場と倉庫 ![]() の間の距離とする.目的は
の間の距離とする.目的は![]() を最小化することである:
を最小化することである:
ある会社が新たな工場を2つ建設しようとしている.この工場は5つの倉庫からの材料を必要とする.新規工場と倉庫の間の単位距離あたりの輸送費用は以下の通りである:
![]() を工場
を工場 ![]() と倉庫
と倉庫 ![]() の間の距離とする.目的は
の間の距離とする.目的は![]() を最小化することである:
を最小化することである:
会社の5つの小売店に商品を供給するために建設すべき最小数の倉庫とその場所を求める.候補地は5つある.ある倉庫からある小売店までの製品1単位の輸送コストは以下の表で与えられる:
倉庫 ![]() から小売店
から小売店 ![]() に輸送する単位数を
に輸送する単位数を ![]() とする.需要制約は以下の通りである:
とする.需要制約は以下の通りである:
![]() を,
を,![]() なら倉庫
なら倉庫 ![]() を建築するバイナリ決定ベクトルとする.供給制約は以下の通りである:
を建築するバイナリ決定ベクトルとする.供給制約は以下の通りである:
データフィッティング問題 (6)
制約条件 ![]() に従って
に従って![]() を最小化することで,離散データに対する線形フィットを求める:
を最小化することで,離散データに対する線形フィットを求める:
![]() を最小化することで離散データに対する五次多項式をフィットする:
を最小化することで離散データに対する五次多項式をフィットする:
DesignMatrixを使って入力データ行列を構築する:
最初と最後の点が同じ曲線上となるように,基底![]() を使ってノイズの多いデータの近似関数を求める:
を使ってノイズの多いデータの近似関数を求める:
![]() を最小化することで離散データへの強力な線形フィットを求める.ただし,
を最小化することで離散データへの強力な線形フィットを求める.ただし,![]() は既知の正規化パラメータである:
は既知の正規化パラメータである:
直線のプロットはこれが外れ値に対して強力であることを示している:
強力な ![]() フィットは関数Fitを使っても得ることができる:
フィットは関数Fitを使っても得ることができる:
過度の正規化を行うとフィットがデータに対して徐々に無感覚になる:
濃度で制約された最小二乗問題.![]() が最大で
が最大で ![]() 個の非零要素を持つように
個の非零要素を持つように![]() を最小化する:
を最小化する:
![]() が,もし
が,もし ![]() ならば
ならば ![]() は非零となるような決定ベクトルであるとする.決定制約は次のようになる:
は非零となるような決定ベクトルであるとする.決定制約は次のようになる:
![]() のときの制約
のときの制約 ![]() をモデル化するために,
をモデル化するために,![]() となるような大きい定数
となるような大きい定数 ![]() を選ぶ:
を選ぶ:
エピグラフ変換を使うと,目的は![]() に従って
に従って ![]() を最小化することになる:
を最小化することになる:
部分集合の選択は,Fitで ![]() 正規化を使うとより効率よくできる.まず,最高で
正規化を使うとより効率よくできる.まず,最高で ![]() 個の基底関数を使う正規化パラメータの範囲を求める:
個の基底関数を使う正規化パラメータの範囲を求める:
関数集合候補から与えられたデータを近似する関数の最良の部分集合を求める:
選択されなかった関数に関連付けられた係数は0でなければならない:
分類問題 (2)
構造最適化問題 (1)
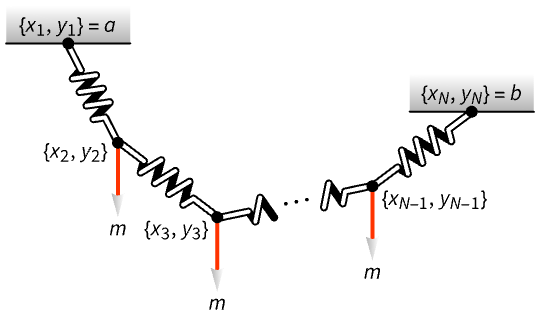
各リンクの端点における垂直荷重の下の ![]() のバネリンクで形成された吊り鎖の形状を求める.目的は,リンクの位置
のバネリンクで形成された吊り鎖の形状を求める.目的は,リンクの位置 ![]() を求めることである:
を求めることである:
重力によるポテンシャルエネルギーは![]() である.ただし,
である.ただし,![]() は各端点における垂直荷重で
は各端点における垂直荷重で ![]() は重力ある:
は重力ある:
伸長によるバネリンクの張力によるポテンシャルエネルギーは![]() である.ただし,
である.ただし,![]() はバネリンク
はバネリンク ![]() の伸長,
の伸長,![]() はバネの剛性である.
はバネの剛性である.![]() を使うと,エネルギーは
を使うと,エネルギーは ![]() に変換される:
に変換される:
結ばれたチェーンの端点は位置(0,0)と(2,-1)で固定されている:
各リンクは制約条件![]() を満足しなければならない.ただし,
を満足しなければならない.ただし,![]() は各バネの静止長である:
は各バネの静止長である:
ポートフォリオの最適化 (1)
リスクが最小でリターンか最大になるような,資本の6つの株式への投資配分を求める:
株式 ![]() への投資の全投資に占める割合を
への投資の全投資に占める割合を ![]() としよう.リターンは
としよう.リターンは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は個別の株式の予想収益の値のベクトルである:
は個別の株式の予想収益の値のベクトルである:
リスクは ![]() で与えられる.
で与えられる.![]() はリスク回避パラメータであり,
はリスク回避パラメータであり,![]() である:
である:
目標は,指定されたリスク回避パラメータについてリスクを最小にしつつリターンを最大にすることである:
投資 ![]() の割合はすべて0より大きく1に加えられなければならない:
の割合はすべて0より大きく1に加えられなければならない:
リスク回避パラメータの範囲内でリターンと対応するリスクを計算する:
範囲 ![]() における最適値
における最適値 ![]() は,リスクとリターンのトレードオフにおける上包を与える:
は,リスクとリターンのトレードオフにおける上包を与える:
非負行列因子分解 (1)
投資問題 (3)
最低でも1000ドルの配当が得られリスクが最小となるように,資本金10000ドルを4つの株に割り当てる方法を求める.期待する戻り値と株式に関連付けられた共分散行列 ![]() は次の通りである:
は次の通りである:
4つの株の単価は1ドルである.各株には最大で2500ドルを割り当てることができる:
エピグラフ変換を使うと,![]() で与えられるリスクが制約に変換される:
で与えられるリスクが制約に変換される:
各株式に費やす金額の送料は,以下で与えられるリスクを最小にすることで求められる:
空売りオプションも含めて最低でも配当が1000ドルになるようにし,リスクが最小となるようにして,4つの株式から買う株の数を求める:
資本金についての制約,投資に対する配当の制約,リスク制約は次の通りである:
空売りオプションを使用すると株が売却できる.目的関数 ![]() によって与えられるリスクを最小化することで,買う/空売りする株式の最適数がもとまる:
によって与えられるリスクを最小化することで,買う/空売りする株式の最適数がもとまる:
2番目の株式は空売りすることができる.空売りで最低1000ドル得るための総投資額は以下の通りである:
空売りをしなければ,初期投資ははるかに大きくなければならない:
リスクを最小限に抑えながら収益を最大化するために,可能性のある20の候補株の中から投資する6つの株の最適な組合せを求める:
![]() を株式
を株式 ![]() で行われた総投資の割合とする.利益は
で行われた総投資の割合とする.利益は ![]() で与えられる.ここで,
で与えられる.ここで,![]() は各株式の期待利益値のベクトルである:
は各株式の期待利益値のベクトルである:
リスクは ![]() で与えられる.
で与えられる.![]() はリスク回避パラメータであり,
はリスク回避パラメータであり,![]() である:
である:
目的は,利益を最大にしつつ指定のリスク回避パラメータについてリスクを最小にすることである:
![]() を,
を,![]() であれば株式を購入する決定ベクトルとする.6つの株式を選ばなければならない:
であれば株式を購入する決定ベクトルとする.6つの株式を選ばなければならない:
特性と関係 (8)
SecondOrderConeOptimizationは,目的関数の大域的最小値を与える:
Minimizeは,二次最適化問題の大域的厳密結果を与える:
NMinimizeを使い,大域メソッドを使って近似結果を得ることができる:
FindMinimumを使い,局所メソッドを使って近似結果を得ることができる:
LinearOptimizationはSecondOrderConeOptimizationの特殊ケースである:
QuadraticOptimizationはSecondOrderConeOptimizationの特殊ケースである:
SemidefiniteOptimizationはSecondOrderConeOptimizationの一般化である:
考えられる問題 (5)
厳密な不等式を使って指定された制約条件は,メソッドによっては満足されないことがある:
理由は,SecondOrderConeOptimizationが![]() を解くからである:
を解くからである:
ミニマイザはIndeterminateである:
ミニマイザはIndeterminateである:
混合整数問題に対する双対に関連した解の特性は得られないかもしれない:
複素数値を含む制約条件はベクトル不等式で指定しなければならない:
両辺が理論的に実数の場合でも,Lessを使うだけではうまくいかない:
テキスト
Wolfram Research (2019), SecondOrderConeOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/SecondOrderConeOptimization.html (2020年に更新).
CMS
Wolfram Language. 2019. "SecondOrderConeOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/SecondOrderConeOptimization.html.
APA
Wolfram Language. (2019). SecondOrderConeOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SecondOrderConeOptimization.html