Series

Series[f,{x,x0,n}]

f の(x-x0)n次までの点 x=x0に関するベキ級数展開を作成する．ただし，n は明示的な整数である．

Series[f,xx0]

f についての点 x=x0の周りのベキ級数展開における最高次の項を生成する．

Series[f,{x,x0,nx},{y,y0,ny},…]

x に関するベキ級数展開を作成し，次に y に関するという具合に継続して展開する．

詳細とオプション

  • Seriesは，標準的なテイラー(Taylor)級数や，特定の負のベキ，分数ベキ，そして対数が関わる展開を構築することができる．
  • Seriesは，ある種の真性特異点を求めることができる．On[Series::esss]とすると，この場合にSeriesがメッセージを生成するようになる．
  • Seriesは，点 x=∞について展開することもできる．
  • Series[f,{x,0,n}]は，任意の関数 f のテイラー級数を公式 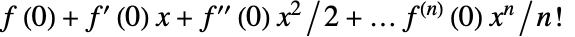に従って構築する．
  • Seriesは，Dを使って偏微分を評価する．それぞれの変数は独立であることを前提とする．
  • Seriesの結果は，SeriesDataオブジェクトで，他の関数を使ってこれを操作することができる．
  • Normal[series]はベキ級数を切断し通常式へ変換する．
  • SeriesCoefficient[series,n]は，n 次項の係数を求める．
  • 次は，使用可能なオプションである．
  • Analytic True認識されない関数を解析的なものとして扱うかどうか
    Assumptions $Assumptionsパラメータについての仮定
    SeriesTermGoalAutomatic近似における項数

例題

すべて開くすべて閉じる

例  (4)

近傍における指数関数のベキ級数：

通常の式に変換する：

近傍における任意関数のベキ級数：

級数にどのような操作をしても，適切な項だけが残される：

ベキ級数の最高次の項を求める：

スコープ  (10)

一変数級数  (10)

Seriesは分数ベキや対数が扱える：

記号的なパラメータがしばしば用いられる：

負のベキを持つローラン(Laurent)級数を生成することができる：

指定された負のベキになるように級数を切り詰める：

特殊関数のベキ級数を求める：

分岐点で関数の級数を求める：

xが分岐点の左側だと仮定すると，より簡単な結果が返される：

区分関数：

無限大におけるベキ級数：

Seriesが漸近級数を与えることがある：

方程式の陰解の級数展開：

評価されていない積分の級数展開：

一般化と拡張  (4)

二変数のベキ級数：

Seriesは要素単位でリストに並列的な関数の適用を行う：

SeriesはSeriesData式を生成する：

Seriesは近似数を扱うことができる：

オプション  (4)

Analytic  (1)

デフォルトで，Seriesは記号的関数が解析的であると仮定する：

Assumptions  (3)

Assumptionsを使って展開が適用される複素平面の領域を指定する：

仮定がないと，区分関数が現れる：

Stokes領域で展開する：

アプリケーション  (8)

の連続的な級数近似をプロットする：

標準的な組合せ問題の級数展開を求める：

母関数からフィボナッチ(Fibonacci)数を求める：

母関数を展開することでルジャンドル(Legendre)多項式を求める：

アメリカ合衆国の硬貨を使って両替する方法を列挙する母関数を設定する：

1ドルの両替の仕方の数：

大きい多項式の最低次数項を求める：

近傍での f[x]の根のニュートン近似におけるより高次数の項を求める：

Exp[x]の級数近似の複素零点をプロットする：

特性と関係  (10)

Seriesは常に項を指定の次数までにとどめる：

級数を操作すると適切な項だけが残される：

Normalは通常の多項式に変換する：

級数には任意の数学関数が適用できる：

低次数の級数を加えると高次数の項が除去される：

級数を微分する：

級数の係数について方程式を解く：

級数中の係数のリストを求める：

O[x]を使って強制的に級数を構築する：

ComposeSeriesは，級数を他の級数に適用する関数として扱う：

InverseSeriesは，級数の逆関数の級数を求めるために級数を逆にする：

FunctionAnalyticを使って関数が解析的かどうかを調べる：

解析的関数は，その定義域内の各点でテイラー級数として表すことができる：

結果の多項式は0近くで を近似する：

考えられる問題  (7)

真性特異点があると，Seriesはこれを因数分解しようとする：

級数中の展開変数に関しては，数値を直接代入することはできない：

Normalを使って代入が可能な普通の式を求める：

級数はプロットする前に普通の式に変換しなければならない：

異なる展開点を持つベキ級数は結合することはできない：

すべての級数が頭部SeriesDataを持つ式で表される訳ではない：

関数の中にはベキのような関数の級数に分解できないものもある：

Seriesは展開変数と無関係な式は変えない：

Wolfram Research (1988), Series, Wolfram言語関数， https://reference.wolfram.com/language/ref/Series.html （2020年に更新）.

テキスト

Wolfram Research (1988), Series, Wolfram言語関数， https://reference.wolfram.com/language/ref/Series.html （2020年に更新）.

CMS

Wolfram Language. 1988. "Series." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Series.html.

APA

Wolfram Language. (1988). Series. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Series.html

BibTeX

@misc{reference.wolfram_2024_series, author="Wolfram Research", title="{Series}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Series.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_series, organization={Wolfram Research}, title={Series}, year={2020}, url={https://reference.wolfram.com/language/ref/Series.html}, note=[Accessed: 21-November-2024 ]}