Series

Series[f,{x,x0,n}]

生成 f 关于点 x=x0 的幂级数展开式，最高次数为 (x-x0)n，其中 n 是显式整数.

Series[f,xx0]

生成 f 关于点 x=x0 的幂级数展开式的首项.

Series[f,{x,x0,nx},{y,y0,ny}]

求出连续的先关于 x 然后关于 y 的幂级数展开式.

更多信息和选项

  • Series 可以建立标准的泰勒级数，以及包含负数次幂、分数次幂和对数的特定展开式.
  • Series 检测奇点. On[Series::esss] 使 Series 产生关于奇点的信息.
  • Series 可在点 x=∞ 处展开.
  • 根据公式 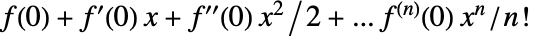，Series[f,{x,0,n}] 构造任意函数 f 的泰勒展开式.
  • Series 用 D 有效地计算偏导数. 它假定不同的变量是独立的.
  • Series 的结果通常是一个可以在其它函数中处理的 SeriesData 对象.
  • Normal[series] 截取幂级数并把它转换为一个普通表达式.
  • SeriesCoefficient[series,n] 求出 n 次项的系数.
  • 可给出以下选项：
  • Analytic True是否将无法识别的函数视为解析函数
    Assumptions $Assumptions关于参数的假设
    SeriesTermGoalAutomatic近似式的项数

范例

打开所有单元关闭所有单元

基本范例  (4)

指数函数关于 的幂级数：

转换为普通表达式：

任意函数关于 的幂级数：

在级数的一些操作中，仅保留适当项：

求幂级数的首项：

范围  (10)

单元系列  (10)

Series 可以处理分数幂和对数：

通常使用符号参数：

产生负数次幂的 Laurent 级数：

按指定的负数幂截取级数：

求出特定函数的幂级数：

求出函数在分支点的级数：

当 x 假设位于分支点的左边，给出一个简单的结果：

分段函数：

在无穷处的幂级数：

Series 可以给出渐近线级数：

方程隐式解的级数展开：

不计算的积分的级数展开：

推广和延伸  (4)

二元幂级数：

Series 按元素线性作用于列表：

Series 产生 SeriesData 表达式：

Series 可以作用于近似数：

选项  (4)

Analytic  (1)

缺省下 Series 假设函数是解析的：

Assumptions  (3)

用 Assumptions 指定应用展开的复平面上的区域：

无假设时，分段函数的显示：

在 Stokes 区域上获得级数：

应用  (8)

绘制近似于 的连续级数：

求出标准复合问题的级数展开：

从生成函数中求出 Fibonacci 数：

通过展开生成函数求出 Legendre 多项式：

用 U.S. coins 建立一个生成函数，列举改变的方式：

关于 $1 改变方式的数量：

在较长多项式中求出最低项：

用牛顿近似法求出 f[x] 在 周围的高次项：

绘制近似 Exp[x] 的级数的零：

属性和关系  (10)

Series 通常将项保持到指定次数为止：

级数的操作仅对适当的项起作用：

Normal 转换为普通多项式：

任何数学函数可以应用到级数中：

增加低次项会导致高次项的丢失：

级数的微分：

求解级数系数的方程：

求出级数中系数的列表：

用 O[x] 强调级数的构建：

ComposeSeries 将一个级数作为一个函数，应用到另一个级数中：

InverseSeries 执行级数的逆操作，求出级数逆函数的级数：

使用 FunctionAnalytic 检验函数是否为解析函数：

解析函数可以在其定义域的每个点上表示为泰勒级数：

所得的多项式在 0 附近逼近 ：

可能存在的问题  (7)

当存在奇点，Series 将尽可能的因式分解：

数值量不能直接被级数中展开变量替代：

用 Normal 获取可以执行替代的普通表达式：

在绘制前，级数必须转换为普通表达式：

不同展开点的幂级数不能组合：

不是所有级数可以用有头部 SeriesData 的表达式来表示：

某些函数不能分解成类幂函数的级数：

Series 没有改变独立于扩展变量的表达式：

Wolfram Research (1988)，Series，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Series.html （更新于 2020 年）.

文本

Wolfram Research (1988)，Series，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Series.html （更新于 2020 年）.

CMS

Wolfram 语言. 1988. "Series." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/Series.html.

APA

Wolfram 语言. (1988). Series. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Series.html 年

BibTeX

@misc{reference.wolfram_2024_series, author="Wolfram Research", title="{Series}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Series.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_series, organization={Wolfram Research}, title={Series}, year={2020}, url={https://reference.wolfram.com/language/ref/Series.html}, note=[Accessed: 21-November-2024 ]}