ShortTimeFourier[data]
returns the short-time Fourier transform (STFT) of data as a ShortTimeFourierData object.
ShortTimeFourier[data,n]
uses partitions of length n.
ShortTimeFourier[data,n,d]
uses partitions with offset d.
ShortTimeFourier[data,n,d,wfun]
applies a smoothing window wfun to each partition.
ShortTimeFourier[data,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.


ShortTimeFourier
ShortTimeFourier[data]
returns the short-time Fourier transform (STFT) of data as a ShortTimeFourierData object.
ShortTimeFourier[data,n]
uses partitions of length n.
ShortTimeFourier[data,n,d]
uses partitions with offset d.
ShortTimeFourier[data,n,d,wfun]
applies a smoothing window wfun to each partition.
ShortTimeFourier[data,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.
Details and Options

- The short-time Fourier transform (STFT) is a time-frequency representation of a signal and is typically used for transforming, filtering and analyzing the signal in both time and frequency.
- ShortTimeFourier[data] computes the discrete Fourier transform (DFT) of partitions of data and returns a ShortTimeFourierData object.
- Use Spectrogram on data or on the resulting ShortTimeFourierData object to plot the spectrogram.
- ShortTimeFourier[data] uses partitions of length
![n=2^Round[InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True](sqrt(m))+1] n=2^Round[InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True](sqrt(m))+1]](Files/ShortTimeFourier.en/2.png) and offset
and offset ![d=Round[n/3] d=Round[n/3]](Files/ShortTimeFourier.en/3.png) , where
, where 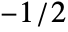 is Length[data].
is Length[data]. - The partition length n and offset d can be expressed as integer numbers (interpreted as number of samples) or as time or sample quantities.
- If necessary, fixed padding is used on the right to make all the partitions the same size.
- In ShortTimeFourier[data,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between
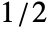 and
and 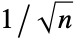 or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
or a list of length n. The default window is DirichletWindow, which effectively does no smoothing. - The data can be any of the following:
-
list arbitrary rank numerical array audio an Audio or Sound object video a Video object - For multichannel audio objects, the spectrogram is computed over the sum of all channels.
- ShortTimeFourier accepts the FourierParameters option. The default setting is FourierParameters->{1,-1}.
Examples
open all close allBasic Examples (2)
Scope (7)
Data (3)
Parameters (4)
By default, an automatic partition size is used:
Specify the number of samples in each partition:
Specify the partition size using a time Quantity:
By default, an automatic partition offset is used:
Specify the offset using the number of samples:
Specify the offset using a time Quantity:
Use Scaled to specify offset relative to the partition size:
By default, no smoothing is applied to partitions:
Using None or DirichletWindow is equivalent to no smoothing:
Use a HannWindow as smoothing window function:
Use a precomputed list as smoothing window function:
By default, partitions are not padded:
Pad each partition to be 20 samples long:
Specify padding using a time Quantity:
Applications (6)
Compute the full short-time Fourier transform of a signal:
Plot of the magnitude of the ShortTimeFourier data:
Apply a smoothing window function:
Magnitude spectrum of a single partition:
Compute the full short-time Fourier transform of a signal:
Compute the magnitude spectrogram:
Compute the power spectrogram:
Compute the power spectrogram in decibels:
Compute the forward and inverse short-time Fourier transform of a signal:
Compute the short-time Fourier transform:
Approximate the inverse using InverseShortTimeFourier:
Compute the full short-time Fourier transform of the signal:
Define a nonlinear function to squash low-amplitude components:
Apply the function to the short-time Fourier transform data:
Invert the short-time Fourier transform using InverseShortTimeFourier:
Change the speed of an audio recording using different STFT partition offsets:
Change the "PartitionOffset" property:
Compute the inverse short-time Fourier transform to speed up the recording:
Slow down an audio signal by resampling the short-time Fourier transform:
Compute the inverse short-time Fourier transform to get a slowed-down version of the original:
Properties & Relations (2)
Short-time Fourier transform data is the same as the values computed by SpectrogramArray:
Spectrogram of the ShortTimeFourier is equivalent to Spectrogram of the original signal:
Notice that the default partitioning parameters are different:
Text
Wolfram Research (2019), ShortTimeFourier, Wolfram Language function, https://reference.wolfram.com/language/ref/ShortTimeFourier.html (updated 2024).
CMS
Wolfram Language. 2019. "ShortTimeFourier." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ShortTimeFourier.html.
APA
Wolfram Language. (2019). ShortTimeFourier. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShortTimeFourier.html
BibTeX
@misc{reference.wolfram_2025_shorttimefourier, author="Wolfram Research", title="{ShortTimeFourier}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ShortTimeFourier.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_shorttimefourier, organization={Wolfram Research}, title={ShortTimeFourier}, year={2024}, url={https://reference.wolfram.com/language/ref/ShortTimeFourier.html}, note=[Accessed: 06-March-2026]}