ShortTimeFourier

ShortTimeFourier[data]

返回作为 ShortTimeFourierData 对象的 data 的短时傅立叶变换 (STFT).

ShortTimeFourier[data,n]

使用长度为 n 的部分.

ShortTimeFourier[data,n,d]

使用偏移量为 d 的部分.

ShortTimeFourier[data,n,d,wfun]

对每个分区应用平滑窗口 wfun.

ShortTimeFourier[data,n,d,wfun,m]

在计算变换前用零填充长度为 m 的分区.

更多信息和选项

  • 短时傅立叶变换 (STFT) 是信号的时频表示，一般用于变换、滤波和分析时域和频域的信号.
  • ShortTimeFourier[data] 计算 data 分区的离散傅立叶变换 (DFT) ，并返回一个 ShortTimeFourierData 对象.
  • 使用 data 上的 Spectrogram 或结果 ShortTimeFourierData 对象绘制频谱.
  • ShortTimeFourier[data] 使用长度为 n=2^Round[InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True](sqrt(m))+1] 的分区和偏移量 d=Round[n/3]，其中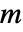， 是 Length[data].
  • 分区长度 n 和偏移量 d 可表示为整数（诠释为样本数）或作为时间或样本量.
  • 如果必要，使用固定的右填充使得所有分区具有同样的大小.
  • 在 ShortTimeFourier[data,n,d,wfun] 中，平滑窗口 wfun 可以使用窗口函数指定并在 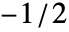和 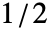间或长度为 n 的列表中采样. 默认窗口是 DirichletWindow，它没有平滑.
  • data 可以如下：
  • list任意阶的数值数组
    audio一个 Audio 或 Sound 对象
    videoVideo 对象
  • 对于多通道音频对象，频谱是在所有通道的和之上计算的.
  • ShortTimeFourier 接受 FourierParameters 选项. 默认设置是 FourierParameters->{1,-1}.

范例

打开所有单元关闭所有单元

基本范例  (2)

正弦波的短时傅立叶变换：

音频信号的短时傅立叶变换：

绘制结果：

范围  (7)

数据  (3)

音频录音的短时傅立叶变换：

数组的短时傅立叶变换：

视频的音轨的短时傅立叶变换：

参数  (4)

默认情况下，使用自动的分区大小：

指定每个分区的样本大小：

使用时间 Quantity 指定分区大小：

默认情况下，使用自动分区偏移：

使用样本数指定偏移：

使用时间 Quantity 指定偏移：

使用 Scaled 指定相对于分区大小的偏移：

默认情况下，没有对分区使用平滑：

使用 None 或 DirichletWindow 等价于没有平滑：

使用 HannWindow 作为平滑窗口函数：

使用预计算列表作为平滑窗口函数：

默认情况下，分区没有被填充：

把每个分区填充为 20 个样本长：

使用时间 Quantity 指定填充：

选项  (3)

FourierParameters  (3)

没有正则化：

正则化 ：

正则化 ：

应用  (6)

计算信号的完整短时傅立叶变换：

绘制 ShortTimeFourier 数据的幅度：

应用平滑窗口函数：

单个分区的幅度频谱：

计算信号的完整短时傅立叶变换：

计算幅度频谱：

计算功率频谱：

计算分贝的功率频谱：

计算信号的前向和逆短时傅立叶变换：

计算短时傅立叶变换：

使用 InverseShortTimeFourier 近似逆：

去噪啁啾信号：

计算信号的完整短时傅立叶变换：

定义侧滑 (squash) 低幅度分量：

把函数应用到短时傅立叶变换数据：

使用 InverseShortTimeFourier 求逆短时傅立叶变换：

使用不同的 STFT 分区偏移改变音频录音的速度：

改变 "PartitionOffset" 属性：

计算逆短时傅立叶变换加速录音：

通过重新采样短时傅立叶变换减缓音频信号：

重新采样数据：

计算逆短时傅立叶变换回去原始的减缓版本：

属性和关系  (2)

短时傅立叶变换数据与由 SpectrogramArray 计算的的值一样：

ShortTimeFourier 的 Spectrogram 等价于原始信号的 Spectrogram：

注意，默认的分区参数是不一样的：

Wolfram Research (2019)，ShortTimeFourier，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ShortTimeFourier.html （更新于 2024 年）.

文本

Wolfram Research (2019)，ShortTimeFourier，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ShortTimeFourier.html （更新于 2024 年）.

CMS

Wolfram 语言. 2019. "ShortTimeFourier." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/ShortTimeFourier.html.

APA

Wolfram 语言. (2019). ShortTimeFourier. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ShortTimeFourier.html 年

BibTeX

@misc{reference.wolfram_2024_shorttimefourier, author="Wolfram Research", title="{ShortTimeFourier}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ShortTimeFourier.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_shorttimefourier, organization={Wolfram Research}, title={ShortTimeFourier}, year={2024}, url={https://reference.wolfram.com/language/ref/ShortTimeFourier.html}, note=[Accessed: 05-November-2024 ]}