SparseArray

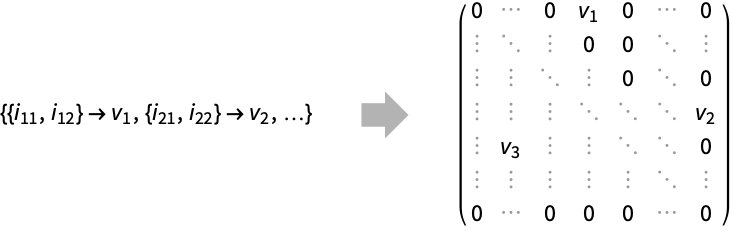
SparseArray[{pos1val1,pos2val2,…}]

yields a sparse array in which values vali appear at positions posi.

SparseArray[{pos1,pos2,…}{val1,val2,…}]

yields the same sparse array.

SparseArray[list]

yields a sparse array version of list.

SparseArray[data,{d1,d2,…}]

yields a sparse array representing a d1×d2×… array.

SparseArray[data,dims,val]

yields a sparse array in which unspecified elements are taken to have value val.

Details

  • By default, SparseArray takes unspecified elements to be 0.
  • SparseArray[data,…] is always converted to an optimized standard form with structure SparseArray[Automatic,dims,val,…].
  • Normal[SparseArray[…]] gives the ordinary array corresponding to a sparse array object.
  • ArrayRules[SparseArray[…]] gives the list of rules {pos1->val1,pos2->val2,…}.
  • The elements in SparseArray need not be numeric.
  • The position specifications posi can contain patterns.
  • SparseArray[{{i_,i_}->1},{d,d}] gives a d×d identity matrix.
  • Rules of the form Band[…]->vals specify values on bands in the sparse array.
  • With rules posi:>vali the vali are evaluated separately for each set of indices that match posi.
  • SparseArray[list] requires that list be a full array, with all parts at a particular level being lists of the same length.
  • The individual elements of a sparse array cannot themselves be lists.
  • SparseArray[rules] yields a sparse array with dimensions exactly large enough to include elements whose positions have been explicitly specified.
  • SparseArray[rules,Automatic,val] takes unspecified elements to have value val.
  • List and matrix operations are typically set up to work as they do on Normal[SparseArray[…]].
  • Functions with attribute Listable are automatically threaded over the individual elements of the ordinary arrays represented by SparseArray objects.
  • Part extracts specified parts of the array represented by a SparseArray object, rather than parts of the SparseArray expression itself.
  • Functions like Map are automatically applied to components in a SparseArray object.
  • SparseArray is treated as a raw object by functions like AtomQ and for purposes of pattern matching.
  • Dimensions gives the dimensions of a sparse array.
  • The standard output format for a sparse array indicates the number of nondefault elements and the total dimensions.

Examples

open allclose all

Basic Examples  (1)

Construct a sparse matrix with values at only a few specified positions:

View it as a matrix:

Convert it to an ordinary dense matrix:

Scope  (7)

Make a large sparse vector matrix and depth-3 array:

Construct a tridiagonal matrix using patterns for indices:

Construct a 10,000 by 10,000 version:

Make a sparse diagonal matrix:

This is equivalent to DiagonalMatrix:

Except that as a sparse matrix, it uses much less memory:

Construct a block diagonal matrix using rules with Band:

Convert an ordinary matrix into a sparse matrix:

Make a rank-4 sparse tensor with values at random positions:

ArrayRules produces the minimal list of rules needed to specify the SparseArray:

Many typical operations work with SparseArray objects as they would for equivalent lists:

Arithmetic works element-wise just as it does for lists:

Matrix products are done with Dot:

Many linear algebra functions are done efficiently with the sparse form:

Many other list commands work automatically:

Generalizations & Extensions  (2)

The unspecified elements can have any value:

Symbolic values can be replaced with local definitions:

Construct a sparse matrix with all machine-number values:

Construct a sparse matrix with exact integer values:

N[s] is the same as ns:

Applications  (4)

Create a list with a single nonzero element:

Plot a list of rules:

Represent a network with an adjacency matrix:

Solve a boundary-value problem using finite differences:

Properties & Relations  (3)

A SparseArray object is Equal to the corresponding ordinary list:

They are not SameQ because the expression structure is different:

For functions f that work with SparseArray objects, typically f[s]==f[Normal[s]]:

This includes all functions with the attribute Listable:

Convert linear expressions to SparseArray objects using CoefficientArrays:

Convert from SparseArray to expressions using Dot:

Possible Issues  (6)

If a position is repeated in the rule list for SparseArray, the first instance is used:

SparseArray objects can represent data too large to represent in normal form:

Using Normal will give a SystemException:

Sparse operations do not by default check for cancellation:

Use SparseArray to recompute the sparse structure:

Operations with side effects may give different values when iterating over SparseArray:

With Reap and Sow you can see what elements are accessed:

For a SparseArray object, Part gives parts of the represented list:

The FullForm is a way of reconstructing the object from basic storage information:

It should not be necessary, but if you want, you can get pieces of the full form with patterns:

A SparseArray object is treated as atomic for functions that do not work on the representation:

Cases does not work on the represented matrix:

You can often use the result of ArrayRules to get the information without expanding:

Neat Examples  (1)

The Game of Life:

Introduced in 2003
 (5.0)
 |
Updated in 2007
 (6.0)