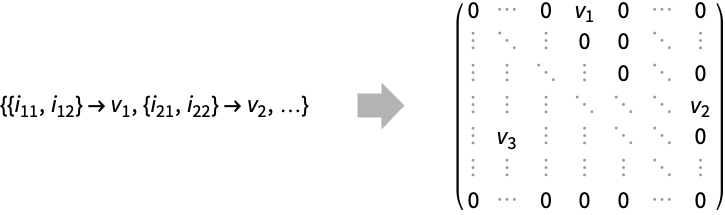
SparseArray[{pos1v1,pos2v2,…}]
位置 posiの値 viを除いてすべての要素が0である疎な配列を与える.
SparseArray[list]
list の疎な配列版を与える.
SparseArray[data,{d1,d2,…}]
d1×d2×… 配列を表す疎な配列を与える.
SparseArray[data,dims,val]
指定されていない要素は値 val を持つと解釈される疎な配列を与える.


SparseArray
SparseArray[{pos1v1,pos2v2,…}]
位置 posiの値 viを除いてすべての要素が0である疎な配列を与える.
SparseArray[list]
list の疎な配列版を与える.
SparseArray[data,{d1,d2,…}]
d1×d2×… 配列を表す疎な配列を与える.
SparseArray[data,dims,val]
指定されていない要素は値 val を持つと解釈される疎な配列を与える.
詳細



- SparseArrayは疎な行列としても知られている.
- 疎な配列は,通常,ほとんどの項目が0の効率的な線形代数やグラフ隣接行列で使われる.
- 疎な配列は非零の値がある位置だけを保存するが配列全体を表す.
- data は次の形式でよい.
-
rules 位置と値を指定する規則 list 配列をSparseArray に変換する SymmetrizedArray[…] SparseArrayに変換する QuantityArray[…] QuantityのSparseArray に変換する SparseArray[…] 明示的な非零要素を最小にする - s=SparseArray[rules,…]のときは以下の指定を使うことができる.
-
{{i1 1,…,i1 r}v1,{i2 1,…,i2 r}v2,…} s[[i1 1, …, i1 r]]は値v1を,s[[i2 1, …, i2 r]]は値 v2を持つ等 pattv パターン patt に一致する{ik 1,…,ik r}すべてについて{{i1 1,…,i1 r}v,{i2 1,…,i2 r}v,…} patt:>v 一致する各位置について値 v を評価する Band[…]vals 帯と部分ブロックについて値を指定する {pos1,pos2,…}{v1,v2,…} {pos1v1,pos2v2,…}に等しい - 以下は,SparseArray変換である.
-
Normal[SparseArray[…]] 通常のList配列に変換する SymmetrizedArray[SparseArray[…]] 対称化された配列に変換する ArrayRules[SparseArray[…]] 規則のリスト{pos1->v1,pos2->v2,…}を与える - SparseArrayオブジェクトは通常の配列の表現なので,多くの関数が通常の配列と同じように扱う.例として,Dimensions,Part,Plus,LinearSolve等の関数が挙げられる.
- SparseArray[data,…]はSparseArray[Automatic,dims,val,…]という構造の最適化された標準形に常に変換される.
- SparseArrayは,AtomQのような関数によってあるいはパターンマッチングの目的では,生のオブジェクトとして扱われる.
- デフォルトで,SparseArrayは指定されていない要素 val は0であるとみなす.
- SparseArrayの要素は数値ではなくてもよいが,それ自体がリストであってはならない.
- SparseArray[…][prop]はSparseArrayオブジェクトの特性 prop を与える.次は,使用可能な特性である.
-
"ImplicitValue" 明示的には与えられていない要素の値を与える "ExplicitLength" 明示的な値の数を与える "ExplicitValues" 明示的な値のリストを与える "ExplicitPositions" 明示的な値に対応する位置のリストを与える "ColumnIndices" 圧縮された疎な行による表現からの列の指標を与える "RowPointers" 圧縮された疎な行による表現からの行のポインタリストを与える "BandWidth" 疎な行列についてのオフ対角帯幅を与える "Density" 要素の総数に対する明示的な値の割合を与える
例題
すべて開く すべて閉じるスコープ (7)
これはDiagonalMatrixに等しい:
Bandの規則を用いてブロック対角行列を作る:
ArrayRulesはSparseArrayを指定するのに必要最低限の規則のリストを作る:
多くの一般的な演算では,SparseArrayオブジェクトはそれと同等のリストと同じように扱われる:
行列の積はDotで計算される:
一般化と拡張 (2)
特性と関係 (3)
SparseArrayオブジェクトは対応する一般的なリストに等しい(Equal):
式の構造が異なるので,これらはSameQではない:
SparseArrayオブジェクトと使われる関数 f については,一般に f[s]==f[Normal[s]]である:
これは,属性がListableのすべての関数を含む:
CoefficientArraysを使って線形の式をSparseArrayオブジェクトに変換する:
Dotを使ってSparseArrayから式に変換する:
考えられる問題 (9)
SparseArrayの規則のリストである位置が繰り返される場合は,最初のものが使われる:
SparseArrayオブジェクトは,一般の形式では表現できないほど大きいデータでも表すことができる:
Normalを使うとSystemExceptionが返される:
SparseArrayを使って疎な構造を再計算する:
SparseArray表現の内部構造は一意的ではなく,SameQはこれを検出する:
SparseArrayを使って疎な構造を再計算する:
Equalが予想通りに動作することに注意のこと:
SparseArray表現の内部構造は一意的ではなく,部分的な設定でその構造が変わる可能性がある:
SparseArrayの例が等しいかどうかをテストする:
SparseArrayを使って疎な構造を再計算する:
Equalが予想どうりに動作する点に注意のこと:
副次的な影響のある操作をSparseArrayに繰り返し使うと異なる結果が返されることがある:
ReapとSowを使ってどの要素がアクセスされているかを見ることができる:
SparseArrayオブジェクトについて,Partは表されたリストの部分を返す:
FullFormは基本的な保存情報からオブジェクトを再構成する方法である:
表現に作用しない関数については,SparseArrayオブジェクトは原子的なものとして扱われる:
表示された行列にはCasesは使えない:
ArrayRulesの結果を使って展開せずに情報を得られることがよくある:
密なSparseArrayの場合でも,0による除算が可能なことがある:
SparseArrayの密度は1である:
密度が1なので,このSparseArrayは非常に特殊なケースであり,この作業を行うには計算量が膨大になる.この場合は行列が密なのでNormalの使用が正当化される:
関連項目
ArrayRules SparseArrayQ Normal Band CoefficientArrays ArrayPlot Array ConstantArray NumericArray Association
Function Repository: SparseAssociation
テクニカルノート
関連するガイド
-
▪
- 疎な(スパース)配列 ▪
- 行列の構成 ▪
- 行列と線形代数 ▪
- リストの構築 ▪
- テンソル ▪
- グラフと行列 ▪
- ベクトル操作 ▪
- 構造化行列とたたみ込みカーネル ▪
- 3D画像 ▪
- リスト操作 ▪
- データの配列の操作 ▪
- 系のモデル化 ▪
- 線形・非線形フィルタ
関連するワークフロー
- 行列を作成する
履歴
2003 で導入 (5.0) | 2007 で更新 (6.0) ▪ 2021 (13.0)
テキスト
Wolfram Research (2003), SparseArray, Wolfram言語関数, https://reference.wolfram.com/language/ref/SparseArray.html (2021年に更新).
CMS
Wolfram Language. 2003. "SparseArray." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/SparseArray.html.
APA
Wolfram Language. (2003). SparseArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SparseArray.html
BibTeX
@misc{reference.wolfram_2025_sparsearray, author="Wolfram Research", title="{SparseArray}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/SparseArray.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_sparsearray, organization={Wolfram Research}, title={SparseArray}, year={2021}, url={https://reference.wolfram.com/language/ref/SparseArray.html}, note=[Accessed: 17-February-2026]}