VarianceEquivalenceTest

VarianceEquivalenceTest[{data1,data2,…}]

dataiの分散が等しいかどうかの検定を行う．

VarianceEquivalenceTest[{data1,…},"property"]

"property"の値を返す．

詳細とオプション

  • VarianceEquivalenceTestは，真の母分散が同一である( 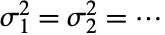)という帰無仮説 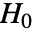と少なくとも1つの分散が異なるという対立仮説 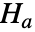で dataiについて仮説検定を行う．
  • デフォルトで，確率値すなわち 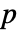値が返される．
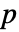  • 値が小さい場合は 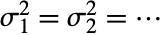である可能性が低いことを示唆する．
  • data は一変量{x1,x2,…}でなければならない．
  • VarianceEquivalenceTest[{data1,…}]はデータに適用可能で最も強力な検定を選ぶ．
  • VarianceEquivalenceTest[{data1,…},All]はデータに適用可能な検定をすべて選ぶ．
  • VarianceEquivalenceTest[{data1,…},"test"]は"test"に従って 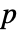値をレポートする．
  • ほとんどの検定は正規分布に従う dataiを必要とする．検定が正規性の仮定についてそれほど敏感ではない場合，その検定は強力であると呼ばれる．検定の中には datai が中央値に対して対称であると仮定するものもある．
  • 使用可能な検定
  • "Bartlett"正規性修正尤度比検定
    "BrownForsythe"頑健性頑健なLevene検定
    "Conover"対称性Conoverの二乗順位’検定
    "FisherRatio"正規性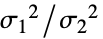に基づく
    "Levene"頑健性,対称性個々の分散とグループの分散を比較する
  • VarianceEquivalenceTest[{data1,…},"HypothesisTestData"]は htd["property"]の形で追加的な検定結果と特性の抽出に利用できるHypothesisTestDataオブジェクト htd を返す．
  • VarianceEquivalenceTest[{data1,…},"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "AllTests"適用可能なすべての検定のリスト
    "AutomaticTest"Automaticが使われた場合に選ばれる検定
    "DegreesOfFreedom"検定で使われる自由度
    "PValue" 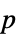値のリスト
    "PValueTable" 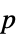値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 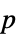値のペアのリスト
    "TestDataTable" 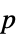値と検定統計のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 使用可能なオプション
  • SignificanceLevel 0.05診断とレポートのための切捨て
    VerifyTestAssumptions Automaticどの診断検定を実行するかを決める
  • 分散検定では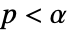， のときにのみ 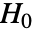が棄却されるような切捨て 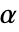が選ばれる．"TestConclusion"および"ShortTestConclusion"特性に使われる 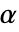の値はSignificanceLevelオプションで制御される．値 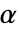は正規性と対称性の検定を含む仮定の診断検定にも使われる．デフォルトで 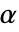は0.05である．
  • VarianceEquivalenceTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Normality"すべてのデータが正規分布に従っていることを証明する
    "Symmetry"すべてのデータが対称であることを証明する

例題

すべて開くすべて閉じる

例  (2)

等価性について，2つのデータ集合から分散を検定する：

さらに特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

完全な検定表：

複数のデータ集合の分散を同時に比較する：

データ集合の分散：

スコープ  (12)

検定  (8)

2つのデータ集合の分散を比べる：

分散が等しい場合は， 値は通常大きい：

分散が等しくない場合は， 値は通常小さい：

Automaticを使うと，一般に最も強力で適切な検定が適用される：

特性"AutomaticTest"は，どの検定が選ばれたのかを調べるのに使える：

数多くのデータ集合の分散を同時に比べる：

SmoothHistogramを使って視覚的にデータ集合の分布を比べる：

等分散について特定の検定を行う：

任意数の検定を同時に行うことができる：

データに適切な検定をすべて同時に行う：

特性"AllTests"を使ってどの検定が使われたのかを調べる：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

HypothesisTestDataオブジェクトから特性をいくつか抽出する：

ルベーン(Levene)検定からの 値と検定統計：

任意数の特性を同時に抽出する：

Brown–Forsythe検定からの 値と検定統計：

レポート  (4)

いくつかの検定からの結果を表にする：

適切な検定結果すべての完全な表：

選択された検定結果の表：

カスタマイズしたレポート用に検定表から項目を取り出す：

値が0.05より大きいので，このレベルでは正規性を退けるのに十分な証拠はない：

検定あるいは検定グループの 値を表にする：

表の 値：

すべての適切な検定の 値の表：

検定の一部からの 値の表：

検定あるいは検定グループからの検定統計をレポートする：

表からの検定統計：

すべての適切な検定からの検定統計の表：

オプション  (6)

SignificanceLevel  (3)

診断検定の有意水準を設定する：

デフォルトで0.05が使われる：

有意水準を設定することによって自動的にどの検定が選ばれるかが変わることがある：

順位に基づく検定がデフォルトでは選ばれたはずである：

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

VerifyTestAssumptions  (3)

診断は，AllかNoneを使ってまとめて制御することができる：

すべての仮定を検証する：

どの仮定もチェックしない：

診断は個々に制御することができる：

正規性を仮定するが，対称性についてチェックする：

正規性についてのみチェックする：

検定の仮定値は明示的に指定できる：

データが正規分布に従っていなかったため，上記ではConover検定が選ばれた：

アプリケーション  (2)

母集団群が共通の分散を持つかどうかについての検定を行う：

最初のデータ集合群は全く異なる分散を持つ母集団から引き出された：

2つ目の群からの母集団はどれも似た分散を持つ：

LocationEquivalenceTestを使っていくつかのデータ集合の平均を同時に比べることができるが，データ集合は共通の分散を持っていなければならない：

VarianceEquivalenceTestを使って分散が等しいかどうかを調べる：

LocationEquivalenceTestを使って平均を比べることができる：

特性と関係  (5)

Brown–Forsythe検定とルベーン(Levene)検定は等しいが，異なる標準化関数を使う：

ルベーン検定はMeanを使ってデータを標準化する：

Brown–Forsythe検定は通常Medianを使う：

裾部の重いデータについては，10%のTrimmedMeanが代りに使われる：

個のデータ集合と 個の合計観察について，Brown–Forsythe検定とルベーン検定はどちらも においてFRatioDistribution[k-1,n-k]に従う：

Bartlettの検定統計：

において検定統計はChiSquareDistribution[k-1]に従う：

分散の等価性検定は，入力がTimeSeriesのときはタイムスタンプを無視する：

分散の等価性検定は，TemporalDataの経路構造を認識する：

この値を直接使う：

考えられる問題  (2)

フィッシャー(Fisher)の比率検定は2つのデータ集合を必要とする：

他の検定のいずれかを代りに使う：

Conover検定だけは，データが正規分布に従うことを仮定しない：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), VarianceEquivalenceTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

テキスト

Wolfram Research (2010), VarianceEquivalenceTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

CMS

Wolfram Language. 2010. "VarianceEquivalenceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

APA

Wolfram Language. (2010). VarianceEquivalenceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html

BibTeX

@misc{reference.wolfram_2024_varianceequivalencetest, author="Wolfram Research", title="{VarianceEquivalenceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_varianceequivalencetest, organization={Wolfram Research}, title={VarianceEquivalenceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html}, note=[Accessed: 21-November-2024 ]}