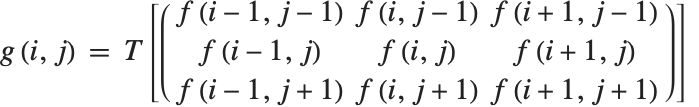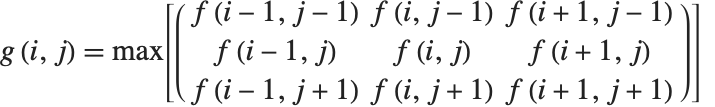画像処理
Wolfram言語は,プログラム的でもありインタラクティブでもある画像処理機能の組込みサポートを提供するようになった.これは,Wolfram言語のパワフルな数学的またアルゴリズム的機能と完全に統合されている.画像を作成してインポートしたり,組込み関数でそれを操作したり,線形および非線形フィルタを適用したり,さまざまな方法で可視化したりすることができる.
画像は数値配列から作成することもできるし,カットアンドペーストでWolfram言語のグラフィックスから,またImportを使って外部のソースからでも作成することができる
| Image[data] | data で与えられる画素値を持つラスター画像 |
| Import["file"] | ファイルからデータをインポートする |
| CurrentImage[] | カメラやその他のデバイスからの画像をキャプチャする |
画像オブジェクトを作成する一番簡単な方法は,0から1までの実数値の行列をImageでラップすることである.
また,他のアプリケーションから画像をコピーアンドペーストしたりドラッグアンドドロップしたりすることもできる.Importを使うと,ローカルのファイルシステムにあるファイルやアクセス可能なリモートの場所にあるファイルの画像を得ることができる.
次はWolfram言語のドキュメントディレクトリExampleDataから画像をインポートする:
| ImageDimensions[image] | image に関連するラスターの画素次元を返す |
| ImageAspectRatio[image] | image の縦横比を与える |
| ImageChannels[image] | image のデータにあるチャンネルの数を与える |
| ImageColorSpace[image] | image の色空間の名前を与える |
| ImageType[image] | image 中の各画素要素に使われている値のもとになっているタイプを返す |
| ImageQ[image] | |
| Options[symbol] | シンボルに割り当てられたデフォルトオプションのリストを与える |
| ImageData[image] | image の画素値の配列を与える |
画像の画素値の配列は関数ImageDataを使って簡単に抽出することができる.デフォルトでは,この関数は実数値を返すがオプショナルの「type」引数を使うと特定のタイプを指定することができる.
マルチチャンネルの画像の場合,2つの方法のうちオプションInterleavingで指定された配列方法で,生の画素データが3D配列として表される.
デフォルト設定のInterleaving->Trueでは,データはカラー値のリストの2D配列としてまとめられる.これはRGB色空間の画像で一般的な3つ1組の形式である.
オプション設定Interleaving->Falseは,1つのカラーチャンネルにつき1つの行列のリストとして,生のデータを保存したり取り出したりするのに使うことができる.
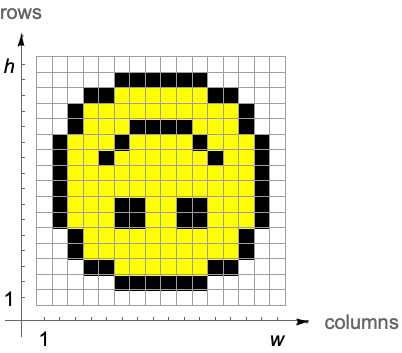
画像処理コマンドの中には,画像領域の位置を必要としたり,それを返したりするものがある.画素の位置を指定するためには,座標系が必要である.使用される座標系は複数あることに注意する.ここではインデックス座標と画像座標を区別する.
インデックス座標
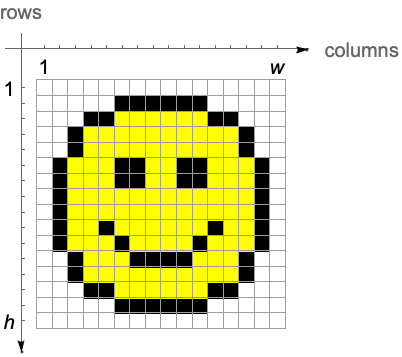
Imageは配列の行を上から下へと描画する:
画像と配列の両方に作用するWolfram言語コマンドは,インデックス座標系に忠実である.これらのコマンドはまず垂直の行座標を参照するパラメータをリストし,次に水平の列座標を参照するパラメータをリストする.
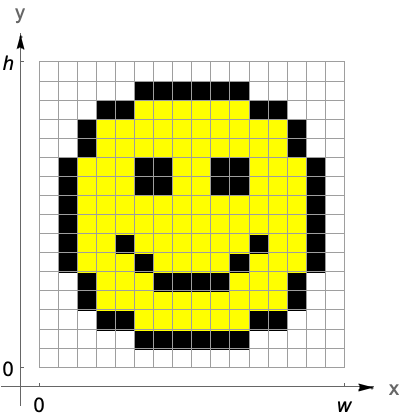
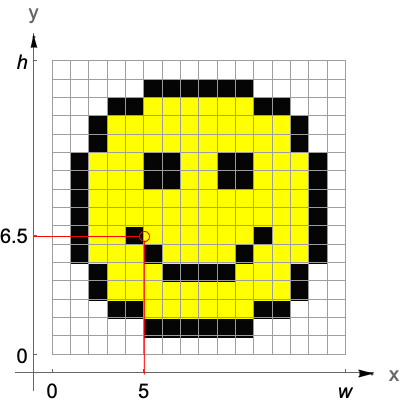
画像座標
2つ目の座標系は,データに備わっているものではなく埋込み空間に付随するものである.グラフィックス座標系のように,連続画像座標系には画像の左下に原点があり,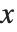 座標は左から右に,
座標は左から右に,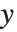 座標は上向きに伸びる.画像領域は二次元区間
座標は上向きに伸びる.画像領域は二次元区間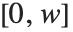 ×
×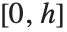 をカバーする.
をカバーする.
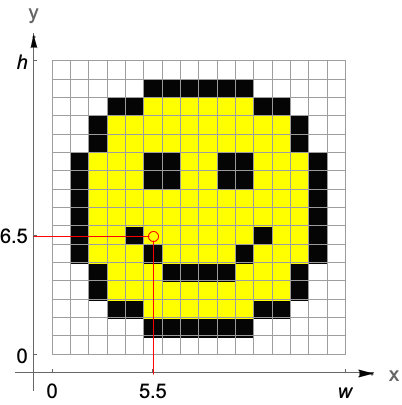
画像の画素は連続する整数座標値の間に区間でカバーされる.したがって非整数の座標は一義的に単独の画素を参照する.しかし,画素の境界に位置する整数座標は,隣接するすべての画素を考慮に入れ,それらすべての画素を選ぶかその平均の色の値を取るかする.
任意の配列に適用できない画像処理コマンドは,標準的な画像座標で結果を描画する.このような標準的な画像座標はGraphicsプリミティブで使うことができる.
ImageLinesは標準的な画像座標で線を返す:
| PixelValue[image,{x,y}] | 位置{x,y}における画像の画素値を与える |
| PixelValuePositions[image,val] | 値 val にマッチする image 内の画素の位置のリストを返す |
| ReplacePixelValue[image,{xp,yp}->val] | image 内の画素の位置{xp,yp}における画素値を val に変更する |
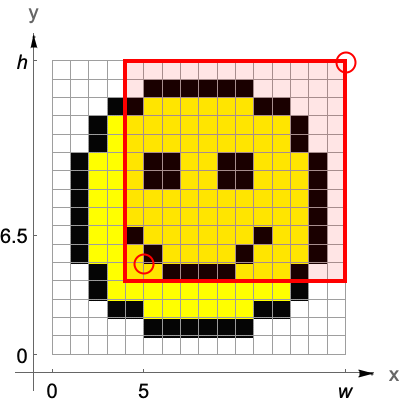
切取りや充填により画像次元を変更する画像操作を考えてみる.切取りを使うと,大きい画像の選択した部分から新しい画像を作成することができる.また,充填は通常,多数の画像処理タスクにおいて境界の画素が確実に一様に扱われるよう,境界で画像を拡張するために使われる.
| ImageTake[image,n] | image の最初の n 行からなる画像を返す |
| ImageCrop[image] | 同一色の境界を取り除くことで image を切り取る |
| ImageTrim[image,{{x1,y1},…}] | 指定された{xi,yi}画素が含まれるように image をトリミングする |
| ImagePad[image,m] | image の四方をそれぞれ m 個の背景画素で充填する |
ImageCropはImageTakeを補うものである.抽出する行数や列数を厳密に指定する代りに,結果の画像における所望の次元,つまり取り出される行数・列数を定義することができる.デフォルトではトリミングは中心を基準としているので,画像の両端から同数の行および列が削除される.
ImageCropは主にソース画像の次元を減らすために使われるが,その次元を増すために画像を充填しておいた方がよいことがよくある.非常に一般的な充填方法はすべてサポートされている.
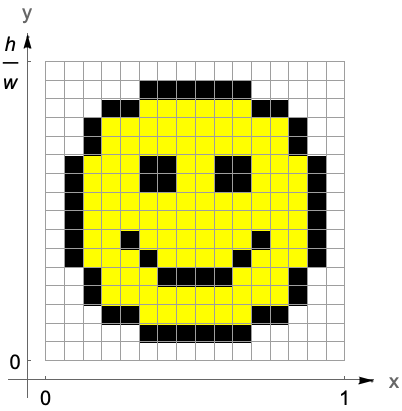
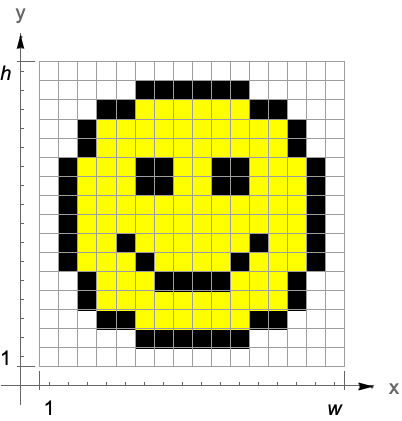
| ImageResize[image,w] | w 画素幅にリサイズされた image を返す |
| Thumbnail[image] | image のサムネイル版を与える |
| ImageRotate[image] | image を反時計回りに90°回転させる |
| ImageReflect[image] | 上下が鏡映に正反射になるように imageを反転させる. |
次ではもとの画像の大きさを増加させるため,また減少させるためにImageResizeが使われている:
ImageRotateもよく使われる空間操作である.これを使うと,画素位置が画像の回転軸を中心として反時計回り回転した画像が返される.
便利な画像処理でも,2つの画像間,または1つの画像と1つの定数間の簡単な演算操作だけしか必要ないものもある.例えば,明度は,画像に定数係数を掛けるか,画像に定数を足す(あるいは画像から定数を引く)ことにより変更することができる.さらに,2つの画像の差分を使って変更を検出することもできれば,2つの画像の積を使ってマスキングという操作において画像の部分を隠したりハイライトしたりすることもできる.このような目的で,3つの基本的演算関数が利用できる.
| ImageAdd[image,x] | image 中の各チャンネルに x を加える |
| ImageSubtract[image,x] | 一定量 x を image 中の各チャンネル値から減算する |
| ImageMultiply[image,x] | image 中の各チャンネル値に因子 x を掛ける |
点操作は簡単ではあるが重要な画像処理のクラスとなっている.これらの操作は画像の輝度値を変更するため,画像が表示されたときにどのように見えるかを修正する.この言葉は点操作が入力として単一画素を取るということがもととなっている.これは以下の式
で表すことができる.ここで 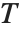 は入力画像
は入力画像 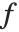 と結果
と結果 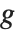 の間のマッピングを指定するグレースケール変換を,
の間のマッピングを指定するグレースケール変換を,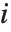 ,
, 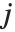 はそれぞれ画素の行および列の指標を表す.点演算は,変換 T を定義するある関数に従った,もとの(入力)画像と修正された(出力)画像との間の1対1のマッピングである.
はそれぞれ画素の行および列の指標を表す.点演算は,変換 T を定義するある関数に従った,もとの(入力)画像と修正された(出力)画像との間の1対1のマッピングである.
コントラストの変更
| Lighter[image,
…
] | image の色を明るくしたものを表す |
| Darker[image,
…
] | image の色をより暗くした色を表す |
| ColorNegate[image] | すべての色が無効になった image のネガを返す |
| ImageAdjust[image] | 0から1の範囲をカバーするように image 内のレベルを調節する |
| ImageApply[f,image] | image 中の各画素チャンネル値のリストに関数 f を適用する |
画像二値化は多値画像を二値画像に変換する操作を言う.二値画像では,各画素値は1つの二進数の桁で表される.この最も単純な形式である二値化(閾値指定ともいう)は,ある大域的閾値 t との比較に基づいて画像の各画素に値0か1を割り当てる点ベースの操作である.
二値化ではデータ保存の量が格段に減り,解析がより簡単な二値画像になるという理由で,初期の処理プロセスで便利なものである.二値画像では,形状に対してパワフルな形態演算子を使ったり画像内容の構造ベースの解析を使ったりすることができる.二値化は画像を別々の領域へと分割するので,画像分割の形式でもある.
| Binarize[image] | image からバイナリ画像を作成する |
| ColorQuantize[image,n] | 異なる色を n 色しか使わないように image を近似する |
ここでImageApplyは,各チャンネルが二値化されるカラー画像を返すために使われている.その結果は最大8色になる:
色変換
RGBカラースキームは,最もよく使用されている色表現である.いわゆる三原色がさまざまな割合で混ざり(加わり),複合された完全色の画像が生成される.RGBカラーモデルはカラーモニタ,ビデオレコーダ,カメラで世界的に使われている.また,人間の視覚はこれらの原色のいろいろな組合せとして色を感知するようになっている.同量ずつ加えられた原色は,光の等和色であるシアン(C),マゼンタ(M),黄(Y)を生成する.これらは印刷業界で使用されている色の原色であり,つまりCMYカラーモデルに関連するのである.画像処理アプリケーションでは,色の情報を輝度から分けた方が便利なことがよくある.HSB(色調,彩度,明度)モデルにはこの特性がある.色調は観察者によって見られるようなドミナントカラーを,彩度は色の白光との希釈量を,明度は平均輝度を定義する.したがって,輝度の要素は画像の色情報とは独立して処理される.
| ColorConvert[expr, colspace] | expr の色情報を変換し,colspace により表される色空間を表す |
画像ヒストグラム
多くの画質改善操作に共通の重要な考え方に,ヒストグラムの概念がある.これは単に画像のグレーレベルの数(正規化されていれば相対頻度)である.ヒストグラムの解析は画像のコントラストについての便利な情報を与えてくれる.画像のヒストグラムは多くの画像処理の分野(特に圧縮,分割,閾値割当て)で重要である.
| ImageLevels[image] | image の各チャンネルの画素値と画素数のリストを返す |
| ImageHistogram[image] | image 中の各チャンネルについて画素レベルのヒストグラムをプロットする |
画像処理操作で最も便利なのが領域ベースのものである.領域ベースの操作は局所的な,通常小さい近傍の値に基づいて新しい画素値を計算する.これは通常定サイズ演算子(フィルタ)を使った線形あるいは非線形のフィルタ操作で実装される.一般性を失うことなく,位置が 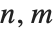 で値が
で値が 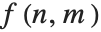 の画像画素の中心からの対称3 × 3近傍を考えてみる.一般的な領域ベースの変換は以下のように表すことができる.
の画像画素の中心からの対称3 × 3近傍を考えてみる.一般的な領域ベースの変換は以下のように表すことができる.
ここで 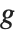 は変換
は変換 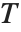 を入力画像
を入力画像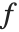 のすべての画素に対する中心から3×3の近傍に適用することで得られた出力画像である.近傍の空間次元と空間幾何は通常応用分野の必要性に応じて決定される.画像処理の領域ベースの操作には,ノイズの軽減,エッジ検出,エッジ強調,画像改善,分割がある.
のすべての画素に対する中心から3×3の近傍に適用することで得られた出力画像である.近傍の空間次元と空間幾何は通常応用分野の必要性に応じて決定される.画像処理の領域ベースの操作には,ノイズの軽減,エッジ検出,エッジ強調,画像改善,分割がある.
線形および非線形フィルタ
たたみ込みを使った線形画像フィルタは,画像処理で最も広く使われるメソッドのひとつである.所望の結果を得るためには,適切なフィルタを指定する必要がある.平滑化,強調,エッジ検出,ズームはたたみ込みベースの実装を伴う画像処理タスクの例である.例題のノイズ削除等,このほかのタスクは非線形処理を使った方がうまく行く.
| ImageFilter[f,image,r] | 関数 f を image の各チャンネル内の各画素の範囲 r の近傍の適用する |
| ImageConvolve[image,ker] | 核 ker による image のたたみ込みを与える |
通常の線形フィルタが使えず,所望の操作が組込みフィルタ関数のいずれによっても実装されない場合は,より一般的ではあるが遅いImageFilter関数を使うことができる.
| Blur[image] | image のぼやけたものを与える |
| Sharpen[image] | image をよりシャープにして返す |
| MeanFilter[image,r] | 範囲 r ですべての値を平均値で置換する |
| GaussianFilter[image,r] | 画素半径 r のガウシアン(Gaussian)カーネルでたたみ込む |
| MedianFilter[image,r] | 範囲 r のすべての値を中央値で置換する |
| MinFilter[image,r] | 各値を範囲 r における最小値で置換する |
| CommonestFilter[image,r] | 各画素を範囲 r の近傍中の最も一般的な画素値で置換する |
画像処理においてより一般的に線形フィルタが適用される例として,離散導関数の近似とそれに続くエッジ検出の計算がある.よく知られているPrewitt,Sobel,Cannyの方法は,本質的に画像の各点における2つの直交した微分および勾配の大きさの計算に基づいている.
2つ目の例として,画像からインパルス性ノイズ(外見からゴマ塩雑音とも呼ばれる)を除去するタスクを考えてみる.これは線形の移動平均値と非線形走査中央値から生成される異なる結果を比較する典型的な例である.
形態学的処理
数理形態学は,ある場面のオブジェクトの空間的構造に基づいたデジタル画像を処理するアプローチを提供する.二値形態学では,これまで説明した線形・非線形の演算子と異なり,形態的演算子は画素集合の大きさではなく形状を修正する.しかしこれらの演算子と類似して,二値形態的演算子は基本的な加算および乗算演算子を論理記号のORおよびANDで置き換えたたたみ込みのようなアルゴリズムを使って実装されることがある.
二値形態学の定義は,ブール代数のANDおよびORがそれぞれ点についての最小演算子および最大演算子になったグレースケール画像の領域にまで自然に拡大される.一様な零値の構造要素では,画像 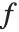 の膨張は次の簡単な形式に還元される.
の膨張は次の簡単な形式に還元される.
これらの演算子は単独の構造要素あるいはそのような要素のリストを使った組合せで使用することができ,多くの便利な画像処理タスクを実行する.その例として,細線化,太線化,エッジおよびコーナー検出,背景正規化がある.
| GeodesicDilation[marker,mask] | 画像 mask によって制約された画像 marker の測地的な膨張の固定点を与える |
| GeodesicErosion[marker,mask] | 画像 mask で制約されている画像 marker の測地的収縮の固定点を与える |
| DistanceTransform[image] | image の距離変換を行う.この変換で,各画素の値は直近の背景画素までの距離で置換される |
| MorphologicalComponents[image] | image 中の各画素が,その画素がある接続された前面の画像要素を表す整数指数で置換された配列を与える |
形態学的再構成とも呼ばれる,形態学的アルゴリズムの重要なカテゴリは,マーカー画像に繰返し適用される膨張(収縮)に基づく一方,それぞれのステップの結果は2つ目の画像であるマスクにより制約される.この処理は固定点に達したところで終了する.面白いことに,画像処理タスクの多くには,再構成という点で自然な方式を持っている.山および谷の検出,穴埋め,領域のフラッド,ヒステリシス閾値等が例として挙げられる.二重閾値とも言われるヒステリシス閾値は,広く使用されるCannyエッジ検出の中心的部分である.低閾値を下回る画素は拒否され,高閾値を上回る画素が受け入れられる一方,中間範囲の画素は高閾値の画素に接続している場合のみ受け入れられる.接続性はさまざまなアルゴリズムを使って構築できるが,再構成により効率的で簡単なソリューションが与えられる.