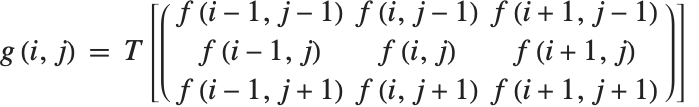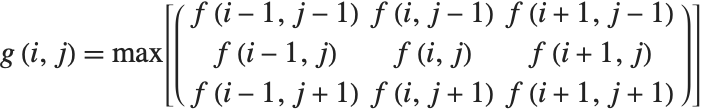图像处理
Wolfram 语言对编程式的和交互式图像处理都提供内置的支持,和 Wolfram 语言强大的数学和算法功能完全地结合在一起. 你能创建和导入图像,用内置函数对它们进行操作,应用线性的和非线性的滤波器,以及用几种不同的方式来显现它们.
图像可以通过数值数组,通过对 Wolfram 语言图形剪贴的方法,以及通过用 Import 从外部来源来创建.
| Image[data] | 像素值由 data 给出的光栅图像 |
| Import["file"] | 从一个文件导入的数据 |
| CurrentImage[] | 从摄像头或者其他设备捕捉图像 |
创建一个图像对象的最简单的方法是用 Image 封装一个从0到1的实数矩阵.
另一个方法是从某些其它的应用程序中复制和粘贴或拖放一个图像. 你可以用 Import 从一个当地文件系统中或任何可进入的远程文件中获得一个图像.
这里从 Wolfram 语言的文件目录 ExampleData 中输入一个图像:
| ImageDimensions[image] | 给出和 image 相联系的光栅的像素尺寸 |
| ImageAspectRatio[image] | 给出 image 高宽比例 |
| ImageChannels[image] | 给出在 image 数据中存在的通道的数目 |
| ImageColorSpace[image] | 给出与 image 相关的色彩空间 |
| ImageType[image] | 给出 image 中的每一个像素元素所用的数值类型 |
| ImageQ[image] | |
| Options[symbol] | 给出赋予一个符号的默认选项的一个列表 |
| ImageData[image] | image 中像素值阵列 |
在多通道图像的情况下,原始的像素数据是用一个三维数组来表示的,它按照由 Interleaving 选项决定的两种可能方法之一来排列.
在默认的 Interleaving->True 设置下,数据被组织成一个颜色值列表的二维数组,颜色值列表在 RGB 颜色空间图像的普通情况下由三个数组成.
Interleaving->False 这个选项设置能用来把原始数据作为矩阵的列表来存储和提取,每一个矩阵对应一个颜色通道.
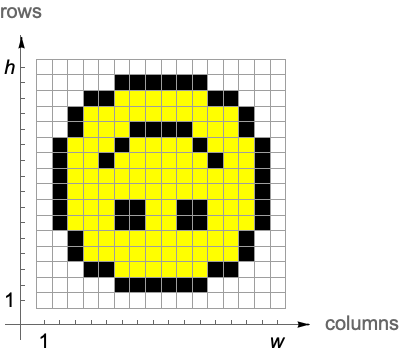
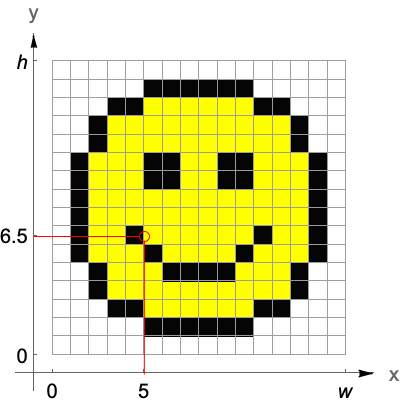
索引坐标
Image 对数组各行从上到下进行渲染:
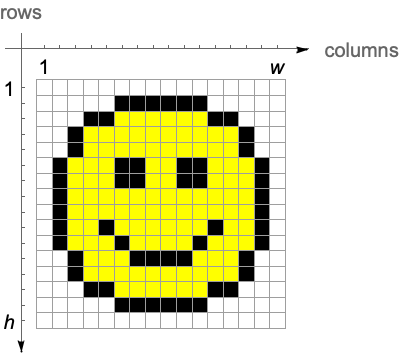
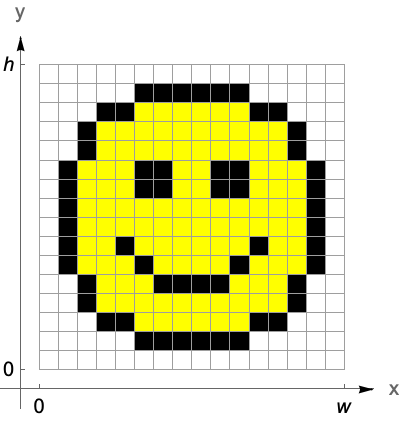
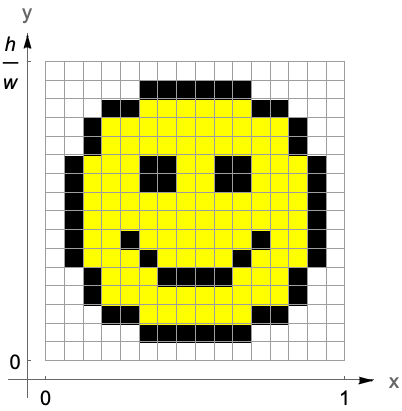
图像坐标
适用于任意阵列的图像处理命令,将在标准图像坐标中对结果进行渲染. 这些标准图像坐标可以很容易地在 Graphics 的基元中使用.
ImageLines 返回标准图像坐标中的线条:
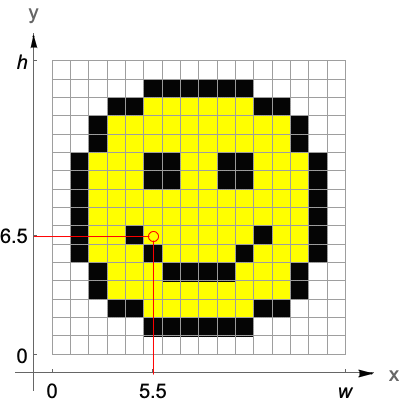
| PixelValue[image,{x,y}] | 给出图像在位置 {x,y} 处的像素值 |
| PixelValuePositions[image,val] | 返回 image 中与值 val 匹配的像素位置列表 |
| ReplacePixelValue[image,{xp,yp}->val] | 将 image 中位置 {xp,yp} 处的像素值变更为 val |
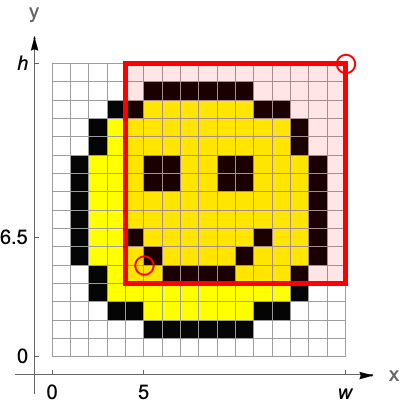
考虑通过剪切或填充来改变图像尺寸的图像操作. 这些操作有各种不同的用处. 剪切允许你从一个大的图像中选择一部分来创建出一个新的图像,而在图像处理中,填充通常是用来在边沿上延伸图像以确保边沿像素的均匀处理.
| ImageTake[image,n] | 给出一个由 image 的前 n 行组成的图像 |
| ImageCrop[image] | 通过去除颜色均匀的边沿来剪切 image |
| ImageTrim[image,{{x1,y1},…}] | 对 image 进行裁剪以囊括指定的 {xi,yi} 像素 |
| ImagePad[image,m] | 用 m 个背景像素来填充 image 的所有边沿 |
ImageCrop (图像剪切)方便地补充了 ImageTake. 它不是指定要被提取的确切的行数和列数,相反的,它允许你定义新产生的图像的理想尺寸,也就是,要保留的行数和列数. 默认下,剪切操作是中心进行的,即从图像的边缘上删除相同数量的行和列.
ImageCrop 主要是用来减小源图像的尺寸,人们也常常希望填充一个图像使得它的尺寸增加. 这里支持所有最普遍的填充方法.
| ImageResize[image,w] | 给出一个 w 像素宽,重新改变了尺寸的 image 版本 |
| Thumbnail[image] | 给出 image 的一个缩略图 |
| ImageRotate[image] | 逆时针旋转 image 90° |
| ImageReflect[image] | 用上下镜面反射翻转 image |
这里, ImageResize 用来增加和缩减原始图像的大小:
ImageRotate 是另一个常用的空间操作. 它产生的图像,其所有像素都相对于图像中心的支点有一个逆时针旋转.
有一些有用的图像处理任务只要求在两个图像或一个图像和一个常数之间进行简单的算术运算. 例如,你能通过将一个图像和一个常数因子相乘或往(从)一个图像中加(减)一个常数来改变明度. 更有趣的是,两个图像之间的差别能够用来发现变化,两个图像之间的乘积能用来隐藏或突出一个图像的某些区域,这个过程叫做掩模(masking). 对于这个用途,有三个基本的算术函数可用.
| ImageAdd[image,x] | 给 image 中的每一个通道值加上一个量 x |
| ImageSubtract[image,x] | 从 image 中的每一个通道值中减去一个常数量 x |
| ImageMultiply[image,x] | 将 image 中的每一个通道值和一个因子 x 相乘 |
对比度修改
| Lighter[image,
…
] | 给出 image 的一个亮一点版本 |
| Darker[image,
…
] | 给出 image 的一个暗一点版本 |
| ColorNegate[image] | 给出 image 的负本,在其中所有的颜色都被求反了 |
| ImageAdjust[image] | 调整 image 中的级别,使它们按比例调节到0到1的范围里 |
| ImageApply[f,image] | 把 f 应用于 image 中每一像素的通道值列表 |
图像二值化是一个把多级的图象转换成一个二值图像的操作. 在一个二元图像中,每一个像素的数值由一个单一的二进制数字代表. 在它最简单的形式下,二值化,也叫做阈值化,是一个基于点的操作,它根据和某一个总体的阈值 t 相比较来给一个图像的每一个像素赋予一个0或1的值.
阈值化是一个引人注目的早期处理步骤,因为它导致数据存储量上极大的减小并且产生更易于分析的二值图像. 二值图像允许使用强大的形态运算符来对图像内容进行基于形状和结构的分析. 二值化也是图像分割的一种形式,因为它把一个图像分割成不同的区域.
| Binarize[image] | 从 image 创建一个二值图像 |
| ColorQuantize[image,n] | 给出仅用 n 个不同颜色的近似 image |
这里 ImageApply 用来返回一个彩色图像,在其中每一个单独的通道都被二值化了,导致最多8个不同的颜色:
颜色转换
在实际使用中,RGB (红色、绿色、蓝色)颜色配合是最常用的颜色表达方式. 这三个所谓的主色彩用不同的比例合并在一起(加在一起)来产生一个复合的,全色彩的图像. RGB 颜色模式在彩色监视器,录像机和照相机里普遍使用. 而且,人的视觉系统也是通过把颜色调节成这些主色彩的不同组合来感知的. 相同数量的主色彩加在一起产生光的次要色彩:青绿色 (C),品红色(M),和黄色(Y). 这是用于印刷业中的主要色素颜色,所以显示出 CMY 颜色模式的重要性. 对图像处理的应用,把颜色信息从明视度上分开出来经常是有用的. HSB(色相、饱和度、明度)模式有这个特性. 色相代表观察者所看见的主要颜色,饱和度指的是用白光对颜色的稀释量,明度定义平均的亮度. 亮度这一成分,因此,可以独立于图像颜色信息来处理.
| ColorConvert[expr, colspace] | 把 expr 里的颜色指定转换成由 colspace 代表的颜色空间 |
图像直方图
普遍地对于很多图像增强操作的一个重要概念是直方图,它只是一个对图像中灰色级别的一个计数(或相对频率,如果是归一化的). 对直方图的分析给出关于图像对比的有用信息. 图像直方图在图像处理的很多领域中都很重要,最显著的是压缩、分割和阈值.
| ImageLevels[image] | 对 image 中的每一个频道给出一列像素数值和计数 |
| ImageHistogram[image] | 对 image 中的每一个频道画出一个像素级别的直方图 |
大多数有用的图像处理算符都是基于区域的. 基于区域的操作根据在一个局部的,通常小的邻近区域中的数值来计算一个新的像素数值. 这一般是通过用一个有限大小的算符(比如,一个滤波器)进行的线性或非线性的滤波操作来履行的. 不失去一般性,考虑一个位于 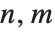 ,数值为
,数值为 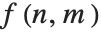 的图像像素中心的一个对称的 3×3 的邻近区域. 一个普遍的基于区域的变换能被表示为
的图像像素中心的一个对称的 3×3 的邻近区域. 一个普遍的基于区域的变换能被表示为
这里 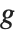 是由把
是由把 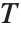 变换应用到输入图像
变换应用到输入图像 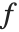 中所有像素位于中心的 3×3 邻域而产生的输出图像. 应该注意到邻域的空间尺寸和几何形状一般是由应用的需要而决定的. 基于区域的图像处理操作的例子包括降低噪声,边缘检测,边缘锐化,图像增强和分割.
中所有像素位于中心的 3×3 邻域而产生的输出图像. 应该注意到邻域的空间尺寸和几何形状一般是由应用的需要而决定的. 基于区域的图像处理操作的例子包括降低噪声,边缘检测,边缘锐化,图像增强和分割.
线性和非线性滤波
使用卷积的线性图像滤波是处理图像的最通用的方法之一. 为了达到一个理想的结果,你必须指定一个合适的滤波器. 例如平滑,锐化,边缘检测,以及变焦这样的任务都是典型的基于卷积来实施的图像处理任务的例子. 其它的任务,例如噪声去除,最好是用非线性的处理技术来完成.
| ImageFilter[f,image,r] | 把 f 应用于 image 的每一个通道中的每一个像素的 r 范围 |
| ImageConvolve[image,ker] | 给出 image 和内核 ker 的卷积 |
更普遍的(但速度上会慢一些的)ImageFilter 函数能在传统的线性滤波不能用,并且理想的操作不能由任何固定的滤波函数来履行的情况下使用.
| Blur[image] | 给出一个模糊的 image 版本 |
| Sharpen[image] | 给出一个锐化的 image 版本 |
| MeanFilter[image,r] | 对每一个数值用它的范围 r 的平均值替换 |
| GaussianFilter[image,r] | 同一个像素半径为 r 的 Gaussian 内核卷积 |
| MedianFilter[image,r] | 对每一个数值用它的范围 r 的中位数替换 |
| MinFilter[image,r] | 对每一个数值用它的范围 r 的最小值替换 |
| CommonestFilter[image,r] | 对每一个像素用它的范围 r 中最普遍的像素值替换 |
在图像处理中更普遍的线性滤波的应用之一是对离散导数的近似计算,因而边缘检测. 众所周知的 Prewitt、Sobel 和Canny 的方法本质上都是基于对图像中每一点的两个正交的导数和梯度大小的计算上的.
形态处理
数学形态提供了一个处理基于景色中物体的空间结构的数字图像的方法. 在二值形态中,和目前为止讨论的线性和非线性算符不一样,形态算符改变像素群的形状而不是它们的振幅. 但是,和这些算符类似,二值形态算符可以用卷积一样的算法来履行,把基本的加法和乘法运算用逻辑的 OR(或)和 AND(与)来替换.
| GeodesicDilation[marker,mask] | 给出受图像 mask 约束的图像 marker 的短程膨胀的一个固定点 |
| GeodesicErosion[marker,mask] | 给出受图像 mask 约束的图像 marker 的短程腐蚀的一个固定点 |
| DistanceTransform[image] | 给出 image 的距离变换,在其中每一个像素的数值都被它到最近的一个背景像素的距离替代 |
| MorphologicalComponents[image] | 给出一个数组,在其中 image 的每一个像素都被代表那个像素所在的相联系的前景图像成分的整数指标所替代 |
一个重要的形态算法的种类,称为形态重新构造,是基于对一个标记图像反复地使用膨胀(或腐蚀),每一步的结果都受第二个图像,掩模的束缚. 这个过程在达到一个固定点时结束. 有趣的是,很多的图像处理的任务在重新构造方面都有一个自然的公式. 峰和谷的检测,洞的填充, 区域充斥,以及滞后阈值只是几个例子. 后者,也称为一个双阈值,是一个广泛被使用的 Canny 边缘检测器的不可缺少的一部分. 在低端阈值之下的像素被拒绝,在高端阈值之上的像素被接受,而在中间范围的像素只有在它们是和高阈值的像素“连接”时才会被接受. 连接可以用不同的算法来建立,但重新构造给出了一个有效而且非常简单的解决办法.