方程式と不等式の操作
| 方程式 | 変数の消去 |
| 方程式の解法 | 関係演算子と論理演算子 |
| 方程式と解の表現 | 論理結合した方程式の解法 |
| 一変数の方程式 | 不等式 |
| 多項式の根の数と分離 | 領域上の等式と不等式 |
| 代数的数 | 解の集合の表示 |
| 連立方程式 | 限定子 |
| 一般的な解と一般的ではない解 | 最小化と最大化 |
「変数の定義」において,x を y に等しくすることを表す x=y のような割当てについて述べた.ここでは,等号関係を判定するいわゆる方程式について説明していく.x が y に等しいかどうかを判定する方程式は,x==y と記述する.
ここで x=y と x==y の記述を混乱しないように注意してほしい.x=y は,命令的な表現であり,実際に割当てを実行するためにある.これに対して,x==y は,単に x と y が等しいかどうかを判定するだけのためにあり,それで何かが実行されるというようなことはない.C言語を使ったことのあるユーザなら,Wolfram言語で使われる割当て(assignment)と判定(testing)の操作がC言語のものと同じであることに気が付いたであろう.
記号で表された数式に対する判定でも,ケースによっては,確定した結果を得ることができる.ここで重要なケースとして,2つの同値の式に対して等号関係を判定することがある.これらの両方の式の変数がどんな数値であろうが,Wolfram言語は,式が常に等しいものと正確に解釈する.
Wolfram言語は,これらの式が等しいかどうかは判断しない.この場合は,Expandを使えば,同じ形にすることができる:
| Solve[lhs==rhs,x] | 方程式を解く(答は x への置換規則のリストとして出力する) |
| x/.solution | 答の置換規則を作用させ x 値のみをリスト出力する |
| expr/.solution | 答の置換規則を作用させ式の値をリスト出力する |
Solveを使うと,必ず方程式の解の明示的な式の導出が試みられる.しかし,数学の基本的な結果として判明しているように,式が十分に複雑ならば,根基による明示的な形の解を得ることは不可能である.変数が1つしかなく,最大でも次数が四次以下なら,Wolfram言語は必ずその解を式として求めることができる.しかし,五次以上の方程式では,すべての解を明示的な代数式として求めることは数学的に不可能である.
いくつかの方程式は,解は存在してもそれを明示的な式として表すことは不可能である.ここでは,Rootオブジェクトで解が表現される:
Solveを使い未知の関数を含んだ方程式を解くことも可能である.その場合も,警告が発せられるが,形式的な逆関数を使った結果を得ることができる.
| Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
変数 x, y, …について連立方程式を解く | |
一般に連立方程式が解を持つか持たないかは極めて微妙な問題である.例えば,連立方程式{x==1,x==a}において,aのほとんどの値に対して連立方程式は矛盾するため,xの解は存在しない.唯一,aが1に等しいときに,連立方程式は解を持つ.Solveは,方程式の一般解を求めるように設定されている,パラメータ間の特別な制約条件が満たされるときだけに存在する解は切り捨てられる.
| Solve[lhs==rhs,x] | x について方程式を解く |
| Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
x, y, …について連立方程式を解く | |
| Eliminate[{lhs1==rhs1,lhs2==rhs2,…},{x,…}] | |
連立方程式において x, …を消去する | |
| Reduce[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
連立方程式を変形・簡約し,条件付きであっても解を探す | |
Wolframシステムは方程式を論理構文として扱う.x^2+3x==2と方程式を入力すると,Wolframシステムはこれをx^2+3xは2に等しいとする構文として解釈する.xに特定の値を割り当てると(例えば,x=4というように),Wolframシステムが判断できるようになり,論理構文x^2+3x==2がFalseであることが判明する.
二次方程式x^2+3x==2は,xの値について暗示的な構文と考えられる.上の例で示したように,関数Reduceを使えば,より明示的にxの値を表した式に書き換えられる.Reduceが生成する式はx==r1x==r2の形を取る.この式もまた論理構文であり,「xは r1に等しい.あるいはxは r2に等しい」の意味を持つ.この論理構文を満たすxの値は,もとの二次方程式を満たすxの値と全く同じである.ただし,多くの場合,Reduceで得られる式の方がもとの方程式よりはるかに有用である.
方程式は他の論理構文と同じように組み合せたり,操作したりすることが可能である.や&&等の論理結合記号を使い,代替や連立の条件を設定できる.また,LogicalExpandやFullSimplifyのような関数を使い,方程式の組を簡約することも可能である.
方程式は,通常,論理構文として変形操作すると便利である.しかし,場合によっては,求められた方程式の解を他の計算に利用したい.そのような場合は,方程式を lhs==rhs のもとの形から lhsrhs の変換規則の形に置き換えておくとよい.解を変換規則の形にしておけば,置換記号/.を使い簡単に解を式に代入できるようになる.
ToRulesを作用させ,論理構文から変換規則のリストを作成する:
Solveを使うと,解が変換規則の形で生成される:
Solveやこれに関連したWolfram言語の関数は,主に整方程式(代数方程式)を扱う.
この例の式のように因数に分解する多項式なら,Solveを使うだけで簡単に根が見付かる:
この多項式は因数分解できないが,多項式の多項式という形をしているので,Solveで明示的な解を求めることができる.(今の例では,二次式の二次式の二次式という構造をしているので二次方程式を3回解くことになる.)
| Root[f,k] | 方程式 f[x]==0における k 番目の根を返す |
最終的に数値解がほしいのであれば,はじめからNSolveを使った方が速いことが多い:
これは上で論じた多項式の最初の根を表すRootオブジェクトである:
Roundは根に最も近い整数を求める厳密計算を行う:
方程式に存在する唯一の記号パラメータがそれについて解こうとしている変数の場合,方程式のすべての解はただの数になる.しかし,方程式にこの他のパラメータがあれば,一般に解はそれらのパラメータの関数になる.
Solveはこの方程式に2つの同一の解を与える:
方程式を何らかの多項式の形に簡約できる限り,Wolfram言語は常にその解をRootオブジェクトによって表現することができる.しかし,より一般的な,例えば超越関数を含む方程式の場合,Rootオブジェクトを使う系統立った方法はなく,数値近似を求める必要もない.
1変数の整方程式は有限個の解を持つ.しかし超越方程式はしばしば無限の解を持つことがある.関数が事実上無限の可能な逆方程式を持つから,というのがその理由である.しかし,デフォルトのオプション設定InverseFunctionsTrueだと,Solveはこのような関数には1つの逆関数があると仮定する.この場合,Solveはこの逆関数について特定の解を返すことができる場合がある.
Wolfram言語はProductLogについて特定の解を返し,併せて他の解が失われる可能性を示す警告メッセージを表示する:
| InverseFunction[f] | f の逆関数 |
| InverseFunction[f,k,n] | n 個の引数を持つ関数 f の k 番目の引数についての逆関数 |
Solveは式の特定の解しか返さないが,Reduceはすべての解のセットの表現を返すことができる.超越方程式の場合は例えば値の範囲がすべての可能な整数に及ぶような新たなパラメータを導入してしまうことがある.
「領域上の等式と不等式」で詳しく説明してあるように,Reduceを使うと変数の領域を制限することができる.これによって超越方程式の具体的な解を生成したり,あるいはそれが存在しないことを示したりできることがある.
Reduceを使うと解が存在しないことが分かる:
多項式の根を数える
| CountRoots[poly,x] | x の多項式 poly の実数根の数を返す |
| CountRoots[poly,{x,a,b}] |
CountRootsはガウス有理係数を持つ多項式を取る.根の数には多重根も含まれる.
分離区間
| RootIntervals[{poly1,poly2,…}] | polyi のいずれかの実数根に対する隣接しない分離区間のリストとともに,実際に各連続根を持つ多項式のリストを返す |
| RootIntervals[poly] | 単独の多項式の実数根に対する隣接しない分離区間を返す |
| RootIntervals[polys,Complexes] | polys の複素数根に対する隣接しない分離区間または矩形を返す |
| IsolatingInterval[a] | 代数的数 a に対して分離区間を返す |
| IsolatingInterval[a,dx] | 幅が最大で dx の分離区間を返す |
RootIntervalsは有理数係数の多項式を取る.
| Root[f,k] | 方程式 f[x]==0における k 番目の根を返す |
Rootの式を入力すると,その中に多項式があれば,式は自動的に最小な形に約される:
Wolfram言語では,代数的数,つまり有理数を係数とする代数方程式の根はRootを用いた式で表記される.代数的数は,ある代数演算を施したなら,演算結果は必ず単一の代数的数で得られる,という性質を持つ.
この例でも,単一なRoot式として根が求まる.ただし,かなり複雑になってしまう:
| RootReduce[expr] | 式 expr を単一なRoot式に約す |
| ToRadicals[expr] | Root式を明示的なベキ根に変換する |
簡単なRoot式なら,直ちにベキ根として表してくれる:
三次の多項式だと,Rootは自動的にはベキ根で表してくれない:
SolveやToRadicalsを使っても整方程式の解がベキ根の形で得られないなら,ほとんどの場合,そのような変形ははじめから数学的に無理だからである.ただし,式によっては基本的に可能だが,Wolframシステムで求められないときもある.そのような状況が 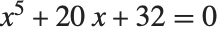 の式に当てはまるが,この方程式の解をベキ根で表すと非常に複雑になってしまう.
の式に当てはまるが,この方程式の解をベキ根で表すと非常に複雑になってしまう.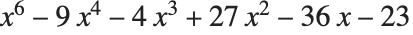 もそのような式の1つである.この場合には,
もそのような式の1つである.この場合には,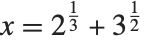 が1つの解である.
が1つの解である.
六次の多項式を持つRoot式が得られる:
ベキ根を使い簡単な形で表せるはずだが,ToRadicalsでは求まらない:
四次以上になると,ほとんどの多項式では,ベキ根で表せる根は存在しなくなる.一つ例外があり,それは式が五次の場合で,そのときは楕円関数や超幾何関数で表せることが知られている.それでも,得られる形が複雑過ぎて実際には使えない.
| RootApproximant[x] | 数 x を,それを最もよく近似する「最も簡単な」代数的数のひとつに変換する |
| RootApproximant[x,n] | x を近似する最大 n 次の代数的数を見付ける |
Nを適用し,数値近似的な解を得る:
何について解くのかSolveに指定しないと,方程式に含まれるすべての変数について解法が試される:
| ■ Solve[{lhs1==rhs1,lhs2==rhs2,…},vars] |
| ■ Solve[lhs1==rhs1&&lhs2==rhs2&&…,vars] |
| ■ Solve[{lhs1,lhs2,…}=={rhs1,rhs2,…},vars] |
Solveへの連立方程式の与え方
Solveはリストで表現された方程式を解のリスト,つまり等式のリストで返す:
LogicalExpandを使い,リストで表現された方程式を明示的な方程式のリストに変換できる:
計算の種類によっては明示的な式の代りに係数の配列を使うとよいことがある.そのような配列はCoefficientArraysを使って方程式から構築できる.
方程式が2x==0なら,唯一の可能な解がx0であることは明白である.しかし,方程式がax==0になると,話は少々複雑になる.aが0以外のとき,解はx0のみであるが,aが0のときは,xはどのような値でもよい.Reduceを使うとこれが分かる.
ReduceとSolveの基本的な違いは,Reduceでは与えた方程式について可能なすべての解が求まるのに対して,Solveでは「一般的な」解だけが求まる.ここで,一般的な解とは,解法の対象になった変数に関連した条件は考慮するが,他のパラメータに関する条件は入らない解を意味する.さらに,ReduceとSolveの違いに,解の出力形式としてReduceが等式の組合せとして解を返すのに対して,Solveは変換規則として返すということもある.
Solveを使い,任意の一次方程式を解く:
一般二次方程式の持つすべての解を求める.結果として3組の解が得られる.aが0以外のとき,二次方程式はxについて2つの解を持つ.aが0のとき,方程式は一次式になる.また,a,b,cが0のとき,xの値は何でもよい:
存在する解は一般的な解ではないので,Solveを使うと何も求まらない:
方程式が常に成立するとき,Solveの返す解はこのように表記される:
Solveでは解けず,一般的な解は存在しないことが分かる:
Solveでは解が求まらず,一般的な解が存在しないことが分かる:
それでも,Reduceを使うと,解が存在するための条件が得られる:
Wolfram言語で連立方程式を設定するということは,変数と変数の間に制約条件を設ける,ということになる.一般的に言って,Solveを使うということは,与えられた方程式の制約条件に従いながら,変数のうちのいくつかを用いて残りの変数を表現することである.
特定の変数を消去した明示的な方程式がほしい場合もある.そのときにはEliminateを使う.
方程式の集合を取り扱う際,よく,特定の文字を真の「変数」としてとらえ,他は「助変数(パラメータ)」とみなすようにする.そのとき,変数間の特定の関係が常に満たされるのは,パラメータがどのような値を取るときであるかということを知る必要が生ずることもある.
| SolveAlways[eqns,vars] | 方程式 eqns を任意の vars の値について常に満足させるようなパラメータの値を求める |
| x==y | x は y に等しい(xy としても入力可) |
| x!=y | x は y に等しくない(x≠y としても入力可) |
| x>y | x は y より大きい |
| x>=y | x は y に等しいより大きい(x≥y としても入力可) |
| x<y | x は y より小さい |
| x<=y | x は y に等しいより小さい (x≤y としても入力可) |
| x==y==z | すべて等しい |
| x!=y!=z | すべて等しくない(全部違う値) |
| x>y>z 等 | 真に減少 |
すべての数が違うわけではない.したがって,Falseになる.
両方とも数値的な量を表すので,Wolfram言語は,この関係がTrueであると判断できる.
| !p | 否定(¬pとしても入力可) |
| p&&q&&… | 論理積 (p∧q∧…としても入力可) |
| pq… | 論理和(p∨q∨…としても入力可) |
| Xor[p,q,…] | 排他的論理和(p⊻q⊻…としても入力可) |
| Nand[p,q,…] と Nor[p,q,…] | 否定論理積と否定論理和(⊼ および ⊽ としても入力可) |
| If[p,then,else] | |
| LogicalExpand[expr] | 論理演算式を展開する |
2つの関係は同時に正しいので,Trueの結果が得られる.
LogicalExpandを作って項を展開してみる.
Solveにより3つの解が返される:
| eqns1eqns2 | 解の集合の和集合 |
| eqns1&&eqns2 | 解の集合の交わり |
| !eqns | 解の集合の補集合 |
| Implies[eqns1,eqns2] | eqns2を含む eqns1の部分集合 |
「演算子」で説明してあるように特別な論理結合記号を用いると便利なことがある.
方程式x^2+3x==2はx^2+3xが2と等しいことを表すように,不等式x^2+3x>2はx^2+3xが2より大きいことを表す.Wolfram言語では,Reduceは方程式だけでなく不等式にも使用できる.
| Reduce[{ineq1,ineq2,…},x] | x における不等式の組を約す |
Reduce[ineq,x]は,方程式に適用されると x==r1, …という形式の x についての単純な方程式からなる結果を得ようとする.Reduce[ineq,x]は不等式に適用されても全く同じことをしようと試み,l1<x<r1, …という形式の x についての単純な不等式からなる結果を得ようとする.
Reduce[ineq,x]によって生成された結果は,不等式で表現された一連の区間を表すものだと考えることができる.次数 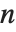 の多項式のグラフは最高
の多項式のグラフは最高 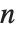 回まで上下できるので,次数
回まで上下できるので,次数 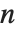 の多項不等式は最大
の多項不等式は最大 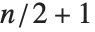 の異なる区間を誘発することができる.
の異なる区間を誘発することができる.
この不等式を解くためにはProductLogを導入する必要がある:

Reduceは次のようにして無限個の区間を表す:
| Reduce[{ineq1,ineq2,…},{x1
,
x2
,
…
}]
| 不等式の組をいくつかの変数に約す |
多変量の不等式の場合,Reduceは実際には区間指定のネストした組を与える.この指定では後の方の変数は前の方の変数に依存する境界を持つ.
幾何学的な用語を使えば,いかなる線形不等式も空間を二等分する.ゆえに,線形不等式のリストは境界があったりなかったりする多面体を定義する.Reduceはそのような多面体をネストした不等式で表す.多面体の頂点は常にこれらの不等式の終点に当たる.
パラメータを含む不等式の場合,Reduceは方程式の場合と同じように起りうる個々のケースを自動的に処理する.
| FindInstance[ineqs,{x1,x2,…}] | ineqs を満足する xi の例を求めようとする |
| FindInstance[ineqs,vars,n] | n 個の例を求めようとする |
FindInstanceと不等式の関係はSolveと等式の関係に例えることができ,Solveのように変数の特定の値を与える規則のリストを返す.しかし,方程式の場合はこれらの値が一般的にすべての解を正確に表すのに対し,不等式の場合は不等式によって記述された領域内の孤立したサンプル点に相当するに過ぎない.
特定の入力で呼ばれるたびにFindInstanceは同じ出力を返す.そして,特別の限定的な何らかの点に対応する例が存在する場合はそれらを優先的に返す.しかし一般的にはFindInstanceが返す例の分布は大抵の場合ランダムに見える.だが,各々の例は実際には与えた不等式が実際に満足できることの建設的な証明となっている.
円板上のある一点を求めるとFindInstanceは原点を返す:
Wolfram言語は通常,方程式の変数は任意の複素数を表すことができると仮定する.しかしReduceを使うときは変数がもっと限定された領域内のオブジェクトを表すことを明示的にWolfram言語に伝えることができる.
しかし変数が増えると,ある変数の値が他の変数の値に依存するといったようなことが起り得るパラメトリックな曲線や曲面に方程式の解が対応し,途端に話は複雑になる可能性がある.このような依存関係はしばしば方程式あるいは不等式の集合で表現される.しかし,その形式はある領域から別の領域に移動すると甚だしく変化することがある.
入力に含まれるのが等式のみであれば,Reduceはデフォルトによってすべての変数が複素数であると仮定する.しかし入力に不等式が含まれている場合は,不等式は実数のみしか比較できないのでReduceは含まれる代数的変数はどれも実数であると仮定する.
原則としてReduceは実変数と複素変数を持った整方程式と不等式のどのような集合についても常に完全な解を求めることができるが,変数の数が増えるにつれて要素の数が指数関数的に増加するため,結果は非常に複雑になることが多い.
SinやExpのような関数を導入した途端に,変数が実変数あるいは複素変数1つの方程式でも解の要素が無限になることがある.Reduceは新たなパラメータを導入してこれらの要素にラベルを付ける.デフォルトでは与えられた解の 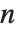 番目のパラメータにC[n]という名前が付けられる.一般的には,オプション設定GeneratedParameters->f を使ってそれが f[n]という名前になるように指定することができる.
番目のパラメータにC[n]という名前が付けられる.一般的には,オプション設定GeneratedParameters->f を使ってそれが f[n]という名前になるように指定することができる.
Reduceは実変数と複素変数を持つ方程式だけでなく整数領域の方程式も扱うことができる.ディオファントス(Diophantus)方程式のようなものを解くのは大変難しいことが多い.
Reduceは整数領域のどのような線形方程式の系も不等式の系も解くことができる.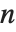 変数の
変数の 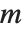 個の線形方程式では,一般に
個の線形方程式では,一般に  個のパラメータが必要である.しかし不等式の場合ははるかに多くのパラメータが必要なことが多い.
個のパラメータが必要である.しかし不等式の場合ははるかに多くのパラメータが必要なことが多い.
変数が2つの場合,Reduceは整数についてのいかなる二次方程式も解くことができる.結果はフィボナッチ列に類似しており二次無理数のベキによって表される.
以下は特定のC[1]の整数値における値である:
Reduceは整数についての方程式の多くの特定のクラスを扱うことができる.
ここでReduceを使ってThue方程式の解を求める:
実数と複素数についての整方程式の場合,解が存在するかどうかを決定するための確かな「アルゴリズム」が存在する.しかし整数についての整方程式の場合は,ヒルベルト(Hilbert)の第10問題が解けないことから分かるように,そのような一般的な方法は決して存在しない.
特定のクラスの方程式の場合は,そのようなアルゴリズムを見付けるのは可能であり,実際に多くがReduceに実装されている.しかし異なったクラスの方程式を扱うことは数論の全く違った分野と全く違った種類の計算を必要とするように見えることが多い.実際に,いくつかの変数を埋めることにより,他の変数の解が可能なすべてのプログラムの出力に対応するようにできる「普遍的な」整数の整方程式の存在が知られている.ここから,このような方程式には一般的に代数関数のように固定要素によって構築される解で構成される閉じた形は決して存在しないことになる.
Sinのような関数が含まれるようにすると,実数と複素数を含む方程式についても同じ問題が起り得る.
ここのReduceは事実上整数についての方程式を解かなくてはならない:
Reduceはいくつかの異なる剰余を持つ方程式を扱うことができる.
Reduceは通常複素変数を単一のオブジェクトとして扱う.しかし,解析的ではなかったり分岐切断線を持つ関数を扱う際は,複素変数を実数部分Re[z]と虚数部分Im[z]の2つの部分に分割する必要があることがある.
Reduceはデフォルトにより不等式に代数的に表れる数は実数であると仮定する.しかしComplexesをデフォルトの領域として明示的にこれを上書きすることもできる.そのような場合は特定の変数がなお実数であると指定することができると便利である.
| FindInstance[expr,{x1,x2,…},dom] | expr を満足する dom 中の xi の例を見付けようとする |
| FindInstance[expr,vars,dom,n] | n 個の例を見付けようとする |
| Complexes | 複素数 |
| Reals | 実数 |
| Integers | 整数 |
| Booleans |
FindInstance[expr,vars,dom]が{}を返した場合は,expr が指定領域にある変数のいかなる値によっても満足されないことをWolfram言語が事実上証明したことを意味している.expr が満足される場合は,「方程式と不等式の操作:不等式」の不等式についての項で説明してあるように,FindInstanceは一般に極めて恣意的に満足する値を取り出す.
特に整数方程式の場合,たとえReduceが完全な解を求めることができなくても,FindInstanceが方程式の特定の解を求めることができることがしばしばある.そのような場合には方程式の最も小さな解のうちのいずれかが返される.
FindInstanceの特徴のひとつに,変数がTrueあるいはFalseという値を持ち得るブール式と一緒にも使える点が挙げられる.式がTrueとなるような変数の真理値が選べるようにFindInstanceを使って特定の式が「満足可能」であるかどうかを検証することができる.
方程式や不等式のいかなる組合せも,何らかの空間における領域を暗示的に定義しているものと考えることができる.Reduceの基本的な機能はこの種の暗示的な表示を明示的にすることである.
変数の値によって指定された点が領域内にあるかどうかをテストするだけなら,方程式や不等式についての記述が暗示的であっても問題ない.しかし,領域の構造を理解するためには,あるいはその中で点を生成するためには,Reduceが提供するようなより明示的な説明が必要であろう.
Reduceはこの領域をより明示的に表す:
Reduce[expr,{x1,x2,…}]は,まず最初に x1についての固定した条件を与え,次に x1に依存する x2についての条件を与え,次に x1と x2に依存する x3についての条件を与え,というようにして領域を表現するようになっている.この構造には,Tableのような関数で反復子を使うのと同じように各 xi の値を連続的に選ぶことで点が選べるという特徴がある.
単純なケースでは,方程式あるいは不等式の系によって定義された領域に結局要素が1つしかないことがある.そのような場合はReduceの出力は e1&&e2…の形式になる.ここで各 ei は最高 xi 個までの変数を含む方程式か不等式である.
しかし,ほとんどの場合には複数の要素が u1u2…のような形式を含む出力で表される.Reduceは領域を表すために使う要素数を最小にしようとする.しかし場合によっては単一の接続した要素をカバーするのに複数のパラメータ化が必要なこともある.その各々はReduceの出力中で別々の要素として現れる.
解の集合を表す際に,複数の要素が…&&(u1u2)&&…のような形式を使って一緒に表現できることがある.Reduceは結果をできるだけコンパクトにするためにデフォルトでこれを行う.LogicalExpandを使って各要素が別々に現れる展開された形を生成することもできる.
最もコンパクトな形を生成するために,Reduceは必要以上に後半の変数 xi が前半の変数 xi に依存する条件を課してしまうことがある.オプションBacksubstitutionTrueを与えることで,特定の xi がより前の変数 xi に必要最低限しか依存しないような結果をReduceに生成させることができる.こうすると解釈しやすくなることがあるが,出力ははるかに大きくなることが多い.
| CylindricalDecomposition[expr,{x1,x2,…}] | |
expr により定義された領域の円筒代数分解を生成する | |
| GenericCylindricalDecomposition[expr,{x1,x2,…}] | |
expr で定義された領域の分解の全次元の部分と,領域の残りの部分を含む超曲面とを見付ける | |
| SemialgebraicComponentInstances[expr,{x1,x2,…}] | |
expr により定義された各連結成分に少なくとも1つの点を与える | |
実数領域の整方程式や不等式の場合,Reduceが返す結果の形式は通常「円筒代数分解」すなわち「CAD」である.Reduceはより単純な形を与えることもある.いずれにせよ,CylindricalDecompositionを使うことで完全なCADを得ることができる.不等式のみを含む系では,GenericCylindricalDecompositionで解集合のほとんどが求められ,通常こちらの方が速い.
x^4+x^2>0のような命題で,Wolfram言語は変数xを特定はされていないが限定的な値を持つものとして扱う.しかし,場合によってはxが取り得る可能な値の集合についての陳述を行うことができると便利である.そのような場合には「限定子」を使うとよい.
| ForAll[x,expr] | x のすべての値で成り立つ expr |
| ForAll[{x1,x2,…},expr] | すべての xi のすべての値で成り立つ expr |
| ForAll[{x1,x2,…},cond,expr] | cond を満たすすべての xi で成り立つ expr |
| Exists[x,expr] | expr が成り立つ値 x が存在する |
| Exists[{x1,x2,…},expr] | expr が成り立つ複数の値 xi が存在する |
| Exists[{x1,…},cond,expr] | cond を満たす expr が成り立つ複数の値 xi が存在する |
Wolfram言語では方程式,不等式,論理結合等と同じように量限定子も扱うことができる.ほとんどの場合,量限定子は評価によってすぐに変化はしない.しかし,FullSimplifyやReduceのような関数を使って量限定子を簡約することができる.
FullSimplifyによって宣言が真であることが確認される:
Wolfram言語は述語論理と純粋数学で使われている量限定子の標準的な表記によるバージョンをサポートしている.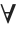 は\[ForAll]あるいはEscfaEscとして入力できる.また,
は\[ForAll]あるいはEscfaEscとして入力できる.また,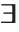 は\[Exists]あるいはEscexEscとして入力できる.表記を厳密にするために,Wolfram言語は限定子の付いた変数を下付き文字にする.変数の条件もまたコンマで区切った下付き文字にする.
は\[Exists]あるいはEscexEscとして入力できる.表記を厳密にするために,Wolfram言語は限定子の付いた変数を下付き文字にする.変数の条件もまたコンマで区切った下付き文字にする.
| ∀xexpr | ForAll[x,expr] |
| ∀{x1,x2,…}expr | ForAll[{x1,x2,…},expr] |
| ∀x,condexpr | ForAll[x,cond,expr] |
| ∃xexpr | Exists[x,expr] |
| ∃{x1,x2,…}expr | Exists[{x1,x2,…},expr] |
| ∃x,condexpr | Exists[x,cond,expr] |
量限定子を含む命題を,量限定子を除去した等価の命題に変換できる場合がある.量限定子の除去は,すべての x あるいは特定の x について真であるという黙示的な宣言を,これが成立する条件に関する明示的な宣言に変換する点で,方程式を解くのに似ている.
Resolveは,複素領域と実数領域の任意の整方程式と不等式から常に量限定子を除去することができる.また論理式からも量限定子が除去できる.
Reduceでも量限定子を使うことができる.Reduceに方程式あるいは不等式の集合を与えると,Reduceは完全な解の集合の詳細に渡る表現を作成しようとする.しかし,ときには解が x のすべての値を網羅している,あるいはこの値を全くカバーしていないといった,より大域的な問いに対する答がほしい場合もあるだろう.量限定子は,このような問いを指定する便利な方法を提供している.
| Minimize[expr,{x1,x2,…}] | expr を最小にする |
| Minimize[{expr,cons},{x1,x2,…}] | 制約条件 cons に従って expr を最小にする |
| Maximize[expr,{x1,x2,…}] | expr を最大にする |
| Maximize[{expr,cons},{x1,x2,…}] | 制約条件 cons に従って expr を最大にする |
Minimize[expr,x]は x を から
から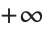 のすべての可能な値の範囲で expr を最小にする.Minimize[{expr,cons},x]は制約条件 cons が満足されるという条件の下で expr を最小にする.制約条件は方程式と不等式のどのような組合せでもよい.
のすべての可能な値の範囲で expr を最小にする.Minimize[{expr,cons},x]は制約条件 cons が満足されるという条件の下で expr を最小にする.制約条件は方程式と不等式のどのような組合せでもよい.
MinimizeとMaximizeの重要な特徴は,これらが常に「大域的」最小値と最大値を求められる点である.関数はそこで導関数が消失するさまざまな極大値と極小値を持つことが多い.しかし,MinimizeとMaximizeは大域的な方法を用いて極小値と極大値だけでなく絶対最小値と絶対最大値も求める.
Maximizeは大域的最大値を求める:
境界を持たない関数を与えるとMinimizeとMaximizeは と
と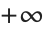 を最小と最大として返す.また,決して満足し得ない制約条件を与えると,
を最小と最大として返す.また,決して満足し得ない制約条件を与えると,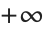 と
と が最大と最小として返され,Indeterminateが変数の値として返される.
が最大と最小として返され,Indeterminateが変数の値として返される.
MinimizeとMaximizeは  という形式の「厳密ではない」不等式と
という形式の「厳密ではない」不等式と  という形式の「厳密な」不等式の両方を受け入れる.厳密ではない不等式の場合,最小と最大が境界
という形式の「厳密な」不等式の両方を受け入れる.厳密ではない不等式の場合,最小と最大が境界  上にあっても全く問題ないが,厳密な不等式の場合は最小と最大は原則として少なくともほんのわずかでも境界の内側になければならない.
上にあっても全く問題ないが,厳密な不等式の場合は最小と最大は原則として少なくともほんのわずかでも境界の内側になければならない.
| MinValue[{f,cons},{x,y,…}] | 制約条件 cons を前提として f の最小値を与える |
| MaxValue[{f,cons},{x,y,…}] | 制約条件 cons を前提として f の最大値を与える |
| ArgMin[{f,cons},{x,y,…}] | 制約条件 cons を前提として f が最小化される位置を与える |
| ArgMax[{f,cons},{x,y,…}] | 制約条件 cons を前提として f が最大化される位置を与える |
Maximizeは最大の値と位置の両方を与える:
最大値だけが必要な場合はMaxValueを使う:
ArgMaxは最大値が得られた位置を与える: