操作方程和不等式

方程消去变量
解方程关系运算符和逻辑运算符
方程和解的表示求解逻辑组合的方程组
一元方程不等式
多项式根的计数及隔离不同域上的方程和不等式
代数数解集的表示法
联立方程组量词
通解和非通解最小化和最大化
方程
"定义变量" 讨论赋值问题，例如 x=y 给 x 赋以值 y. 本节讨论方程，检验相等性. 方程 x==y 检验 x 是否等于y.
检验 2+2 和 4 是否相等. 产生的结果是符号 True：
区分清楚 x=y 和 x==y 是很重要的. x=y 是强制进行赋值操作的声明，而 x==y 只检验 x 和 y 是否相等，而不引起明确的行动. 使用过C语言的用户会看出 Wolfram 语言的赋值和检验表示法与 C 语言是相同的.
x=y
给 x 赋以值 y
x==y
检验 x 和 y 是否相等
赋值和检验.
给 x 赋以值 4：
如果查看 x，则得到4：
检验 x 是否等于4. 在这个情况下，结果为真：
检验发现 x 等于 4，不等于 6：
清除赋给 x 的值：
到此为止，我们使用的检验仅涉及到数，并且总能得到确定答案，True 或者 False. 然而，用户也能对符号表达式进行检验.
Wolfram 语言不能得到这个检验的确定结果，除非你已赋给 x 一个特定的数值：
当用 4 代换 x 时，检验结果为 False：
甚至当用户检验符号表达式时，有时也能得到确定结果. 例如，当用户检验两个恒等式时，无论表达式中的变量是什么数值，Wolfram 语言都知道该两个表达式是相等的.
不论 x 为何值，这两个表达式都相等，所以结果为 True：
Wolfram 语言并不检验这两个表达式是否相等. 此时，使用 Expand 将使他们有相同的形式：
在 Wolfram 语言中，如 x==4 这样的 表达式代表方程式. Wolfram 语言中有许多处理和求解方程的函数.
Wolfram 语言中的一个方程. 在 "解方程" 中讨论如何求解 x：
给方程赋一个名称：
查看 eqn，将得到该方程：
解方程
一个表达式如 x^2+2x-7==0 表示 Wolfram 语言中一个方程. 求解这样的方程是人们常常要做的事情，就是要找出对于什么 x 值，表达式为真.
给出二次方程 的两个解. 以 x 的代换形式给出：
解的近似值：
通过使用 Solve 生成的 x 的替代算符规则，可以得到 x 的实际的解：
可以把这个规则用于任何含有 x 的表达式：
Solve[lhs==rhs,x]
解方程，给出 x 的替换规则列表
x/.solution
使用替换规则得到 x 的值
expr/.solution
使用规则得到表达式的值
求和使用方程的解.
解方程时，Solve 总试图给出精确的解析解. 然而，根据数学的基本结论，对很复杂的方程是求不出解析解的. 在解一元代数方程时，如果变量的最高次数不超过4，那么 Wolfram 语言总能给出解析解. 但如果最高次数是 5 或更高，给出精确解析解在数学上一般是不可能的.
Wolfram 语言总能求出次数小于5的一元代数方程的解析解：
也可以求解某些较高次数的方程：
对那些在数学上不可能求出精确解析解的方程，Wolfram 语言使用 Root 对象表示方程的解：
虽然得不到精确解析解，但可以求出数值解：
除了能解纯代数方程，Wolfram 语言还能求解其他一些函数方程.
Wolfram 语言返回方程的完整解：
打印警告后，Wolfram 语言返回方程的一个解：
重要的是要意识到方程例如， 实际上有无数个解. 但是，默认情况下，Solve 只返回一个解，但是打印消息告诉你可能存在其他解. 可以使用 Reduce 获取更多信息.
对这样的超越方程没有“精确形式”的解：
使用函数 FindRoot，给出 x 的初始值，可求得近似解：
函数 Solve 也能处理具有符号函数的方程. 在此情况下，又显示一个警告，然后给出形式上的反函数的结果.
Wolfram 语言使用 f 的形式上的反函数给出计算结果：
Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}]
关于变量 x，y，… 求解方程组
解方程组.
使用 Wolfram 语言也能解联立方程组. 只须给出方程组，并指明关于哪些变量求解即可.
两个联立方程，关于变量 x 和 y 求解：
更复杂的联立方程组. 两个解以 x 和 y 的替换形式的列表给出：
使用上述解计算表达式 x+y：
Wolfram 语言能够解任何线性方程组. 也可以解多种类型的多项式方程组.
当求解含有多个变量的方程组时，通过消去一些变量来整理方程往往是很方便的.
在两个方程中消去 y，得到关于 x 的单个方程：
如果有几个方程，则不能保证一定有解.
这个方程组无解，故 Wolfram 语言给出返回值 {}，表明解集是空的：
对 a 的几乎所有值，这个方程组都没有解：
一个方程组是否有解是一个很不清楚的问题. 例如，对 a 的大多数值，方程组 {x==1,x==a} 是不相容的，所以关于 x 无解. 然而，如果 a 等于 1，则方程有一个解. 函数 Solve 被设置为求方程的一般解. 不考虑那些仅对参数的特殊值才存在的解.
如果使用 Reduce 而非 Solve，Wolfram 语言将求出方程组的所有可能的解，包括那些对参数有特殊要求的解.
这里显示了仅当 a==1 时，方程组有一个解. a==1&&x==1 表示要求 a==1 和 x==1 都为 True：
这里给出了方程的所有可能解. 答案被表达为简单方程的组合. && 表示必须同时成立，|| 表示二中择一：
一个更复杂的方程的组合：
给出所有解的符号表示：
Solve[lhs==rhs,x]
关于 x 求解方程
Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}]
关于 x，y，… 求解联立方程组
Eliminate[{lhs1==rhs1,lhs2==rhs2,…},{x,…}]
在联立方程组中，消去 x，…
Reduce[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}]
给出一组简化方程，包括所有可能的解
求解和处理方程的函数.
Reduce 对专门在实数或整数范围内处理方程也具有强大的功能. "不同域内的方程和不等式" 节将更详细讨论这个问题.
假定 x 和 y 是复数，简化方程：
包含对 x 和 y 必须为实数的要求条件：
只给出整数解：
方程和解的表示
Wolfram 系统将方程作为逻辑语句处理. 如果键入一个方程如：x^2+3x==2，那么 Wolfram 系统将其解释为声明x^2+3x 等于 2 的语句. 如果已经明显地给 x 赋了值，如 x=4，那么 Wolfram 系统能确定逻辑声明x^2+3x==2 为 False.
然而，如果没有明显给 x 赋值，那么 Wolfram 系统不能确定 x^2+3x==2 是 True 还是 False. 因此保持方程的符号形式 x^2+3x==2.
在 Wolfram 系统中，有许多方法处理符号方程. 一个常见的目标是重新整理方程以便 “求解” 一组特定的变量.
一个符号方程：
使用函数 Reduce 可以简化方程，以给出 x 的 “解”. 结果如同原先的方程一样，可以被视为一个逻辑语句：
二次方程 x^2+3x==2 可以看作关于 x 值的隐式描述. 综合上述例子所示，可以使用函数 Reduce 得到 x 值的显式描述. 由 Reduce 生成的表达式为 x==r1||x==r2 的形式. 这还是一个逻辑语句，声明 x 等于 r1，或 x 等于 r2. 这个语句给出的 x 值与原方程给出的 x 值是完全一样的. 然而多数情况下，Reduce 给出的形式比原方程更有用.
可以像其他逻辑语句一样组合和处理方程. 可以使用逻辑连接，诸如 || 和 && 去指定选项或联立的条件. 可以使用如LogicalExpand 和 FullSimplify 这样的函数化简方程集合.
多数情况下，把方程简单地作为逻辑语句处理是方便的. 但有时在其他运算中，用户实际上想使用方程的显式解. 此时，将形如 lhs==rhs 的方程转换为形如 lhsrhs 的变换规则是方便的. 一旦有了方程的具有显式变换规则形式的解，就可以使用算符 /. 将解代入表达式.
Reduce 生成相应于二次方程根的 x 值的逻辑语句：
ToRules 将逻辑语句转换为变换规则的显式列表：
现在可以使用变换规则将 x 的解代入含有 x 的表达式中：
函数 Solve 直接生成解的变换规则：
一元方程
Solve 和相关的 Wolfram 语言函数处理的方程主要是多项式方程.
求解 x 的线性方程是容易的：
通过使用简单的公式也可以求解二次方程：
Wolfram 语言也能求三次方程的精确解. 这里是方程的第一个解：
对三次或二次方程，结果常常是复杂的. 但对次数不超过四次的方程，Wolfram 语言总能给出解的显式公式.
这些公式的一个重要特点是他们仅包含根式 ：二次根、三次根和较高次根的算术组合.
然而，作为基本的数学事实，五次及五次以上的方程，一般不再可能给出仅含根式的解的显式公式.
虽然在一些特殊情形可以做到这一点，但绝大多数情形是不行的.
构造一个6次多项式：
对于这种能分解因式的多项式，Solve 直接求出根：
构造一个8次多项式：
这个多项式不能分解多项式，但能分解成嵌套多项式，所以 Solve 也能求出根的显式公式：
Root[f,k]
方程 f[x]==0 的 k 次根
根的隐式表示.
对这个方程不能给出仅含根式的解的显式公式，所以 Wolfram 语言使用一个隐式符号表示：
求每个根的数值近似解：
如果用户最终想要数值解，那么使用 NSolve 将快得多：
Root 对象提供一个精确的，尽管是隐式的，多项式的根的表示. 用户可以像使用 Sqrt[2] 或其他代表精确数值量的表达式一样使用根对象.
这里是上面讨论的多项式的第一个根的 Root 对象：
数值近似值：
函数 Round 使用精确计算求出最接近这个根的整数：
如果将根式代入原多项式并化简结果，将得到0：
求出原多项式所有根的连乘：
第三个根的复共轭是第二个根：
如果求解的方程中仅有的符号参数是待求变量，那么，方程的所有根都是数. 但方程中如果有其他符号参数，那么解将是这些参数的函数.
这个方程的解还是用 Root 对象表示，但现在每个 Root 对象包含参数 a：
当取 a 等于 1 时，Root 对象被化简，其中一些由显式根式给出：
显示第一个根作为 a 的函数的变化情况：
求第一个根关于 a 的导数：
给 Solve 任何 次多项式方程，总能返回 个解，尽管其中一些可能用 Root 对象代表. 如果有退化解，那么每个解出现的次数将等于他的重数.
Solve 给出此方程的两个相等的解：
一个10次方程的前4个解，这些解成对出现：
Wolfram 语言还能求解不明显是多项式形式的方程.
包含平方根的方程：
包含对数的方程：
只要一个方程能化为某种多项式形式，Wolfram 语言总能用 Root 对象代表他的解. 但是，对更一般的方程，比如包含超越函数的方程，没有使用 Root 对象，甚至没有求数值近似值的系统方法.
关于 x 的简单超越方程：
关于标准函数，该方程没有解：
在这种情况下，Wolfram 语言还可以求出一个数值解：
单变量的多项式方程组只有有限数目的解. 但是，超越方程往往有无穷多解. 通常的原因是，超越函数实际上有无穷多可能的逆函数. 使用默认选项设置 InverseFunctionsTrue，Solve 将假定任何这种函数有确定的逆函数. Solve 可能能够关于此逆函数返回特定的解.     
Wolfram 语言关于 ProductLog 返回特定的解，但显示警告说明其他的解可能被丢失：
如果要求 Solve 求解一个包含任意函数如 f 的方程，在默认情况下，将试图构建一个关于逆函数的正式解.
默认情况下，Solve 对函数 f 使用正式的逆函数：
逆函数的结构：
InverseFunction[f]
f 的逆函数
InverseFunction[f,k,n]
具有 n 个参数的函数 f 关于第 k 个参数的逆函数
逆函数.
返回一个显式的逆函数：
Wolfram 语言可以在逆函数上进行正式操作：
虽然 Solve 只能给出一个方程的具体解，Reduce 可以给出整个解集的表示法. 对于超越方程，最终往往引入新的参数，取值包括所有可能的整数.
解集的完整表示：
一般解的表示：
正如 "不同域上的方程和不等式" 中更多篇幅的讨论，Reduce 允许用户限制变量的域. 有时候，这将产生超越方程的确定解——或者表明他们不存在.
如果限制 x 的域，将产生确定的解：
如果限制 x 为实数，只可能有一个解：
Reduce 知道这里不可能有解：
多项式根的计数及隔离

计算多项式根的数目

CountRoots[poly,x]
给出多项式 poly 关于 x 的实数根的数目
CountRoots[poly,{x,a,b}]
给出多项式 poly 关于 x 满足 的根的数目
计算多项式根的数目.
CountRoots 接受具有高斯有理数系数的多项式. 根的数目包含了重数.
给出 的实数根的数目：
计算 在闭区间 内的根的数目：
在垂直轴 和 之间的部分的根包含了在 的三重根和在 的单根：
计算在闭单位正方形内的17次单位根的数目：
多项式的系数可以是高斯有理数：

隔离区间

一个集合 ，其中 是 或者 ，是多项式 的一个根 的 隔离 区间，如果满足 是 在 内的唯一根. 多项式根的隔离意味着找到多项式所有根的不相交的隔离集合.
RootIntervals[{poly1,poly2,…}]
给出任何一个多项式 polyi 的实根的不相交隔离区间的列表，连同一个有关与每个相连的根对应的是哪个多项式的列表
RootIntervals[poly]
给出单个多项式的实根的不相交隔离区间
RootIntervals[polys,Complexes]
给出 polys 的复数根的不相交隔离区间或矩形
IsolatingInterval[a]
给出代数数 a 的一个隔离区间
IsolatingInterval[a,dx]
给出一个宽度至多为 dx 的隔离区间
多项式的隔离根的函数.
RootIntervals 接受具有有理数系数的多项式.
对于一个实根 ，返回的隔离区间是一个有理数对 ，使得 或者 . 对于一个非实根 ，返回的隔离矩形是一对高斯有理数 ，使得 以及 或者 .
的实根的隔离区间：
第二个列表表明哪个区间包含了哪个多项式的根：
给出 的所有复数根的隔离区间：
这是3次和4次的单位根的隔离区间. 第二个区间包含对于两个多项式相同的根：
下面是一个7次的多项式的一个根的隔离区间：
给出一个宽度至多为 的隔离区间：
该区间的所有数都具有相同的前10位小数.
代数数
Root[f,k]
多项式方程 f[x]==0 的 k 次根
代数数的表示.
当输入一个 Root 对象时，其中的多项式自动被化简为极小形式：
提取出代表多项式的纯函数并用于 x：
Root 对象是 Wolfram 语言表示代数数的方式. 代数数有这样的性质：当对其进行代数运算时，总是得到单个代数数.
一个代数数的平方根：
RootReduce 将其化简为单个 Root 对象：
一个包含代数数的更复杂的表达式：
还是能被化简成单个 Root 对象，尽管是相当复杂的：
RootReduce[expr]
尝试化简 expr 为单个 Root 对象
ToRadicals[expr]
尝试转换 Root 对象为显式根式
代数数的运算.
在这种简单情形下，Root 对象自动表示为根式：
当包含三次多项式时，Root 对象不能自动表示为根式：
ToRadicals 尝试用根式表示所有的 Root 对象：
如果 Solve 和 ToRadicals 不能成功地用根式表示某多项式方程的解，那么可以猜测其本质上是做不到的. 但应当认识到，有些特殊情形，化为根式在原理上是可能的. 但 Wolfram 系统找不到. 最简单的例子是方程 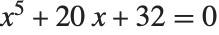，但这里用根式表示的解是非常复杂的. 方程 是另一个例子，此时 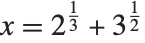是一个解.
给出一个包含6次多项式的 Root 对象：
尽管存在单个的根式形式，ToRadicals 找不到：
4次以上的大多数多项式没有能用根式表示的根. 然而，5次时，根总能用椭圆或超几何函数表示. 但是结果太复杂，实际上是没有用的.
RootSum[f,form]
对满足多项式方程 f[x]==0 所有 求 form[x] 的和
Normal[expr]
具有 RootSum 的 expr 用 Root 对象的显式和式代替的形式
根的和.
计算 的根的倒数的和：
此式没有用根式表示的显式结果：
将 RootSum 展开成为包含 Root 对象的显式和：
RootApproximant[x]
把数字 x 转换成一个近似的“最简单”的代数数
RootApproximant[x,n]
求近似 x 的次数不超过 n 的代数数
从数值上逼近来复原 ：
在这种情况下，结果的次数不超过4：
确认 Root 表达式对应于 ：
联立方程组
Solve 可以解联立方程组. Solve 可以求一大类联立多项方程组的显式解.
具有两个未知量的简单线性方程：
更复杂的例子. 结果是一个解的列表，每个解由变量变换规则的列表构成：
可以使用带有 /. 算符的解的列表：
即使当 Solve 不能求出显式解时，也常常能“展开”联立方程组，使用 Root 对象生成一个符号结果：
可以使用 N 得到数值结果：
在 Solve 中使用的变量不必是单个符号. 通常当建立大的联立方程组时，可以使用如 a[i] 这样的表达式作为变量.
关于 a[i] 的三个方程的列表：
关于某些 a[i] 求解：
Solve[eqns,{x1,x2,…}]
关于特定的对象 xi 求解 eqns
Solve[eqns]
关于 eqns 中的所有对象求解 eqns
求解联立方程组.
如果不明显地指出要求解的对象，Solve 将对所有变量求解：
■ Solve[{lhs1==rhs1,lhs2==rhs2,…},vars]
■ Solve[lhs1==rhs1&&lhs2==rhs2&&…,vars]
■ Solve[{lhs1,lhs2,…}=={rhs1,rhs2,…},vars]
给 Solve 提供联立方程组的几种方法.
当使用矩阵构造联立方程组时，得到的是表达式的列表之间的等式：
Solve 将包含列表的方程转换为方程的列表：
可以使用 LogicalExpand 直接做转换：
在某些类型的计算中，可以方便地使用系数数组而非显式方程. 用户可以使用 CoefficientArrays 从方程构造数组.
通解和非通解
如有一个方程 2x==0，显然仅有的解是 x0. 但是如果有方程 ax==0，事情就不那么清楚了. 当 a 不等于零时，仍然有唯一解 x0. 然而，当 a 实际上等于零时，那么 x 的任何值都是解. 可以使用 Reduce 查看这些功能.
Solve 隐含假定参数 a 不为 0：
然而，Reduce 给出所有的可能性，不做任何关于 a 值的假定：
Reduce 和 Solve 之间最重要的区别在于 Reduce 给出方程组的全部解，而 Solve 仅给出通解. 通解是指只涉及要求的变量条件，而不涉及方程中参数的条件. Reduce 和 Solve 的另一个区别是 Reduce 总是返回方程的组合，而 Solve 给出变换规则形式的结果.
Solve[eqns,vars]
求方程的通解
Reduce[eqns,vars]
化简方程，保留全部解
解方程.
Solve 给出的任意线性方程的解：
Reduce 给出其全部解，包括 a==b==0 的可能性. 注意，输出中 && 比 || 的优先级高：
一般二次方程的全部解. 有三种选择. 当 a 不等于零时，由标准二次公式给出 x 的两个解. 当a 等于零时，方程退化为线性方程. 最后如果 a，b ，c 全为0，则对 x 无限制：
当用户具有一些联立方程组时，Reduce 可以发现在什么条件下方程组有解. 而 Solve 则告诉用户是否存在通解.
方程组无解：
方程组仅当 a 取特殊值 1 时有一个解：
该解不是通解. 故被 Solve 拒绝：
若限制 a 等于 1，那么 Solve 也能给出解：
此方程对任何 x 值都成立：
当方程对任何值都成立时，Solve 返回的结果：
对于线性方程组，可以使用 Solve 得到通解，使用 Reduce 弄清参数在什么值下解存在.
一个矩阵，其第 个元素是 ：
矩阵的行列式为零：
建立三个方程的联立方程组：
Solve 报告没有通解：
然而，Reduce 表明如果参数满足特定条件 a==2b-c，那么方程组有解：
对于非线性方程，解的存在性可能是非常复杂的.
一个非常简单的二元非线性方程组：
Solve 显示该方程组没有一般解：
Reduce 给出解存在的完全条件：
消去变量
在 Wolfram 语言中，写出一组联立方程，也就是指定变量之间的约束集合. 使用 Solve，就是在方程的约束下，求一些变量用其他变量表示的值.
Solve[eqns,vars,elims]
关于 vars 求解，消去变量 elims
Eliminate[eqns,elims]
整理方程消去变量 elims
消去变量.
两个包含 x，y 及“参数” a 和 b 的方程：
如果关于 x 和 y 求解，将得到用 a 和 b 表示的结果：
类似地，如果关于 x 和 a 求解，将得到用 y 和 b 表示的结果：
但是，如果只关于 x 求解，就必须指定消去 y 还是 a 或 b. 此处消去 y，则得到用 a 和 b 表示的结果：
如果消去 a，则得到用 y 和 b 表示的结果：
有时，用户可能想明显地构造变量已被消去的方程，使用 Eliminate 可以做到这一点.
通过消去变量 a，合并 eqn 中的两个方程：
消去 y 而不是 a 得到的结果：
作为 Eliminate 的更复杂的例子，考虑将 用“对称多项式” 和 表示的问题.
要解决这个问题，必须用 a 和 b 表示 f，而消去原来的变量 x 和 y：
在处理方程组时，常常把某些对象作为真“变量”，另一些作为“参数”. 在某些情况下，用户可能需要知道对什么参数值，变量之间的特定关系总能 满足.
SolveAlways[eqns,vars]
求对 vars 的所有值 eqns 都被满足的参数值
求解使关系式总成立的参数.
求解对于所有 x，方程都成立的参数值：
使两个级数相等：
求解待定系数的值：
关系运算符和逻辑运算符
x==y
等于（也输入为 xy）
x!=y
不等于（也输入为 x≠y）
x>y
大于
x>=y
大于等于（也输入为 x≥y）
x<y
小于
x<=y
小于等于（也输入为 x≤y）
x==y==z
全相等
x!=y!=z
互不相等（不同）
x>y>z
，etc.
严格递减，等等.
关系运算符.
检验是否 10 小于 7. 结果为 False：
这些数并非全不相等，故结果为 False：
同时使用 < 和 <=：
因为这两个量都是数值，故 Wolfram 语言能确定此不等式为真：
Wolfram 语言无法确定此不等式是真还是假：
!p
非（也输入为 ¬p）
p&&q&&…
与（也输入为 p∧q∧…）
p||q||…
或（也输入为 p∨q∨…）
Xor[p,q,…]
异或（也输入为 p⊻q⊻…）
Nand[p,q,…]
and
Nor[p,q,…]
与非和或非（也输入为 ⊼ 和 ⊽）
If[p,then,else]
如果 p 为 True，给出 then，如果 p 为 False，给出 else
LogicalExpand[expr]
展开逻辑表达式
逻辑运算符.
两个检验都为 True，故与的结果为 True：
应当记住逻辑运算符 ==、&& 和 || 在 Wolfram 语言中都是双字符. 如果你使用过编程语言比如C语言，你会发现这个表示法很熟悉，其与C语言是相同的.
Wolfram 语言不知道这是真还是假：
Wolfram 语言把此表达式原样给出：
使用 LogicalExpand 展开这些项：
求解逻辑组合的方程组
给 Solve 一个方程列表时，假定用户想使所有的方程同时被满足. 也可以给 Solve 更复杂的方程的逻辑组合.
Solve 假定方程 x+y==1 和 x-y==2 同时成立：
上式的另一种形式，使用逻辑连接符 &&：
指定 x+y==1 或者 x-y==2. Solve 给出相应于两个可能性的 x 的两个解：
Solve 给出这个方程的三个解：
如果明确包括 x!=0，则其中一个解被排除：
这是稍微复杂一些的例子. 注意 || 的优先级低于 &&，故方程应解释为 (x^3==x&&x!=1)||x^2==2，而不是 x^3==x&&(x!=1||x^2==2)：
使用 Solve 所得的最终结果是变换规则的形式. 而使用 Reduce 或 Eliminate，那么结果是能进一步处理的逻辑语句.
给出代表方程 x^2==x 的解的逻辑语句：
求满足 x^5==x 但不是 x^2==x 的解的 x 值：
由 Reduce 生成的逻辑语句能看作是方程解集合的表示. 逻辑连接符 &&，|| 等则是相应于解集的运算.
eqns1||eqns2
解集的并
eqns1&&eqns2
解集的交
!eqns
解集的补
Implies[eqns1,eqns2]
eqns1 中包含 eqns2 的部分
关于解集的运算.
正如 "算符" 中讨论的，我们经常会发现对逻辑连接符使用特殊表示法往往是方便的.
输入使用 Implies 和 Or 的特殊表示法：
不等式
正如方程 x^2+3x==2 所声明的 x^2+3x 等于2，因此不等式 x^2+3x>2 声明 x^2+3x 大于2. 在 Wolfram 语言中，Reduce 不仅适用于方程，也适用于不等式.
Reduce[{ineq1,ineq2,…},x]
化简关于 x 的不等式集合
多变量不等式的操作.
把一对不等式化简为一个不等式：
不等式不可能同时得到满足：
当应用于方程时，Reduce[eqn,x] 试图获得由x 的形式 x==r1，… 的简单方程组组成的结果. 而当应用于不等式时，Reduce[ineq,x] 做完全类似的事情，并试图获得由 x 的形式为 l1<x<r1，… 的简单不等式组成的结果.
把二次方程化简为 x 的两个简单方程：
把二次不等式化简为 x 的两个简单不等式：
由 Reduce[ineq,x] 产生的结果可以用来代表由不等式描述的一系列区间. 由于 次多项式的图示可以上下起伏多达 次， 次多项不等式可以产生多达 个不同区间.
不等式产生三个不同区间：
区间的两端为根和极点：
求解该不等式需要引入 ProductLog：
超越函数如 的图示上下起伏无穷多次，所以可以生成无穷多区间.
第二个不等式只允许有限多的区间：
这个例子表明 Reduce 如何代表无穷多的区间：
相当简单的输入可能产生较为复杂的结果：
如果有包含 <= 和 < 的不等式，就可能有满足不等式的孤立点. Reduce 通过给出方程代表这样的点.
该不等式只能在两个孤立点满足：
产生区间和孤立点：
Reduce[{ineq1,ineq2,…},{x1
，
x2
，… }]
化简由一些变量组成的不等式集合
多变量不等式.
对于包含多个变量的不等式，Reduce 产生具体区间的嵌套集合，这里后来的变量具有依赖于前面变量的边界.
使用 x 和 y 的嵌套不等式代表单位园板：
从几何上看，任何线性不等式把空间分为两半. 因此，线性不等式的列表定义了多面体，有时候是有界的，有时候不是. Reduce 用嵌套不等式表示这样的多面体. 多面体的角总是出现在这些不等式的终端.
在平面上定义一个三角区域：
即使是一个单一的三角形也可能需要使用两部分描述：
一般来说，不等式列表表示几何对象互相重叠的区域. 通常这些描述可以相当复杂.
这里代表单位园板在线一侧的部分：
两个园板的交集：
如果园板距离太远，则没有交集：
下面是涉及超越不等式的例子：
如果有包含参数的不等式，Reduce 自动处理可能出现的不同情况，正如其对方程的处理一样.
区间的形式取决于 a 的值：
取决于 a 的值，可以得到双曲线或椭圆区域：
Reduce 试图提供由不等式集合定义的区域的完整描述. 然而，有时候，用户可能只想找到满足不等式的变量值的个别例子. 可以使用 FindInstance 做到这一点.
FindInstance[ineqs,{x1,x2,…}]
试图寻找满足 ineqs 的 xi 的例子
FindInstance[ineqs,vars,n]
试图寻找 n 个例子
寻找满足不等式的个别点.
寻找满足不等式的具体实例：
没有任何办法可以满足不等式.
FindInstance 在一定程度上类似于用于方程的 Solve 的不等式. 类似于 Solve，返回一个给出变量具体值的规则列表. 但是，尽管对于方程，这些值可以笼统地给出所有解的准确表示，然而，对于不等式，只能对应于由不等式所描述的区域内的孤立样本点.
每次使用具体输入调用 FindInstance，将给出同样的输出. 并且当我们有对应于有些特殊或局限性的点的实例，将优先返回这些输出. 但一般而言，由 FindInstance 返回的实例的分布通常看起来有点随机. 然而，每个实例实际上建设性地证明了用户所提供的不等式是可以被满足的.
如果要求单位园板中的一点，FindInstance 给出原点：
在单位园板中找到500个点：
这些点的分布看起来比较随机：
不同域上的方程和不等式
Wolfram 语言通常假定方程中出现的变量可以代表任意复数. 但是当用户使用 Reduce 时，可以明确地告诉 Wolfram 语言变量表示更严格的域中的对象.
Reduce[expr,vars,dom]
在域 dom 上化简 eqns
Complexes
复数
Reals
实数
Integers
整数
不同域上的求解方法.
Reduce 默认情况下假定 x 可以是复数，并且给出所有5个复数解：
假定 x 是实数，并且只给出实数解：
假定 x 是整数，并且只给出整数解：
单变量的单个多项式方程的解集总是离散解的有限集合. 并且在这样的情况下，用户可以通过选择位于域 dom 中的解，把 Reduce[eqns,vars,dom] 用来过滤解.
但是一旦我们有更多的变量时，情况就变得更复杂了，我们就有了对应于参数曲线或表面的方程的解，但是对这些参数曲线或表面来说，一些变量的值可以依赖于其他变量的值. 通常，这种依赖性可以使用方程或不等式的集合来描述，但是当我们从一种域到另一种域时，这种依赖的形式可能发生显著的变化.
把复数上的解作为单个公式给出：
为了表示实数上的解，需要引入不等式：
在整数范围内，解可以表示为离散点的方程：
如果用户只输入方程，那么 Reduce 将默认地假定所有变量都是复数. 但是如果用户的输入只涉及不等式，那么 Reduce 将假定所出现的任何代数变量都是实数，由于不等式只能对实数大小进行比较.
由于这是不等式中出现的变量，故而假定他们是实数：
Complexes
polynomial!=0，xi==Root[…]
Reals
Root[…]<xi<Root[…]，xi==Root[…]
Integers
任意复杂
多项式方程和不等式的解的概要块元件.
对于实数和复数域上的多项式系统，解总是由一些有限数目的部分组成，在这些组成部分中，变量的值由代数数或者函数给出.
组成部分由 x 上的方程和不等式区分：
组成部分由 x 上的不等式区分：
虽然原则上 Reduce 总是可以对具有实变量或复数变量的多项式方程和不等式找到完整的解，由于组成部分的数目通常在变量数目增加的时候呈指数增长，所有结果经常是很复杂的.
在3个变量的情况下，这里的解已经包括8个组成部分：
一旦用户引入函数如 Sin 或者 Exp，即使是单个实变量或复数变量的方程也能有具有有限数目的组成部分的解. Reduce 通过引入其他额外的参数对这些组成部分加标签. 但是默认情况下，在一个给定的解中，第 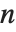个参数被命名为C[n]. 一般情况下，用户可以通过给出选项设置 GeneratedParameters->f 指明他应该被命名为 f[n].
组成部分使用整数参数 c1 加标签：
Reduce 不仅可以处理实数变量和复数变量的方程，也能够处理整数变量的方程. 求解这样的 Diophantine equations 经常可能是很困难的问题.
描述在实数域上方程的解是很直接的：
整数域上的解涉及 8 的约数：
求解这样的方程需要对很大的数目求因子：
Reduce 可以在整数域上求解任意线性方程或不等式系统. 在具有 个变量的 个线性方程的情况下，通常需要引入 个参数. 但是在不等式的情况下，可能需要引入更多更多的参数.
需要3个参数，即使我们只有2个变量：
在两个变量的情况下，Reduce 可以在整数域上求解任何二次方程. 结果可以是形如 Fibonacci 的序列，由二次无理数的幂表示.
一个 Pell 方程的解：
特定的 C[1] 的实际值是整数，正如他们本应该是的一样：
Reduce 可以处理整数域上的许多特殊的方程类别.
Reduce 对一个 Thue 方程求解：
把右边的值改为 3，现在方程无解：
有时候，在整数域上的方程具有相当随机的解集. 并且甚至是方程上微小的改变也经常导致无解的情况出现.
对于在实数和复数域上的多项式方程，我们具有一个确定的决策过程（ decision procedure ）来决定是否有解存在. 但是对于整数域上的多项式方程，Hilbert’s tenth 问题的无解性表明不可能有这样的普遍适用的过程.
然而，对于一些专门类别的方程，我们可以找到这样的过程，事实上，许多这样的过程在 Reduce 中得到实现. 但是处理不同类别的方程可能经常需要使用数论的所有不同分支，而且也需要许多不同类别的计算. 事实上，我们称之为普遍 （ universal ）整数多项式方程，在这种情况下，输入一些变量可以使其他变量的解对应于任何可能程序的输出. 这意味着对于这样的方程，一般不可能从固定元素，如代数函数，建立任何闭集解.
如果包含函数如 Sin，那么即使对涉及实数和复数的方程，也可能出现同样的问题.
Reduce 有效地在整数范围内求解一个方程：
Reduce[eqns,vars,Modulus->n]
寻找 modulo n 的解
处理涉及整数 modulo n 的方程.
由于对整数方程 modulo n 只有有限的可能解，Reduce 可以系统地找到他们.
寻找所有 modulo 4 的解：
Reduce 也可以处理涉及几个不同 moduli 的方程.
涉及两个不同的 moduli 的方程：
Reduce[expr,vars,dom]
对所有变量指定一个默认域
Reduce[{expr1,…,x1∈dom1,…},vars]
对变量明确指明单个域
对变量指定不同域的方法.
假定 x 是一个整数，但是 y 是一个实数：
Reduce 通常把复数变量作为单个对象处理. 但是在处理不是解析或具有分支的函数时，有时候必须把他们分成实变量Re[z] 和虚变量 Im[z] 的对.
结果涉及不同的实部和虚部：
在虚部上具有不同的条件：
默认情况下，Reduce 假定在不等式中以代数形式出现的变量是实数. 但是用户可以通过把 Complexes 明确指明为默认域来进行重载. 在这种情况下，能够指明某些变量仍然是实数经常是有用的.
Reduce 默认情况下假定 x 是实数：
迫使 Reduce 考虑当 x 可以是复数的情况：
由于 x 没有以代数形式出现，Reduce 马上假定他可以是复数：
x 是一个实数，但是 y 可以是复数：
FindInstance[expr,{x1,x2,…},dom]
试图寻找在 dom 中满足 expr 的 xi 的一个实例
FindInstance[expr,vars,dom,n]
试图寻找 n 个实例
Complexes
复数域
Reals
实数域
Integers
整数域
Booleans
布尔域 （True 和 False）
在不同域中寻找特定解.
Reduce 总是返回等式或不等式组的解的完整表示. 然而，有时候，用户可能只想要寻找特定的样本解. 这可以通过使用 FindInstance 来实现.
如果 FindInstance[expr,vars,dom] 返回 {}，那么这意味着 Wolfram 语言可以有效地证明 expr 不能被特定域内的变量值所满足. 当 expr 可以被满足的时候，FindInstance 通常将任意选择值来实现，如 "不等式" 中关于不等式的讨论.
尤其对于整数方程，即使当 Reduce 不能找到完整解的时候，FindInstance 也经常可以找到方程的解. 在这样的情况下，他通常返回方程的最小解之一.
在一个椭圆曲线上寻找最小整数点：
FindInstance 的一个特征是对于变量为 True 或 False 的布尔表达式也适用. 可以使用 FindInstance 来决定一个特定的表达式是否是可满足的，因此对于可使表达式为 True 的这些变量的真值，具有一些选择.
该表达式不能对任意 p 和 q 满足：
但以下表达式可以做到：
解集的表示法
方程或不等式的任意组合可以被明确定义为某种空间的一个区域. 基本函数 Reduce 把这种类型的隐式描述转化为显式描述.
关于方程或不等式的隐式描述是足够的，如果用户只是想要测试由变量值指定的一个点是否位于区域内. 但是为了理解区域的结构，或者产生区域内的点，用户通常需要一个更明确的描述，如从 Reduce 中获得的一样.
不等式明确定义了一个半圆区域：
显示点 位于区域内：
Reduce 给出区域更明确的表示法：
如果对 x 选出和第一个不等式一致的值，那么我们马上获得 y 的明确不等式：
Reduce[expr,{x1,x2,…}] 被设置用来描述区域，具体方法如下：首先给出对 x1 的固定条件，然后给出取决于 x1 的 x2 的条件，接下来是取决于 x1 和 x2 的 x3 的条件，以此类推. 该结构具有特征，允许用户通过连续对每个 xi 依次选值来挑选点—与当用户在函数如 Table 中使用迭代方法很相似.
给出区域的表示法，在该区域内用户首先选出 y 的值，然后是 x 的值：
在一些简单的情况下，由方程或不等式系统定义的区域将最终只有一个组成部分. 在这样的情况下，从 Reduce 得到的输出将具有形式 e1&&e2…，其中每个 ei 是一个涉及变量 xi 的方程或不等式.
然而，在大部分情况下，将有几个组成部分，由包含形式如 u1||u2||… 的输出表示. Reduce 通常试图最小化用来描述区域的组成部分的数量. 但是在一些情况下，可能需要多参数化来覆盖单个连接的组成部分，其中每个部分都将作为 Reduce 的输出中的不同部分出现.
在表示解集时，通常寻找一些可以使用如 …&&(u1||u2)&&… 的形式描述的组成部分. 默认情况下，Reduce 这样做以使得返回结果尽可能的紧凑. 用户可以使用 LogicalExpand 来产生一个展开形式，其中每个组成部分分隔出现.
在产生最紧凑结果的过程中，有时候 Reduce 最终使后来的变量 xi 的条件更多取决于前面的 xi，然而这并不是严格必须的. 用户可以通过设置选项 BacksubstitutionTrue. 迫使 Reduce 产生特定 xi 只对前面的 xi 有最小依赖性的结果. 通常这将导致相当大的输出，虽然对结果可能更容易解释.
默认情况下，Reduce 表示 y 关于 x 的条件：
回代法允许给出 y 的条件，而不涉及 x：
CylindricalDecomposition[expr,{x1,x2,…}]
产生由 expr 定义的区域的柱形代数分解
GenericCylindricalDecomposition[expr,{x1,x2,…}]
寻找由 expr 定义区域的分解的完全维度部分，以及区域剩余部分的超曲面
SemialgebraicComponentInstances[expr,{x1,x2,…}]
给出每个由 expr 定义区域的连接部分中的至少一个点
柱形代数分解.
对于实数上的多项式方程或不等式，由 Reduce 返回的结果的结构通常是柱形代数分解 （cylindrical algebraic decomposition ）或 CAD. 有时候 Reduce 可以产生更简单的形式. 但是在所有情况下，用户可以通过使用CylindricalDecomposition 获得完整的CAD. 对于只包含不等式的系统， GenericCylindricalDecomposition 给出“大部分”解集，并且通常更快.
由抛物线定界的区域的柱形代数分解：
给出沿着包含边界的曲线的解集的二维组成部分：
从解集的两个组成部分寻找解：
该解包含解集的每个组成部分的一些点：
量词
在一个如 x^4+x^2>0 的语句中，Wolfram 语言把变量 x 当作具有确定但是未指定的值来处理. 然而，有时候，提供 x 的可能值集合的语句是有用的. 可以使用量词来实现这个功能.
ForAll[x,expr]
expr 对 x 所有值成立
ForAll[{x1,x2,…},expr]expr
对所有 xi 的所有值成立
xi
ForAll[{x1,x2,…},cond,expr]expr
对所有满足 cond
的 xi 成立
Exists[x,expr]
存在 x 的值使得 expr 成立
Exists[{x1,x2,…},expr]
存在 xi 的值使得 expr 成立
Exists[{x1,…},cond,expr]
存在 xi 的值满足 cond 并使得 expr 成立
量词的结构.
用户可以在 Wolfram 语言中像使用方程、不等式或逻辑语句一样经常地使用量词. 在绝大多数情况下，量词将不会因为计算立即被改变. 但是可以通过函数如 FullSimplify 和 Reduce 简化或消去.
声明存在一个 x 使得不等式成立. 这里的输出就是输入的一个格式化版本：
FullSimplify 验证了该声明为真：
给出 False，因为当 x 等于零时，不等式不成立：
Wolfram 语言支持在谓词逻辑和纯数学中使用的量词的标准记号版本. 可以输入 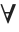作为 \[ForAll] 或者 EscfaEsc，并且可以输入 作为 \[Exists] 或者 EscexEsc. 然而，为了使得记号更为精确，Wolfram 语言使量化的变量作为一个下标. 变量所满足的条件也可以在下标中提供，使用逗号分隔.
∀xexprForAll[x,expr]
∀{x1,x2,…}exprForAll[{x1,x2,…},expr]
∀x,condexprForAll[x,cond,expr]
∃xexprExists[x,expr]
∃{x1,x2,…}exprExists[{x1,x2,…},expr]
∃x,condexprExists[x,cond,expr]
量词记号.
给定一个包含量词的语句，有一些可能将其求解为可以消去量词的相当语句的重要例子. 与求解一个方程类似，这样的量词消去法把关于对所有 x 或一些 x 什么为真的明确语句转化为关于条件成立的明确语句.
Resolve[expr]
试图从 expr 中消去量词
Resolve[expr,dom]
试图消去量词，其中假定所有变量都在域 dom 中
消去量词.
显示存在一个 x 使得方程为真：
显示只有当 c 遵循某个条件，方程才能成立：
Resolve 可以总是在复数范围内的多项式等式和不等式集合，以及实数范围内的多项式等式和不等式集合中消去量词. 其也可以从布尔表达式中消去量词.
寻找使得在实数范围内二次项为正的条件：
显示有一种办法可以对 p 和 q 赋予真值，从而使得表达式为真：
也可以以 Reduce 的方式使用量词. 如果用户给 Reduce 提供了一个等式或者不等式的集合，那么他将会试图产生完整解集的具体表示. 但是有时候，用户可能想要表示一个更为全局的问题，比如，解集是否包含 x 的所有值，或者是否不包含任何值. 量词给我们提供了指明这些问题的方便的途径.
给出解集的完整结构：
给出一个解存在的条件：
对于大量数学问题都可能可以使用量词表示成数学公式.
寻找使得一个圆包含在任意圆锥体内的条件：
寻找一条线与一个圆相交的条件：
定义 q 为一般的首一四次多项式：
寻找使得四次多项式相等的所有根对的条件：
虽然在整数上消去量词在计算上是不可能的问题，然而 Wolfram 语言在特殊情况下可以实现这个功能.
显示 不可能是一个有理数：
但 是一个有理数：
最小化和最大化
Minimize[expr,{x1,x2,…}]
最小化 expr
Minimize[{expr,cons},{x1,x2,…}]
最小化 expr，约束条件为 cons
Maximize[expr,{x1,x2,…}]
最大化 expr
Maximize[{expr,cons},{x1,x2,…}]
最大化 expr，约束条件为 cons
最小化和最大化
Minimize 和 Maximize 产生在最小值或最大值处获得的值以及指明最小值或最大值出现规则的列表.
寻找二次函数的最小值：
对 x 应用规则给出最小值处的值：
关于 x 和 y 进行最大化：
Minimize[expr,x] 最小化 expr，并允许 x 位于从 到 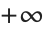的所有可能值范围内. Minimize[{expr,cons},x] 最小化 expr，并满足约束条件 cons. 约束条件可以包括等式和不等式的任意组合.
寻找最小值，约束条件为 ：
在单位圆内寻找最大值：
在椭圆内寻找最大值. 结果相当复杂：
沿着一条线寻找最大值：
Minimize 和 Maximize 能够求解任何线性规划问题，其中目标函数 expr 和约束条件 cons 只包含线性组成的变量 .
一个典型的线性规划问题：
原则上，他们也可以求解任何多项式规划问题，其中目标函数和约束条件包含由变量组成的任意多项式函数. 有许多重要的几何或其他问题可以用这个方法构建.
求解最大化矩形面积的简单几何问题，约束条件为固定的周长：
寻找在单位球体内的立方体的最大容积：
Minimize 和 Maximize 的一个重要特征是他们总是寻找全局最小值和最大值. 通常，函数会有不同的局部极小值和极大值，在该处梯度为零. 但是 Minimize 和 Maximize 使用全局方法寻找绝对最小值和最大值，而非局部极值.
一个具有多个局部最大值和最小值的函数：
Maximize 寻找全局最大值：
如果给出无界函数，Minimize 和 Maximize 将返回 和 作为最小值和最大值. 如果用户给的约束条件永远不能满足，他们将返回 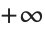和 作为最小值和最大值，并且 Indeterminate 作为变量值.
Minimize 和 Maximize 的精妙之处是允许不严格的不等式 和严格不等式 . 在不严格不等式的情况下，最小值或最大值恰好位于边界 是没有问题的. 但是如果在严格不等式的情况下，原则上，一个最小值或最大值必须至少无限位于边界以内.
在严格不等式情况下，Wolfram 语言显示一个警告信息，并返回边界上的点：
Minimize 和 Maximize 一般假设给出的所有变量都是实数. 但是通过给出一个约束条件如 x∈Integers 我们可以指明该变量实际上应该是一个整数.
只在 x 和 y 的整数范围内进行最大化：
Minimize 和 Maximize 可以在一个有界多边形的整数范围内计算最大值和最小值. 我们称之为整数线性规划.
在一个三角形范围内关于 x 和 y 的整数值进行最大化：
Minimize 和 Maximize 可以对具有参数的多项式优化产生精确的结果.
寻找一个一般二次多项式的最小值：
MinValue[{f,cons},{x,y,…}]
给出 f 的最小值，约束条件为 cons
MaxValue[{f,cons},{x,y,…}]
给出 f 的最大值，约束条件为 cons
ArgMin[{f,cons},{x,y,…}]
给出 f 在约束条件 cons 下被最小化的位置
ArgMax[{f,cons},{x,y,…}]
给出 f 在约束条件 cons 下被最大化的位置
计算最小值和最大值的值和位置
Maximize 给出最大值的值和位置：
如果只需要最大值，则使用 MaxValue：
对于严格的多项式不等式约束，只计算最大值可能会更快：
ArgMax 给出取得最大值的位置：