WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター
リストの操作

リストの操作

リストの構築リストの分割と充填
指標によるリストの操作疎な（スパース）配列：リストの操作
ネストしたリスト
リストの構築
リストはWolfram言語で広く使われており，構築方法もたくさんある．
Range[n]
リスト {1,2,3,…,n}
Table[expr,{i,n}]
i が1から n までの expr の値
Array[f,n]
リスト {f[1],f[2],…,f[n]}
NestList[f,x,n]
最大 n までネストする {x,f[x],f[f[x]],…}
Normal[SparseArray[{i1->v1,…},n]]
要素 ik が vk である長さ n のリスト
Apply[List,f[e1,e2,…]]
リスト {e1,e2,…}
明示的なリストの構築方法
これは2の最初の5つのベキ乗の表を与える：
Wolfram Language code: Table[2 ^ i, {i, 5}]
こうしても同じ結果が得られる：
Wolfram Language code: Array[2 ^ #&, 5]
これも同じようなリストになる：
Wolfram Language code: NestList[2#&, 1, 5]
SparseArrayを使うと，特定の位置における値が指定できる：
Wolfram Language code: Normal[SparseArray[{3 -> x, 4 -> y}, 5]]
値の指定にはパターンを使うこともできる：
Wolfram Language code: Normal[SparseArray[{i_ -> 2 ^ i}, 5]]
あらかじめリストの長さがどのくらいになるべきか，また各要素をどのように生成すべきかが分かることがしばしばある．さらに，ひとつのリストから別のリストが得られることもある．
Table[expr,{i,list}]
i が list からの値を取る expr の値
Map[f,list]
list の各要素に f を適用する
MapIndexed[f,list]
i 番目の要素に f[elem,{i}]を与える
Cases[list,form]
form と一致する list の要素を与える
Select[list,test]
test[elem]がTrueである要素を選び出す
Pick[list,sel,form]
list 中の要素で，それに対応する sel の要素が form にマッチするものを拾い出す
TakeWhile[list,test]
test[ei]がTrueである限りにおいて，list の最初から要素 ei を与える
list[[{i1,i2,…}]]
または
Part[list,{i1,i2,…}]
list の指定された部分のリストを与える
他のリストからのリストの構築
これは5よりも小さい要素を選び出す：
Wolfram Language code: Select[{1, 3, 7, 4, 10, 2}, # < 5&]
最初に5以上の要素に遭遇するまでの要素を取り出す：
Wolfram Language code: TakeWhile[{1, 3, 7, 4, 10, 2}, # < 5&]
これは指定の番号の部分を明示的に与える：
Wolfram Language code: {a, b, c, d}[[{2, 1, 4}]]
これは2番目のリスト中で1で示されている要素を抽出する：
Wolfram Language code: Pick[{a, b, c, d}, {1, 0, 1, 1}, 1]
プログラムの実行中，結果のリストを蓄積したいこともあるだろう．その際はSowとReapを使うとよい．
Sow[val]
値 val を，囲っている最も近くのReapに播く
Reap[expr]
expr を評価し，Sowで播かれたリストの値も一緒に返す
SowとReapを使う
このプログラムは数値を反復的に2乗する：
Wolfram Language code: Nest[# ^ 2&, 2, 6]
これも同じ計算をするが，1000より大きい途中結果を蓄積したリストを作る：
Wolfram Language code: Reap[Nest[(If[# > 1000, Sow[#]];# ^ 2)&, 2, 6]]
あまり効果的ではないがこれに代る方法として，一時的な変数を導入して t={}から始め，連続的にAppendTo[t,elem]を使うというものがある．
指標によるリストの操作
Part[list,spec]
または
list[[spec]]
リストの部分
Part[list,spec1,spec2,…]
または
list[[spec1,spec2,…]]
ネストしたリストの部分
n
最初から n 番目の部分
-n
最後から n 番目の部分
{i1,i2,…}
部分のリスト
m;;n
m から n までの部分
All
部分すべて
リストの部分の抽出
これは部分1と3のリストを与える：
Wolfram Language code: {a, b, c, d}[[{1, 3}]]
これはネストしたリストである：
Wolfram Language code: m = {{a, b, c}, {d, e}, {f, g, h}};
これは最初と3番目の部分のリストを与える：
Wolfram Language code: m[[{1, 3}]]
これはこれらそれぞれの最初の部分のリストを与える：
Wolfram Language code: m[[{1, 3}, 1]]
これは最初の2つの部分のリストを与える：
Wolfram Language code: m[[{1, 3}, {1, 2}]]
mの最初の2つの部分を与える：
Wolfram Language code: m[[1 ;; 2]]
それぞれの最後の部分を与える：
Wolfram Language code: m[[1 ;; 2, -1]]
これはすべてのサブリストの2番目の部分を与える：
Wolfram Language code: m[[All, 2]]
すべてのサブリストの最後の2つの部分を与える：
Wolfram Language code: m[[All, -2 ;; -1]]
m[[…]]=value のような割当てを使うとリストの一部をいつでも再設定することができる．
これはmの部分1，2を再設定する：
Wolfram Language code: m[[1, 2]] = x
これによりmの形はこうなった：
Wolfram Language code: m
これは部分1をxに，部分3をyに再設定する：
Wolfram Language code: m[[{1, 3}]] = {x, y};m
これは部分1と3の両方をpに再設定する：
Wolfram Language code: m[[{1, 3}]] = p;m
これはmのもとの形を回復する：
Wolfram Language code: m = {{a, b, c}, {d, e}, {f, g, h}};
これは，m[[{1,3},{1,2}]]で指定したすべての部分を再設定する：
Wolfram Language code: m[[{1, 3}, {1, 2}]] = x;m
;;を用いて指定範囲のすべての指標を示すことができる：
Wolfram Language code: m[[1 ;; 3, 2]] = y;m
ネストしたリストを，全体が空間に置かれている各要素は座標の指標で与えられた位置にある，と考えると便利なことがある．このように考えると list[[spec1,spec2,…]]を直接幾何学的に解釈できるようになる．speck が単一の整数なら，それは k 番目の次元の単一スライスを抽出することを表し，これがリストの場合は平行スライスのリストを抽出することを表す．list[[spec1,spec2,…]]の最終結果は連続する次元をスライスして取得した要素の集合になる．
これは二次元配列として置かれたネストしたリストである：
Wolfram Language code: (m = {{a, b, c}, {d, e, f}, {g, h, i}})//TableForm
行1および3を，次いで列1および2を取り出す：
Wolfram Language code: m[[{1, 3}, {1, 2}]]//TableForm
Partはネストしたリストの構造化されたスライスを取り出しやすいように設定されている．しかし，場合によっては個々の部分の任意の集合を取り出したいこともあるだろう．そのような場合はExtractを使うとよい．
Part[list,{i1,i2,…}]
リスト{list[[i1]],list[[i2]],…}
Extract[list,{i1,i2,…}]
要素 list[[i1,i2,…]]
Part[list,spec1,spec2,…]
連続スライスによって指定された部分
Extract[list,{{i1,i2,…},{j1,j2,…},…}]
個々の部分のリスト{list[[i1,i2,…]],list[[j1,j2,…]],…}
スライスの取得と個々の部分の取得
これは個々の部分1,3と1,2を抽出する：
Wolfram Language code: Extract[m, {{1, 3}, {1, 2}}]
Extractの重要な機能に，Positionのような関数で返されるのと同じ形の部分の位置のリストを取るというものがある．
これはネストしたリストを設定する：
Wolfram Language code: m = {{a[1], a[2], b[1]}, {b[2], c[1]}, {{b[3]}}};
これはmにおける位置のリストを与える：
Wolfram Language code: Position[m, b[_]]
これはそれらの位置にある要素を抽出する：
Wolfram Language code: Extract[m, %]
Take[list,spec]
リスト中の指定の部分を取り出す
Drop[list,spec]
リスト中の指定の部分を除く
Take[list,spec1,spec2,…]，Drop[list,spec1,spec2,…]
ネストしたリストの各レベルにおける指定部分を取り出したり除いたりする
n
最初の n 個の要素
-n
最後の n 個の要素
{n}
要素 n のみ
{m,n}
m 番目から n 番目までの要素（両要素を含む）
{m,n,s}
m 番目から n 番目までの要素刻み幅 s で
All
全部の部分
None
何も取り出さない
リスト中の連続する要素の抽出と除去
これは位置2から始めて1つ置きの要素を取り出す：
Wolfram Language code: Take[{a, b, c, d, e, f, g}, {2, -1, 2}]
これは1つ置きの要素を除去する：
Wolfram Language code: Drop[{a, b, c, d, e, f, g}, {2, -1, 2}]
Partと同じようにTakeやDropもネストしたリストの連続したレベルで一連のスライスを取り出すと見ることができる．TakeやDropを使って配列における要素のブロックを扱うこともできる．
これは3×3配列である：
Wolfram Language code: (m = {{a, b, c}, {d, e, f}, {g, h, i}})//TableForm
これは最初の2×2の部分配列である：
Wolfram Language code: Take[m, 2, 2]//TableForm
これは最初の2列の全要素を取り出す：
Wolfram Language code: Take[m, All, 2]//TableForm
これは最初の2列の要素はひとつも残さない：
Wolfram Language code: Drop[m, None, 2]//TableForm
Prepend[list,elem]
list の頭に element を加える
Append[list,elem]
list の末尾に element を加える
Insert[list,elem,i]
位置 i に element を挿入する
Insert[list,elem,{i,j,…}]
位置{i,j,…}に挿入する
Delete[list,i]
位置 i の要素を除去する
Delete[list,{i,j,…}]
位置{i,j,…}の要素を除去する
リストへの要素の挿入とリストからの要素の除去
これはリスト中の要素2，1をxにする：
Wolfram Language code: Insert[{{a, b, c}, {d, e}}, x, {2, 1}]
これで再び要素を削除する：
Wolfram Language code: Delete[%, {2, 1}]
ReplacePart[list,i->new]
list の位置 i の要素を new で置換する
ReplacePart[list,{i,j,…}->new]
list[[i,j,…]]を new で置換する
ReplacePart[list,{i1->new1,i2->new2,…}]
位置 in の部分を newnで置換する
ReplacePart[list,{{i1,j1,…}->new1,…}]
位置{in,jn,…}の部分を newnで置換する
ReplacePart[list,{{i1,j1,…},…}->new]
すべての部分 list[[ik,jk,…]]を new で置換する
リストの部分の置き換え
これはリストの3番目の要素をxで置換する：
Wolfram Language code: ReplacePart[{a, b, c, d}, 3 -> x]
これはリストの最初と4番目の部分を置換する．複数の部分の指定には二重リストが必要である：
Wolfram Language code: ReplacePart[{a, b, c, d}, {{1}, {4}} -> x]
これは3×3単位行列である：
Wolfram Language code: IdentityMatrix[3]
これは行列の2，2要素をxで置換する：
Wolfram Language code: ReplacePart[%, {2, 2} -> x]
ReplacePartは常に新しいリストを生成するということを理解しておかなければならない．これは m[[…]]=val が行うように，すでにシンボルに割り当てられたリストを変更したりはしない．
値のリストをalistに割り当てる：
Wolfram Language code: alist = {a, b, c, d}
第3要素がxで置換されたリストのコピーである：
Wolfram Language code: ReplacePart[alist, 3 -> x]
alistの値は変わっていない：
Wolfram Language code: alist
ネストしたリスト
{list1,list2,…}
リストのリスト
Table[expr,{i,m},{j,n},…]
expr の値の m×n×…表
Array[f,{m,n,…}]
値 f[i,j,…]の m×n×…配列
Normal[SparseArray[{{i1,j1,…}->v1,…},{m,n,…}]]
要素{is,js,…}が vs である m×n×…配列
Outer[f,list1,list2,…]
f で要素を結合した一般化された外積
Tuples[list,{m,n,…}]
list の要素の可能なすべての m×n×…配列
ネストしたリストの構築方法
これは2×3のネストしたリストに対応する表を生成する：
Wolfram Language code: Table[x ^ i + j, {i, 2}, {j, 3}]
これは上記と同じネストしたリストに対応する配列を生成する：
Wolfram Language code: Array[x ^ #1 + #2&, {2, 3}]
疎な配列において明示的に指定されていない要素は0であると解釈される：
Wolfram Language code: Normal[SparseArray[{{1, 3} -> 3 + x}, {2, 3}]]
最終リストの各要素は各入力リストからの1要素を含む：
Wolfram Language code: Outer[f, {a, b}, {c, d}]
Array，SparseArray，Outer等の関数は常に「完全配列」を生成する．完全配列では，特定レベルのすべてのサブリストがすべて同じ長さになる．
Dimensions[list]
完全配列の次元
ArrayQ[list]
指定されたレベルのすべてのサブリストが同じ長さかどうかテストする
ArrayDepth[list]
すべてのサブリストが同じ長さである深度
完全配列の関数
Wolfram言語は任意のネストしたリストを扱うことができる．リストが完全配列である必要はない．Tableを使って簡単に不調和配列を生成することができる．
これは三角配列を生成する：
Wolfram Language code: Table[x ^ i + j, {i, 3}, {j, i}]
Flatten[list]
list の全レベルを平坦化する
Flatten[list,n]
最上層から n 番目までのレベルを平坦化する
ArrayFlatten[list,rank]
配列の配列から平坦化した配列を作成する
サブリストと部分配列の平坦化
これは2×3の配列を生成する：
Wolfram Language code: Array[a, {2, 3}]
Flattenは事実上要素をその指標によって辞書式順序に並べる：
Wolfram Language code: Flatten[%]
これでブロック行列から行列が作られる：
Wolfram Language code: ArrayFlatten[{{{{1}}, {{2, 3}}}, {{{4}, {7}}, {{5, 6}, {8, 9}}}}]
Transpose[list]
list の最上層の2レベルを置き換える
Transpose[list,{n1,n2,…}]
list のレベル nk に k 番目のレベルを置く
ネストしたリストにおけるレベルの置き換え
次では2×2×2配列が作られる：
Wolfram Language code: Array[a, {2, 2, 2}]
レベル3がレベル1に現れるようにレベルを置換する：
Wolfram Language code: Transpose[%, {3, 1, 2}]
これで最初の配列を回復する：
Wolfram Language code: Transpose[%, {2, 3, 1}]
Map[f,list,{n}]
レベル n にある要素に f を写像する
Apply[f,list,{n}]
レベル n にある要素に f を適用する
MapIndexed[f,list,{n}]
レベル n の部分とその指標に f を写像する
ネストしたリストに関数を適用する
これはネストしたリストである：
Wolfram Language code: m = {{{a, b}, {c, d}}, {{e, f}, {g, h}, {i}}};
レベル2に関数fを写像する：
Wolfram Language code: Map[f, m, {2}]
レベル2に関数を適用する：
Wolfram Language code: Apply[f, m, {2}]
fを部分とその指標の両方に適用する：
Wolfram Language code: MapIndexed[f, m, {2}]
Partition[list,{n1,n2,…}]
n1×n1×…個のブロックに分割する
PadLeft[list,{n1,n2,…}]
n1×n1×…の配列を作るために左側に充填する
PadRight[list,{n1,n2,…}]
n1×n1×…の配列を作るために右側に充填する
RotateLeft[list,{n1,n2,…}]
レベル k で左側に位置 nk 分循環させる
RotateRight[list,{n1,n2,…}]
レベル k で右側に位置 nk 分循環させる
ネストしたリストの操作
これは，ネストしたリストである：
Wolfram Language code: m = {{{a, b, c}, {d, e}}, {{f, g}, {h}, {i}}};
各レベルで異なった量を循環させる：
Wolfram Language code: RotateLeft[m, {0, 1, -1}]
2×3×3配列を作るためにゼロで充填する：
Wolfram Language code: PadRight[%, {2, 3, 3}]
リストの分割と充填
Partition[list,n]
list を長さ n のサブリストに分割する
Partition[list,n,d]
オフセット d でサブリストに分割する
Split[list]
list を同一要素の組に分割する
Split[list,test]
test を満足する隣り合った要素に分割する
リスト要素の分割
これは3つずつのブロックに分割する：
Wolfram Language code: Partition[{a, b, c, d, e, f}, 3]
次はオフセット1で3つずつのブロックに分割する：
Wolfram Language code: Partition[{a, b, c, d, e, f}, 3, 1]
オフセットはブロックの大きさよりも大きくても構わない：
Wolfram Language code: Partition[{a, b, c, d, e, f}, 2, 3]
同一要素のグループに分割する：
Wolfram Language code: Split[{1, 4, 1, 1, 1, 2, 2, 3, 3}]
隣接する要素が同一ではないグループに分割する：
Wolfram Language code: Split[{1, 4, 1, 1, 1, 2, 2, 3, 3}, Unequal]
Partitionは事実上リストの連続する要素をサブリストに分ける．デフォルトではもとのリストから「はみ出す」サブリストは含まない．
これははみ出しが起る前に停止する：
Wolfram Language code: Partition[{a, b, c, d, e}, 2]
これもはみ出しが起る前に停止する：
Wolfram Language code: Partition[{a, b, c, d, e}, 3, 1]
Partitionを使ってもとのリストの端がはみ出すサブリストを含ませることもできる．デフォルトではもとのリストを循環的に使って追加要素を埋めていく．指定した要素で充填することも可能である．
これはもとのリストを循環的に扱った追加的なサブリストを含んでいる：
Wolfram Language code: Partition[{a, b, c, d, e}, 3, 1, {1, 1}]
もとのリストが要素xで充填されている：
Wolfram Language code: Partition[{a, b, c, d, e}, 3, 1, {1, 1}, x]
こうすると要素xとyを使って循環的に充填する：
Wolfram Language code: Partition[{a, b, c, d, e}, 3, 1, {1, 1}, {x, y}]
この場合は充填はせず，長さが違うサブリストが与えられる：
Wolfram Language code: Partition[{a, b, c, d, e}, 3, 1, {1, 1}, {}]
Partitionはテンプレートをもとのリストに沿ってスライドさせて要素を取り出すことでサブリストを抽出するものと考えることができる．このプロセスをどこから始めどこで終了するかをPartitionに指示することができる．
これはもとのリストと重なるすべてのサブリストを与える：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {-1, 1}, x]
こうすると最初の部分しか重ならない：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {-1, -1}, x]
Partition[list,n,d]
または
Partition[list,n,d,{1,-1}]
はみ出しのないサブリストだけを保存する
Partition[list,n,d,{1,1}]
最後の部分のはみ出しを許す
Partition[list,n,d,{-1,-1}]
最初の部分のはみ出しを許す
Partition[list,n,d,{-1,1}]
最初と最後のはみ出しを許す
Partition[list,n,d,{kL,kR}]
最初と最後のサブリストの並べ方を指定する
Partition[list,n,d,spec]
リスト list 中の要素を循環的に使って充填する
Partition[list,n,d,spec,x]
要素 x を繰り返し使って充填する
Partition[list,n,d,spec,{x1,x2,…}]
xi を循環的に繰り返して充填する
Partition[list,n,d,spec,{}]
充填は行わない
整列と充填の指定
整列指定{kL,kR}はPartitionに，もとのリストの最初の要素が最初のサブリストの位置 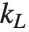にあり，もとのリストの最後の要素が最後のサブリストの 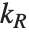の位置にある一連のサブリストを与えるように指示する．
aが最初のサブリストの位置1になるようにする：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {1, 1}, x]
aが最初のサブリストの位置2になるようにする：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {2, 1}, x]
aがまず位置4になる：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {4, 1}, x]
与えられたリストから循環的に充填する：
Wolfram Language code: Partition[{a, b, c, d}, 3, 1, {4, 1}, {x, y}]
ListConvolveのような関数は整列と充填にPartitionと同じ方法を使う．
場合によってはリストに明示的に充填を挿入すると便利なことがある．その場合はPadLeftとPadRightを使うとよい．
PadLeft[list,n]
ゼロを左側に挿入して長さ n になるように充填する
PadLeft[list,n,x]
要素 x を繰り返して充填する
PadLeft[list,n,{x1,x2,…}]
xi を循環的に繰り返して充填する
PadLeft[list,n,list]
list を循環的に繰り返して充填する
PadLeft[list,n,padding,m]
右側に m 要素のマージンを残す
PadRight[list,n]
右側にゼロを挿入して充填する
リストの充填
リストの長さが6になるように充填する：
Wolfram Language code: PadLeft[{a, b, c}, 6]
{x,y}を循環的に挿入して充填する：
Wolfram Language code: PadLeft[{a, b, c}, 6, {x, y}]
これは右側にも3のマージンを残す：
Wolfram Language code: PadLeft[{a, b, c}, 10, {x, y}, 3]
PadLeft，PadRight，Partitionはネストしたリストに使うことができる．
これで3×3の配列を作る：
Wolfram Language code: PadLeft[{{a, b}, {e}, {f}}, {3, 3}, x]
この配列をオフセット1で2×2のブロックに分割する：
Wolfram Language code: Partition[%, {2, 2}, {1, 1}]
充填指定にネストしたリストを使うと，各レベルでリストの要素が循環的に使われる．
こうすると充填リストのコピーが循環的に使われる：
Wolfram Language code: PadLeft[{{a, b}, {e}, {f}}, {4, 4}, {{x, y}, {z, w}}]
これは充填のみからなるリストである：
Wolfram Language code: PadLeft[{{}}, {4, 4}, {{x, y}, {z, w}}]
疎な（スパース）配列：リストの操作
通常Wolfram言語ではリストは要素の明示的なリストを与えて指定する．しかし，大きな配列を扱っているような場合には，特定の位置における要素の値が何かだけを指定し，その他の要素はすべてデフォルト値（通常ゼロ）にすることができると便利なことがある．WolframシステムではSparseArrayオブジェクトを使ってこうすることができる．
{e1,e2,…}
,
{{e11,e12,…},…}
,
…
通常のリスト
SparseArray[{pos1->val1,pos2->val2,…}]
疎な配列
通常のリストと疎な配列
疎な配列を指定する：
Wolfram Language code: SparseArray[{2 -> a, 5 -> b}]
こちらは通常のリストである：
Wolfram Language code: Normal[%]
これは二次元の疎な配列を指定する：
Wolfram Language code: SparseArray[{{1, 2} -> a, {3, 2} -> b, {3, 3} -> c}]
これは通常のリストのリストである：
Wolfram Language code: Normal[%]
SparseArray[list]
list の疎な配列版
SparseArray[{pos1->val1,pos2->val2,…}]
位置 posi で値が vali である疎な配列
SparseArray[{pos1,pos2,…}->{val1,val2,…}]
同じ疎な配列
SparseArray[Band[{i,j}]->val]
値val である帯状疎配列
SparseArray[data,{d1,d2,…}]
d1×d2×…の疎な配列
SparseArray[data,dims,val]
デフォルト値 val の疎な配列
Normal[array]
array の通常のリスト版
ArrayRules[array]
array の位置と値の規則
疎な配列の作成と変換
リストの疎な配列版を生成する：
Wolfram Language code: SparseArray[{a, b, c, d}]
通常のリストに変換し直す：
Wolfram Language code: Normal[%]
デフォルト値がxで長さが7の疎な配列を作る：
Wolfram Language code: SparseArray[{3 -> a, 5 -> b}, 7, x]
これは上記に対応する通常のリストである：
Wolfram Language code: Normal[%]
これは疎な配列で使われた規則である：
Wolfram Language code: ArrayRules[%%]
帯行列を生成する：
Wolfram Language code: SparseArray[{Band[{1, 1}] -> x, Band[{2, 1}] -> y}, {5, 5}]//MatrixForm
SparseArrayの重要な特徴は，位置の指定にパターンが使える点である．
{i_,i_}に一致するすべての位置が1である4×4の疎な配列を指定する：
Wolfram Language code: SparseArray[{i_, i_} -> 1, {4, 4}]
結果は4×4の単位行列になる：
Wolfram Language code: Normal[%]
これは余分な要素を持った単位行列である：
Wolfram Language code: Normal[SparseArray[{{1, 3} -> a, {i_, i_} -> 1}, {4, 4}]]
こうすると第3列がすべてaになる：
Wolfram Language code: Normal[SparseArray[{{_, 3} -> a, {i_, i_} -> 1}, {4, 4}]]
SparseArray[rules]は可能なすべての位置指定を取り，次に rules を適用して各々の値を決定するものであると考えることができる．例によってリストの最初で与えられた規則が最初に適用される．
ランダムな対角行列を生成する：
Wolfram Language code: Normal[SparseArray[{{i_, i_} :> RandomReal[]}, {3, 3}]]
値が指標に依存する規則を使うことができる：
Wolfram Language code: Normal[SparseArray[i_ -> i ^ 2, 10]]
偶数位置にpを挿入する：
Wolfram Language code: Normal[SparseArray[{_ ? EvenQ -> p, i_ -> i ^ 2}, 10]]
代替値を含むパターンを使うことができる：
Wolfram Language code: Normal[SparseArray[{1 | 3, 2 | 4} -> a, {4, 4}]]
パターンに制約条件を付けることもできる：
Wolfram Language code: Normal[SparseArray[i_ /; 3 < i < 7 -> p, 10]]
こうすると帯対角行列ができる：
Wolfram Language code: Normal[SparseArray[{{i_, j_} /; Abs[i - j] < 2 -> i + j}, {5, 5}]]
別の例である：
Wolfram Language code: Normal[SparseArray[{Band[{1, 1}] -> {2, 4, 6, 8, 10}, Band[{1, 2}] -> {3, 5, 7, 9}, Band[{2, 1}] -> {3, 5, 7, 9}}, {5, 5}]]
いろいろな目的のために，WolframシステムはSparseArrayオブジェクトをこれに対応する他の通常のリストと同じように扱う．このため，例えば疎な配列オブジェクトの部分を問うと，Wolframシステムは対応する通常のリストにおける部分について問われたかの如き処理をする．
これは疎な配列オブジェクトを生成する：
Wolfram Language code: s = SparseArray[{2 -> a, 4 -> b, 5 -> c}, 10]
これは上記に対応する通常のオブジェクトである：
Wolfram Language code: Normal[s]
疎な配列の部分はこれに対応する通常の部分と同じである：
Wolfram Language code: s[[2]]
この部分はデフォルト値0である：
Wolfram Language code: s[[3]]
多くの操作でSparseArrayオブジェクトは通常のリストと同じように扱われる．可能な場合は結果として疎な配列が返される．
これは疎な配列を与える：
Wolfram Language code: 3 s + x
これは対応する通常のリストである：
Wolfram Language code: Normal[%]
Dotは疎な配列オブジェクトに直接働く：
Wolfram Language code: s.s
疎な配列と通常のリストを混ぜることもできる：
Wolfram Language code: s.Range[10]
Wolframシステムは疎な配列をSparseArrayという頭部を持つ式として表す．疎な配列は評価されると常にSparseArray[Automatic,dims,val,…]という構造を持つ最適化された標準形に変換される．
しかしこの構造がはっきりすることはあまりない．Lengthのような操作でさえも結果は対応する通常のリストで与え，生のSparseArray式構造では与えないようになっているからである．
これは疎な配列を生成する：
Wolfram Language code: t = SparseArray[{1 -> a, 5 -> b}, 10]
これが根底にある最適化された式構造である：
Wolfram Language code: InputForm[%]
Lengthは対応する通常のリストの長さを与える：
Wolfram Language code: Length[t]
Mapもまた個々の値に働く：
Wolfram Language code: Normal[Map[f, t]]