ニューラルネット入門

LeNetとMNISTコンテナ
層訓練
ネットエンコーダ評価
ネットデコーダ
LeNetとMNIST
このチュートリアルでは，1桁の手書き数字の画像を入力として取り，その数字を予測するネットを訓練する方法を示すことによって，Wolfram言語のニューラルネットフレームワークの概要を紹介する．訓練に使うデータ集合はMNISTデータ集合であり，Wolfram Neural Net Repositoryで利用可能な 最初のたたみ込みネットの一つであるLeNetの変形を訓練する．
6万の訓練画像と1万の検証画像を含む，MNISTデータ集合を取得する：
訓練集合からランダムな例をいくつか表示する：
Wolfram Neural Net Repositoryから事前に訓練されたLeNetを得る：
事前に訓練されたネットを使って，画像のリストを分類する：
LeNetのようなネットワークを一から訓練することは非常に簡単である．NetTrainを使うことで，適切な損失関数を選んだり，エンコーダやデコーダを加えたり，バッチサイズを選んだりすることが自動的に処理される．これを次で見てみる．
LeNetを一から訓練する：
しかし，これでこのチュートリアルが終る訳ではない．
Wolfram言語におけるディープラーニングの基本を提示するために，コンポーネント層からLeNetを構築し，損失関数を選び，訓練ネットワークを定義し，エンコーダとデコーダを加え，最後にネットワークを訓練して評価する，という「難しい方法」を行ってみる．この特定のタスクの裏側にある一般原則を理解することで，Wolfram言語を使って簡単に，しかも効率的に高度な学習タスクに取り組むことができるようになる．
層
ニューラルネットワークの最も基本的な構成要素は「層」である．層は，数の配列を変換する単純な関数と捉えることができる．
事前に訓練されたLeNetモデルをもう一度見てみよう（構成層を表示するために表示フォームのボタンをクリックしたものである）．
ネットはConvolutionLayer，PoolingLayer等のさまざまな層からなっている．これらの層のそれぞれが異なるタスクを遂行している（この場合はコンピュータビジョンに関するタスク）．
ネットの最後の層を見てみる．
NetExtractを使って，ネットの最後の層を抽出する：
この層についての多くの情報が見えるようになった．例えばこれは入力として長さ10のベクトルを想定しており，同じ長さのものを返す．
他の層と同様に，この層を入力に適用して出力を得ることができる:
層はNumericArray入力を取ることもできる．この場合はNumericArrayを出力する：
SoftmaxLayerは総和が1となる確率を出力するためのものである．
上の出力を足す：
新しい層を構築する．
入力として長さ2のベクトルを取り，出力として長さ3のベクトルを生成するLinearLayerを作成する：
上の要約ボックスでは，「uninitialized」というキャプションが表示されている．これは，まだ提供されていない学習可能なパラメータがネットに含まれていることを意味する．
初期化されていない層を入力ベクトルに適用すると次のようになる：
ConvolutionLayerやLinearLayer等，一部の層だけが学習可能なパラメータを持つ．そのような層は常に表示フォームに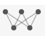アイコンを含んでいる．これに対して，アイコン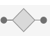を持つ層は学習可能なパラメータを含んでいない．
NetInitializeを使うと，学習可能なパラメータにランダムな値を与えることができる．
層を初期化する：
初期化された層を入力ベクトルに適用する：
初期化された層から重みとバイアスを取得する：
層の重みとバイアスのパラメータはNumericArrayに詰められる．これらはNormalを使ってリストに変換することができる：
ここまでは1つの入力だけを取る層を見てきた．層の中には2つ以上の入力を取るものもある．例えば，MeanSquaredLossLayerは「入力」と「ターゲット」という2つの配列を比較し，Mean[(input-target)^2]を表す1つの数を出力する．
MeanSquaredLossLayerを作成する：
層の入力は名前が付いているので，ネットが適用されるときは連想で与えられなければならない．
層を2つの入力に適用する：
層にはニューラルネットフレームワークに特有の機能を導入するものもあれば，既存のWolfram言語のシンボルの機能に酷似したものもある．例えば，FlattenLayerはFlattenに，DotLayerはDotによく似ている．
利用可能な層の完全リストは以下の通りである．

層のその他の特性（高度なトピック）

このセクションでは，Wolfram言語におけるニューラルネットの層の主な特性をいくつかまとめる．
ネットエンコーダ
ニューラルネットの層は基本的に「微分可能」でなければならないので，配列に作用する．しかし，画像，音声，テキスト等別のデータでネットを訓練し使用したい場合もある．この場合，NetEncoderを使うとこのデータを値の配列に変換することができる．
MNISTデータ集合の数字の画像を変換するために，"Image"エンコーダを使う．実際どのように使われるかを示す簡単な例を見てみよう．
1×12×12配列を出力する画像NetEncoderを生成する：
画像NetEncoderを画像に適用する：
画像エンコーダは，画像を配列に変換する前に，画像が指定された色空間，次元等を持つようにする．
画像NetEncoderを大きいカラー画像に適用する：
上で行ったように，エンコーダはネットとは独立で使用することができるが，層に加えて使う方が一般的である．これは，層を作成するときにでも後ででも行うことができる．次はエンコーダを付けた層を作成する例である．
"Input"オプションを使って画像NetEncoderをPoolingLayerに加える：
PoolingLayerを直接画像に適用する．ここで画像NetEncoderを使って，PoolingLayerが適用できるように画像を配列に変換する．
出力を画像に戻す：
MNISTの実際の画像は，サイズ28×28のグレースケール画像である．ここで最終的な画像エンコーダを作成しよう．後でLeNetを最初から構築するときにこのNetEncoderを加える．
MNISTの"Image"エンコーダを作成する：
このエンコーダの次元は，MNISTデータ集合の画像の次元に一致する：
ネットデコーダ
ニューラルネットの出力は予測であることが多い．回帰問題では，この予測は通常推定値，つまりネットがタスクに対して最もあり得ると推定する値を表す1つの数値である．このような出力は通常復号化される必要はない．
しかし，分類問題の場合，ネットの出力は通常，要素が各クラスの確率を表すベクトルである．例えば，食べ物の画像を「ホットドッグ」，「ピザ」，「サラダ」と分類するネットは，この3つのクラスの確率を表す和が1となる，3つの成分を持つベクトルを出力する．
このような確率ベクトルの出力では，通常生の確率ではなく「最もあり得る」クラスに関心がある．これを決めるためには，クラスが特定のベクトル成分とどのように関連付けられているかを知る必要がある．
上位 n 個の確率（多数のクラスがある場合），指定したクラスの確率，予測の不確実性の測定等，確率ベクトルから計算できる特性は他にもある．
このようなクエリをもっと簡単にするために，"Class" NetDecoderを使ってベクトル成分とクラスの間のマッピングを保存し，ネットの出力を自動的に解釈するすることができる．出力をImage，ブール値等に変換するための他の種類のNetDecoderも可能であるが，このチュートリアルではそこまでの詳細には言及しない．
MNISTのタスクでは，使用する10個のクラスは数字の0から9である．適切なデコーダを作成しよう．
"Class" NetDecoderを作成して，確率ベクトルを解釈する：
デフォルトでは，デコーダは確率ベクトルを最もあり得るクラスとして復号化する（これが難しく思えたら，最初のクラスが0ということを思い出すとよい）．
デコーダを確率ベクトルに適用する：
ネットを適用するときに，第2引数として名前付きの特性を与えると，別の特性を計算することができる．
最も可能性の高いクラスとその確率のリストを得る：
指定したクラスの確率を求める：
確率の完全なリストを連想として取得する：
予測の不確実性の測定値を得る：
NetEncoderの場合と同様に，層の出力にNetDecoderを加えることができる．以下は先に提示したPoolingLayerのより合理化された例である．ここでは"Image" NetEncoderを使って層への入力を解釈し，"Image" NetDecoderを使って層の最終的な出力を画像に戻す．
NetEncoderとNetDecoderの両方を層に加える：
層を画像に適用すると，画像が生成される：
コンテナ
1層のニューラルネットは，それ自体では通常あまり役に立たない．何かを達成するためには，複数の層をまとめることが必要になる．
最も簡単に層をまとめる方法は，次々と繋いでいくことである．これでは，最初の層の出力が次の層の入力として使われる．このように層を繋ぐにはNetChainコンテナを使うとよいが，もっと複雑な接続方法が必要な場合はNetGraphを使う．
ここでは単純にチェーンで繋いでみる．
Cos[Sin[x]]を計算する簡単なNetChainを作成する：
このNetChainを入力に適用し，その結果と，同じ入力にSin，Cosを順に適用した結果を比較する：
Ramp関数の後にSoftmaxLayerを適用するElementwiseLayerからなる簡単なNetChainを作成する：
NetChainを入力に適用する：
その結果は，ここの層を順に適用していったものと同じである：
コンテナの重要な特性は，層として動作することであり，他のコンテナの中でも層として使えるということである．この例を見てみよう．
先のNetChainを別のNetChainの中にネストする：
チェーンを入力に適用する：
ネストされたチェーンを平滑化する：
先にLeNetモデルを見たが，これはより複雑なチェーンである．ついは初期化されていないLeNetを構築するコードである．
最初からLeNetを構築し，先ほど構築したNetEncoderとNetDecoderを与える：
学習可能なパラメータを含む総は赤で表示されており，ネットが入力に適用されるまでに初期値が必要であることを示している．
練習として，LeNetをランダムに初期化し，それをMNISTのサンプル入力に適用する．得られる出力も乱数であるが，適切に動作していることは分かる．
LeNetの学習可能パラメータをランダムに初期化する：
初期化されたLeNetを入力画像に適用して，ランダムに分類する：
高い可能性を持つもののソートされたリストを取得する：
もちろん最終的な目標は，このランダムに初期化されたネットワークが手書き数字を正しく分類するよう訓練することである．

グラフ

LeNetを訓練するためには，個々の訓練の例をLeNetに与える「訓練ネットワーク」を構築する必要がある．MNISTデータ集合の訓練の例はどれも，入力画像とそれに対応するターゲットラベルの組み合わせからなる．
MNISTの例の集合を表示する：
NetChainではネットは2つ以上の入力を取ることができないため，訓練ネットワークを構築するためにはNetGraphを使う必要がある．訓練ネットワークのタスクは，LeNetによって生成された予測を評価することであり，予測が正しい場合は小さい数字を生成し，正しくない場合は大きい数字を生成する．これは「損失」と呼ばれる．これは予測誤差のある種の代用物と見ることができる．
この訓練ネットワークが準備できたら，NetTrain関数を使って，時間の経過とともに損失が減少するように，ネットの学習可能パラメータを徐々に変更することができる．
異なる学習タスクでは，損失を計算するのに異なる方法が使われなければならない．MNISTの数字の分類等の分類タスクでは，よくある損失は「交差エントロピー」である．層CrossEntropyLossLayerは，予測と真のラベル（またはターゲット）が与えられると，この損失を計算することができる．
使用する予測は確率ベクトルの形式である．ここで，ベクトルの各要素は，対応する数字0，1，2等を表す．ターゲットラベルは正しいクラス（数字0には1，数字1には2等）の指標である．
次は，予測を採点するのに使われるCrossEntropyLossLayerの簡単な例である．
ターゲットラベルを持つ長さ5の入力の予測ベクトルを計算するCrossEntropyLossLayerを作成する：
損失層を，最初の成分が大きい確率を持つ予測ベクトルに適用する：
予測は高い確率をクラス1に関連付けているので，ターゲットが1の場合，損失は低い：
予測は低い確率をクラス5に関連付けているので，ターゲットが5の場合，損失は高い：
構築する訓練ネットは単純である．これはLeNetを数字の画像に適用し，予測を出力し，その予測とターゲットクラスを比較するというものである．
層と接続のリストを与えることによってNetGraphを構築する．グラフへの入力はNetPort["input"]destination を使って層と接続され，損失層への入力はsource->NetPort["loss","input"]で接続される：
検証するために，入力の集合とそれに対応するターゲットについて，ランダムに初期化された予測LeNetを含む訓練ネットを使ってみよう．
"Input"ポートに画像のリストを，"Target"ポートに指標のリストを与える：
これらの損失は，LeNetが，与えられた画像についてうまくターゲットを予測していることを示している．LeNetはランダムに初期化されたため，平均して偶然にすぎないと予測する．訓練中，LeNetの学習可能パラメータは徐々に平均損失を引き下げるよう調整されている．
どれはどのようにして可能になったのだろうか．ここで重要なのが「勾配」である．勾配は，誤差逆伝播法と呼ばれる処理を介して計算できる，学習可能なパラメータの調整である．この調整は，指定された一団の例での訓練ネットの平均損失をわずかに減少させるために導かれる．
一団の例をランダムに繰返し選び，調整を計算し，それを学習可能なパラメータに適用することによって，ネットは所望されたタスクで徐々に向上を見せる．
この過程は，訓練課程を調整あるいは微調整する方法を多数提供するNetTrainによって処理される．しかし，NetPortGradientを使って，これらの勾配の一つを直接計算することによって，関連するメカニズムの本質を垣間見ることができる．
LeNetの最初のたたみ込み層のバイアスにおける特定の入力によって生成された勾配を要求する：
これで勾配が得られたので，この例の損失を減少させるこの勾配を使って，対応する学習可能なパラメータを実際に修正することができる．
バイアス値を得ることによって，訓練ネットの値を修正し，その勾配を使って値を調整し，それをもとのネットで置き換える：
修正されたネット上の損失と下のネットを比較する．損失は減少している：
訓練
NetTrainを使って作成したネットワークを訓練してみる．
通常，NetTrainは訓練ネットワークを自動的に構築する．例えば，入力と出力がそれぞれ1つずつの簡単なネットワークの場合，ネットに ini を与え，適切な損失関数を使ってネットの出力を outi と比較することによって， {in->out,…}という形式の訓練データを作成する．
しかし，明示的に訓練ネットワークを構築したので，訓練データは<|"port"->list,…|>という形式で提供する必要がある．ここで訓練ネットの入力ポートに明示的にデータのリストを与える．まず in->out という規則の形式のデータを変換しなければならない．
さらに，訓練データには整数0から9のラベルが含まれ，訓練ネットの「ターゲット」入力には範囲1から10までの指標が想定されていると言う事実を説明する必要がある．"Class" NetEncoderを使ってそれらを変換する（通常NetTrainが自動的に行う）ことができるが， 1を足すだけで同じものが得られる．
KeysとValuesを使って，訓練データと検証データからそれぞれ画像とラベルを取得することによって，訓練データと検証データを連想の形式に変換する：
訓練の連想のサンプルを表示する：
ここでNetTrainを使って訓練を実行する．このネットについて以下のようなことに注意する．
LeNetを訓練する：
最後のNetTrainResultsObjectによって大量の情報が得られる．そのうちの一部は表示形式で得られるが，プログラムによってより多くの情報を取得することができる．我々のネットワークは，CPU訓練を3分行っただけで，約99.4%の正確さが達成できたことが分かる．
もう一度損失の進化を見る．
NetTrainResultsObjectから損失進化プロットを得る：
多分，最も重要なのは，最終的なネットワークが抽出できるということであろう．
NetTrainResultsObjectから訓練ネットを得て，それから予測ネットワークを抽出する：
分類ネットが訓練ネットワーク内部に埋め込まれたときに削除されたNetEncoderとNetDecoderを再度加える：
これで訓練されたネットワークが分類を実行することができるようになった．
画像を分類する：
困難な画像に対して可能性の高いものを得る：
LeNetを最初から構築し，訓練するのはこれで終了である．この過程では以下のようなトピックについて説明した．
次のセクションでは，訓練されたネットを評価する方法を説明する．
評価
ネットを訓練し終えたので，それについてもっと多くの情報を引き出すことができる．例えば，別のデータ集合についての全体的な正確さを得ることができる．また，ネットがどの程度例を誤って分類するかを要約する「混同行列」等の便利な概略を得ることもできる．深層学習を使うネットの性能を他の一般的な機械学習テクニックの性能と比較することもできる．
データ集合に対するネットの分類動作のさまざまな特性を測定するClassifierMeasurementsObjectを構築してみよう．訓練に使用しなかったデータ集合を使うことが大切なので，MNISTデータセットに同梱の検証集合を使う．
ClassifierMeasurementsを使って，検証集合に対するClassifierMeasurementsObjectを得る：
ClassifierMeasurementsObjectができたので，あらゆる種類の特性を効率的にクエリすることができる．
全体的な正確さを取得する：
損失が最も大きい例のリストを得る：
ネットのクラスに対する確信が最も低い例のリストを得る：
どのような分類の誤りが最も多いかを示すリストを取得する：
利用できる特性の完全リストを得る：
NetMeasurementsを使って，ネットのさまざまな特性を測定することもできる．NetMeasurementsとClassifierMeasurementsには，同じ特性も多数あるが，それぞれにしかないものもある．NetMeasurementsは効率的に実装されており，TargetDeviceオプションを使ってGPU上でも実行できるいう利点があるため，大規模のデータセットに非常に適している．
全体的な正確さを取得する：
混同行列を得る：
さまざまなクラスがどの程度うまく分類されているかのスコアのリストを取得する：
NetMeasurementsはニューラルネットワークについて，他の利点もある．ネットワーク内の任意の層の出力および重さを測定することができる．
訓練されたLeNetモデルの最初の層の各フィルタの平均活性率をプロットする：
さらにNetMeasurementsはキャッシュを使って，同じ特性の測定の繰返しや同様の特性の測定をスピードアップする．
カッパ係数(Cohen's Kappa)の測定時間を計る．これは上の"ConfusionMatrixPlot"の測定によりキャッシュに格納される．これはわずか一瞬で1万回測定する：
NetMeasurementsはClassifierMeasurementsよりも使える場合が多い．必要とされる損失層がないネット，NetEncoderやNetDecoderが付随しないネット，複数の出力を持つネットにも使える．
ネットと別の方法を比較する最も簡単な方法はClassifyを使うことである．これは広範に渡る一般的な方法を自動的に適用し，最適なものを選ぶ．
Classifyを使って，効率のよい機械学習モデルを自動的に選ぶ：
分類子を入力に適用する：
このニューラルネットは，検証集合に対してClassifyによって選らばれたモデルよりも性能がよい．
分類子を訓練されたネットと比較する：