Introduction to Neural Nets
This tutorial gives a brief overview of the Wolfram Language neural net framework by showing how to train a net that takes an input image of a handwritten single-digit number and then predicts the number. The dataset we are training on is the classic MNIST dataset, and we will train a variant of LeNet, one of the first convolutional nets, which is already available in the Wolfram Neural Net Repository.
It is extremely easy to train a network like LeNet from scratch. NetTrain takes care of many details of the training process automatically, such as selecting an appropriate loss function, attaching encoders and decoders and choosing a batch size. Here is what it looks like.
To give an overview of the fundamentals of deep learning in the Wolfram Language, we will now do this the hard way, by building LeNet out of its component layers, picking a loss function, defining a training network, attaching encoders and decoders, and finally training and evaluating the network. Understanding the general principles behind this particular task will put you well on the way to wielding the Wolfram Language to tackle sophisticated learning tasks easily and efficiently.
The simplest building blocks of neural nets are layers, which you can think of as simple functions that transform arrays of numbers.
Have a look at the pre-trained LeNet model again (we clicked the 
button on the display form to show the constituent layers):
button on the display form to show the constituent layers):The net is composed of a variety of layers, such as a ConvolutionLayer, PoolingLayer, etc. Each of these layers accomplishes different tasks, in this case, tasks related to computer vision.
Extract the last layer of the net using NetExtract:
We can see a lot of information about this layer. For example, it expects as input a vector of length 10 and returns the same.
The purpose of a SoftmaxLayer is to produce probabilities that sum to 1.
Create a LinearLayer that takes as input a vector of length 2 and produces as output a vector of length 3:
Notice that in the summary box above, there is an "uninitialized" caption indicating that the net contains learnable parameters that have not yet been provided.
Only certain layers, for example, ConvolutionLayer and LinearLayer, have learnable parameters. Such layers always have the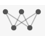 
icon in the display form. Layers with the icon 
, by contrast, do not contain any learnable parameters.
icon in the display form. Layers with the icon 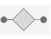, by contrast, do not contain any learnable parameters.We can supply the random values for the learnable parameters using NetInitialize.
Notice that weights and biases parameters of the layers are packed in NumericArray. They can be converted to a list using Normal:
So far, we have seen layers that have exactly one input. Some layers have more than one input. For example, MeanSquaredLossLayer compares two arrays, called the input and the target, and produces a single number that represents Mean[(input-target)^2].
Create a MeanSquaredLossLayer:
While some layers introduce functionality that is unique to the neural net framework, others mirror the functionality of existing Wolfram Language symbols. For example, FlattenLayer behaves similarly to Flatten, DotLayer behaves similarly to Dot, etc.
More Properties of Layers (Advanced)
- Layers are functions whose inputs and outputs are always arrays or scalars. In order to operate on audio, images, etc., layers must have a NetEncoder attached to the input.
- Layers perform shape inference: if the dimensions of the input are specified, then the layer can infer what the dimensions of the output will be, and vice versa.
- Layers are differentiable. Differentiability is a key property that allows for the efficient training of nets, which we will see later.
- Layers can be run using different backends (CPU, CUDA, CoreML, …) specifying the TargetDevice option.
- Layers can be trained on either a CPU or an NVIDIA GPU, by specifying the TargetDevice option.
- By default, layers evaluate using lower numerical precision (single-precision floating point) than is typical in Wolfram Language functions. The WorkingPrecision option can be used to specify different behavior.
Fundamentally, because they must be differentiable, neural net layers operate on arrays. However, we often want to train and use nets on other data, such as images, audio, text, etc. To do this, we can use a NetEncoder to translate this data to an array of values.
To translate the images of digits in the MNIST dataset, we can use an "Image" encoder. Let us first look at some simple examples of encoders in action.
Apply the image NetEncoder to an image:
The image encoder conforms the image to have the specified colorspace, dimensions, etc. before it is converted to an array.
Apply the image NetEncoder on a large color image:
While encoders can be used independently from nets, as we have done, it is more common to attach the encoder to a layer. This can be done when creating the layer or afterward. Here is an example of creating a layer with an attached encoder.
Apply the PoolingLayer directly to an image, which will use the image NetEncoder to translate the image to an array for PoolingLayer to operate on:
The actual images in MNIST are grayscale images of size 28×28. Let us create our final image encoder now. Later, we will attach this NetEncoder when we construct LeNet from scratch.
Create an "Image" encoder for MNIST:
The output of a neural net is often a prediction. For a regression problem, this prediction is typically a point estimate, which means it is a single number representing the value the net thinks is most likely for the task. Such outputs do not typically need to be decoded.
For classification problems, however, the output of the net is typically a vector whose components represent the probability of each class. For example, a net that classifies images of foods as "hot dog", "pizza", or "salad" produces a vector with three components that sum to one, representing the probabilities of those three classes.
For these kinds of probability vector outputs, we typically care about the most likely class rather than the raw probabilities. To determine this, we have to know how classes are associated with particular vector components.
There are also other properties we could also compute from a probability vector, such as the top n probabilities (if we have many classes), the probability of a specific class, or a measure of the uncertainty of the prediction.
To make these kinds of queries more convenient, a "Class" NetDecoder can be used to store the mapping between vector components and classes and thus automatically interpret the output of the net. Other types of NetDecoder are also possible, for converting the output to an Image, a Boolean value, etc., though we do not discuss them in detail in this tutorial.
For the MNIST task, the 10 classes we will use are the digits 0 through 9. Let us create an appropriate decoder.
By default, the decoder will decode a probability vector as a most likely class (if this looks confusing, recall that the first class is actually 0).
We can also compute other properties, by supplying a named property as the second argument when applying the net.
As with NetEncoder, we can attach a NetDecoder to the output of a layer. Here is a more streamlined example of the PoolingLayer we showed before, in which an "Image" NetEncoder is used to interpret the input to the layer, and an "Image" NetDecoder is used to convert the final output of the layer back to an image.
Single neural net layers are generally not useful by themselves. We usually need to combine multiple layers together to do something interesting.
The simplest way to combine layers is chain them one after another, where the output of the first layer is used as the input for the next layer, and so on. We can use the NetChain container to connect layers in this way, but when more complex forms of connectivity are required, the NetGraph container should be used instead.
Apply the NetChain to an input and compare the result to applying Sin followed by Cos to the same input:
Create a simple NetChain that consists of an ElementwiseLayer that applies the Ramp function, followed by a SoftmaxLayer:
Apply the NetChain to an input:
An important property of containers is that they act as layers and can even be used as layers within other containers. Let us see an example of that.
Previously, we saw the LeNet model, which was a more complex chain. Here is the code that constructs an uninitialized copy of LeNet.
Note that the layers containing learnable parameters appear in red, indicating that they require initial values before the net can be applied to an input.
As a quick exercise, we will now randomly initialize LeNet and apply it to a sample input from MNIST. The output we get is, of course, also random, but serves to illustrate that things are working properly.
Our ultimate goal, of course, is to teach this randomly initialized network to correctly classify handwritten digits.
Graphs
In order to train LeNet, we need to construct a training network that feeds individual training examples to LeNet. Each training example in the MNIST dataset consists of the combination of an input image and a corresponding target label.
NetChain does not allow a net to take more than one input, so we need to use NetGraph to build the training network. The task of the training network is to evaluate the prediction produced by LeNet, producing a small number if the prediction is good, and a large number if it is not. This is called a loss. It is best to think of it as a sort of proxy for prediction error.
Once we have this training network, we can use the NetTrain function to gradually modify the learnable parameters in the net so that the loss decreases over time.
For different learning tasks, different ways of computing the loss must be used. For a classification task such as classifying MNIST digits, a common choice of loss is the cross entropy loss. The layer CrossEntropyLossLayer can compute this loss when given both a prediction and a true label, or target.
The prediction we will use is in the form of a vector of probabilities, where each element of the vector represents the probability of the corresponding digit 0, 1, 2, etc. The target label is the index of the correct class (1 for digit 0, 2 for digit 1, etc.).
Here is a simple example of a CrossEntropyLossLayer being used to score a prediction.
Create a CrossEntropyLossLayer that compares an input prediction vector of length 5 with a target label:
If the target is 1, the loss will be low, as the prediction has assigned high probability to the class 1:
If the target is 5, the loss will be high, as the prediction has assigned low probability to class 5:
The training net we will construct is simple: it applies LeNet to the image of the digit to produce a prediction, and then it compares this prediction with the target class.
Construct a NetGraph by supplying a list of layers and connections. Inputs to the graph are connected to layers using the syntax NetPort["input"]destination, and the inputs to the loss layer are connected via source->NetPort["loss","input"]:
To test things out, let us use our training net, which contains a randomly initialized prediction LeNet, on a set of inputs and corresponding targets.
These losses summarize how well LeNet did at predicting the targets when given the images. Because LeNet was randomly initialized, we expect it to be no better than chance (on average). During training, the learnable parameters in LeNet are gradually adjusted to bring the average loss down.
How is this accomplished? The key idea is via gradients. These are adjustments to the learnable parameters that can be calculated through a process called backpropagation. These adjustments are derived so as to slightly reduce the average loss of the training net on a specific batch of examples.
By repeatedly selecting a batch of examples at random, calculating the adjustment, and applying it to the learnable parameters, the net gradually improves at the desired task.
This process is handled by NetTrain, which offers many ways to adjust and fine-tune the training process. But we can get some insight into the mechanism involved by calculating one of these gradients directly, using NetPortGradient.
Request the gradient produced by a specific input at the biases of the first convolution layer of LeNet:
Now that we have the gradient, we can actually modify the corresponding learnable parameter using this gradient, which reduces the loss on this example.
Modify the corresponding value of the training net by obtaining the bias value, adjusting it slightly using the gradient, and replacing it in the original net:
We are now ready to train our network with NetTrain.
Normally, NetTrain performs the construction of the training network automatically. For simple networks with one input and one output, it handles training data of the form {in->out,…} by feeding the ini to the net and then comparing the output of the net with the outi via a suitable loss function.
But because we have explicitly constructed a training network, we must provide the training data in the form <"port"->list,…>, where we explicitly feed the input ports of the training net with lists of data. So we must first convert the data we have, which is in the form of rules in->out.
As one additional complication, we must also account for the fact that the training data contains labels that are integers 0 to 9, whereas the "Target" input of our training net is expecting an index in the range 1 to 10. We could use a "Class" NetEncoder to convert them (which NetTrain would normally automate), but instead we will exploit the fact that we can just add 1 to accomplish the same thing.
Convert the training and test data into association form, using Keys and Values to obtain the images and the labels from the lists of rules in the training and test data:
Let us now perform the training using NetTrain. Notice several things about this net example:
- We have specified MaxTrainingRounds->5, which will scan the entire training set five times before finishing.
- We have given All as the third argument, to obtain a NetTrainResultsObject that summarizes various information about the training session.
- We have given a ValidationSet, which allows us to measure how well the trained classifier generalizes to new examples that it has not trained on. This helps avoid a common pitfall known as "overfitting".
- We have specified TargetDevice->"CPU" (which is already the default). If you have an NVIDIA graphics card, however, you can change this to "GPU" to achieve a big speedup in training.
The final NetTrainResultsObject gives us a wealth of information. Some of it is shown in its display form, but more information can be retrieved from it programmatically. But we can immediately see that our network was able to achieve an accuracy of about 99.4% after around 3 minutes of CPU training.
Obtain the loss evolution plot from the NetTrainResultsObject:
Obtain the trained net from the NetTrainResultsObject and from it extract the prediction network:
Reattach the NetEncoder and NetDecoder that were removed when the classification net was embedded inside the training network:
That is it! We have built and trained LeNet from scratch, and in the process covered the following topics:
- How to use NetEncoder and NetDecoder to translate between arrays and other forms of data.
- How to build a training net that computes the loss of our prediction net using CrossEntropyLossLayer.
- How to call NetTrain to train a net using training data.
Now that we have trained our net, we can derive a lot more information about it. For example, we can obtain the overall accuracy on another dataset. We can also get useful summaries like the confusion matrix, which summarizes how the net misclassifies examples. And we can compare the performance of the net, which uses deep learning, to that of other common machine learning techniques.
Let us jump in by building a ClassifierMeasurementsObject that measures various properties of the net's classification behavior on a dataset. It is important to use a dataset we did not train on, so we use the test set that comes built into the MNIST dataset.
Now that we have the ClassifierMeasurementsObject, we can query for all sorts of properties efficiently.
We can also use NetMeasurements to measure various properties of the net. NetMeasurements and ClassifierMeasurements share many of the same properties, but each have a few of their own. NetMeasurements has the advantage that it is efficiently implemented and even can be run on an NVIDIA graphics card, using the TargetDevice"GPU" option, which makes it much more applicable for large datasets.
NetMeasurements has a few other advantages for neural networks. It is possible to measure the output and weights of any layer in a network.
Additionally, NetMeasurements uses caching to speed up the repeated measurement of the same properties or even the measurement of similar properties.
Time the measurement of Cohen's Kappa, which will be cached due to measuring "ConfusionMatrixPlot" above. Note that it takes a fraction of a second to make 10000 measurements:
Finally, NetMeasurements can be used in more cases than ClassifierMeasurements: it can be used when the net has none of the required loss layers and no NetEncoder or NetDecoder attached, as well as when the net has multiple outputs.
The easiest way to compare the net to other methods is to use Classify, which automatically applies a range of common methods and chooses the best.
Use Classify to automatically pick an effective machine learning model:
The neural net outperforms the model selected by Classify on the test set.