Dendrogram
Dendrogram[{e1,e2,…}]
要素 e1, e2, …の階層的クラスタ化から系統樹を構築する.
Dendrogram[{e1v1,e2v2,…}]
構築された系統樹の viを伴う eiを表す.
Dendrogram[{e1,e2,…}{v1,v2,…}]
構築された系統樹の viを伴う eiを表す.
Dendrogram[label1e1,label2e2,…]
構築された系統樹の中でラベル labeliを使って eiを表す.
Dendrogram[data,orientation]
orientation に従って方向性のある系統樹を構築する.
Dendrogram[tree]
重み付きツリー tree に対応する系統樹を構築する.
詳細とオプション


- データ要素 eiは,数,数値リスト,数値行列,数値テンソル,ブール要素のリスト,文字列あるいは画像,地理的な位置あるいは地理実体,色およびそれらの組合せのいずれでもよい.eiがリスト,行列,あるいはテンソルのときは,それぞれが同じ次元でなければならない.
- デフォルトで,Dendrogramは上から下への方向を持つ.使用可能な方向には,Top,Left,Right,Bottomがある.
- それについてDendrogramを計算する木は頂点でしか重みを付けられない.
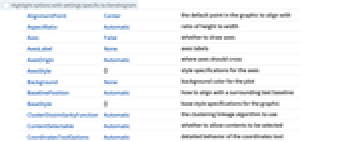
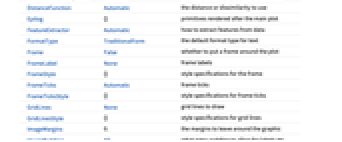
- DendrogramにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
ClusterDissimilarityFunction Automatic 使用するクラスタ化結合アルゴリズム DistanceFunction Automatic 使用する距離あるいは非類似度 FeatureExtractor Automatic どのようにしてデータから特徴を抽出するか - Dendrogramを重み付きの木に対して評価しても系統樹としてのグラフしか表示されない.最終結果が変えられるのはGraphicsのオプションだけである.
- デフォルトで,Dendrogramは,DistanceFunctionあるいはFeatureExtractorが指定されていない限り,自動的にデータを前処理する.
- ClusterDissimilarityFunctionは,メンバー要素間の非類似度が与えられた場合にクラスタ間の非類似度を定義する.
- ClusterDissimilarityFunctionの可能な設定
-
"Average" 平均クラスタ間非類似度 "Centroid" クラスタ重心からの距離 "Complete" 最大のクラスタ間非類似度 "Median" クラスタ中央値からの距離 "Single" 最小のクラスタ間非類似度 "Ward" Wardの最小分散非類似度 "WeightedAverage" 重みのついた平均クラスタ間非類似度 純関数 - 関数 f は任意の2つのクラスタからの距離を定義する.
- 関数 f はDistanceMatrixの実数値関数でなければならない.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (7)
DendrogramをClusteringTreeの結果に適用した結果と比較する:
Associationから系統樹を計算する:
これを,そのValuesの系統樹と比較する:
そのKeysの系統樹と比較する:
ベクトルをラベルに使ったArrayPlotで結果を表示する:
オプション (6)
AspectRatio (3)
ClusterDissimilarityFunction (1)
DistanceFunction (1)
自動的に選ばれたDistanceFunctionを使って系統樹を得,![]() 軸をプロットする:
軸をプロットする:
EuclideanDistanceを使って系統樹を得,![]() 軸上の値を比較する:
軸上の値を比較する:
別のDistanceFunctionを使って系統樹を得る:
FeatureExtractor (1)
アプリケーション (1)
ランダムな色のリストを生成し,y 軸上の距離を使ってその系統樹を計算する:
同じデータについて,距離が0.65未満のクラスタを統合することでClusteringTreeを計算する:
上のグラフのDendrogramを計算する:
距離の閾値が上昇するとクラスタの統合がどのようになるかを可視化するManipulateを構築する:
テキスト
Wolfram Research (2016), Dendrogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/Dendrogram.html (2017年に更新).
CMS
Wolfram Language. 2016. "Dendrogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Dendrogram.html.
APA
Wolfram Language. (2016). Dendrogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Dendrogram.html