TreePlot
✖
TreePlot
Details and Options
- TreePlot is also known as tree diagram.
- TreePlot attempts to place vertices in a tree of successive layers, or a collection of trees.
- TreePlot supports the same vertices and edges as Graph.
- If the graph g is not a tree, TreePlot lays out its vertices on the basis of a spanning tree of each connected component of the graph.
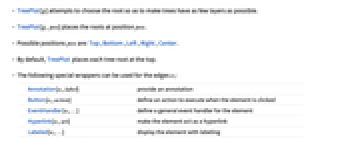
- TreePlot[g] attempts to choose the root so as to make trees have as few layers as possible.
- TreePlot[g,pos] places the roots at position pos.
- Possible positions pos are: Top, Bottom, Left, Right, Center.
- By default, TreePlot places each tree root at the top.
- The following special wrappers can be used for the edges ei:
-
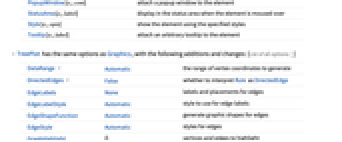
Annotation[ei,label] provide an annotation Button[ei,action] define an action to execute when the element is clicked EventHandler[ei,…] define a general event handler for the element Hyperlink[ei,uri] make the element act as a hyperlink Labeled[ei,…] display the element with labeling PopupWindow[ei,cont] attach a popup window to the element StatusArea[ei,label] display in the status area when the element is moused over Style[ei,opts] show the element using the specified styles Tooltip[ei,label] attach an arbitrary tooltip to the element - TreePlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
DataRange Automatic the range of vertex coordinates to generate DirectedEdges False whether to interpret Rule as DirectedEdge EdgeLabels None labels and placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic styles for edges GraphHighlight {} vertices and edges to highlight GraphHighlightStyle Automatic style for highlight LayerSizeFunction (1) the height to allow for each layer PerformanceGoal Automatic aspects of performance to try to optimize PlotStyle Automatic graphics directives to determine styles PlotTheme Automatic overall theme for the graph VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Automatic size of vertices VertexStyle Automatic styles for vertices - Possible settings for PlotTheme include common base themes:
-
"Business" a bright, modern look appropriate for business presentations or infographics 
"Detailed" identify data by employing labels and tooltips 
"Marketing" elegant, eye-catching design suitable for marketing needs 
"Minimal" simple graph 
"Monochrome" single-color design 
"Scientific" candid design useful for analyzing detailed data with labels and tooltips 
"Web" clean, bold design suitable for a consumer website or blog 
"Classic" historical design of graph to remain compatible with existing uses - Graph feature themes affect the plots of vertices and edges. Feature themes include:
-
"LargeGraph" large graph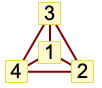 
"ClassicLabeled" classic graph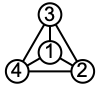 
"IndexLabeled" index-labeled graph -
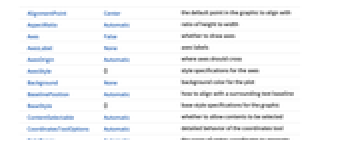
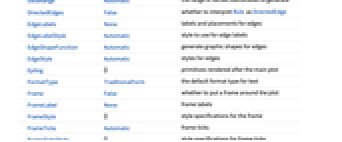
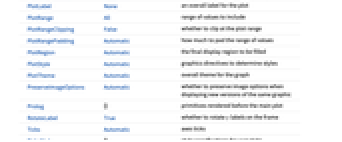
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DataRange Automatic the range of vertex coordinates to generate DirectedEdges False whether to interpret Rule as DirectedEdge EdgeLabels None labels and placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic styles for edges Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GraphHighlight {} vertices and edges to highlight GraphHighlightStyle Automatic style for highlight GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels LayerSizeFunction (1) the height to allow for each layer Method Automatic details of graphics methods to use PerformanceGoal Automatic aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to determine styles PlotTheme Automatic overall theme for the graph PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Automatic size of vertices VertexStyle Automatic styles for vertices
List of all options
Examples
open allclose allBasic Examples (5)Summary of the most common use cases
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-c2e6nq
Out[1]=1
Plot a graph specified by edge rules:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-mvn7sa
Out[1]=1
Plot a graph specified by its adjacency matrix:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-5e35s0
Out[1]=1
Drawing a tree with different orientation from the default:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-gy4ael
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-nmvutn
Out[1]=1
Scope (10)Survey of the scope of standard use cases
Graph Specification (4)
Specify a graph using a graph:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-8hiwwx
Out[1]=1
Specify a graph using a rule list:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-jiad
Out[1]=1
Specify a graph using a dense adjacency matrix:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-es74ar
Out[1]=1
Specify a graph using a sparse adjacency matrix:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-xxsr21
Out[1]=1
Graph Styling (6)
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-zhs97y
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-5uamzl
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-rnd2yf
Out[1]=1
Plot a disconnected graph using different packing methods:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-t9579j
Out[1]=1
For large graphs, it is sometimes better not to draw vertices at all:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-lq7nc5
Out[1]=1
Drawing a tree with different orientations:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-td3ovg
Out[1]=1
Options (7)Common values & functionality for each option
DataRange (1)
LayerSizeFunction (2)
PlotStyle (3)
Specify an overall style for the graph:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-76lbrw
Out[1]=1
PlotStyle can be combined with VertexShapeFunction, which has higher priority:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-fi00m0
Out[1]=1
PlotStyle can be combined with EdgeShapeFunction, which has higher priority:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-6taktx
Out[1]=1
Applications (8)Sample problems that can be solved with this function
Define a complete binary tree of depth 3:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-btazkc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tzs3626-lljiqm
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-c9gd
Out[1]=1
Generate and plot a random tree:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-y8gi9
Out[1]=1
Delete random connections in a binary tree:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-e8xmz6
Out[1]=1
Link a number with one that is rotated one bit right:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-mujdbz
Out[1]=1
Link a number with one that is rotated one bit left:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-of5pzk
Out[1]=1
Link a number with itself but with the last bit dropped:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-766ee4
Out[1]=1
Link a number with itself but with the first bit dropped:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-x8r192
Out[1]=1
Properties & Relations (4)Properties of the function, and connections to other functions
If the graph is not a tree, it is laid out based on a spanning tree of this graph:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-grz43j
Out[1]=1
Use LayeredGraphPlot for hierarchical-style drawing of a directed graph:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-rlz43l
Out[1]=1
Use GraphPlot or GraphPlot3D for general undirected graph drawing:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-dwuvuw
In[2]:=2
✖
https://wolfram.com/xid/0tzs3626-6acnjl
Out[2]=2
Use ArrayPlot or MatrixPlot to display sparse matrices:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-u08exi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tzs3626-s0w9v2
Out[2]=2
Possible Issues (2)Common pitfalls and unexpected behavior
For nontree graphs, edges may overlap:
In[2]:=2
✖
https://wolfram.com/xid/0tzs3626-ikb9pp
Out[2]=2
Use LayeredGraphPlot or GraphPlot to avoid overlapping edges:
In[4]:=4
✖
https://wolfram.com/xid/0tzs3626-c6hbdm
Out[4]=4
In[8]:=8
✖
https://wolfram.com/xid/0tzs3626-d1p4ut
Out[8]=8
TreePlot automatically chooses the base node to minimize tree height:
In[1]:=1
✖
https://wolfram.com/xid/0tzs3626-wm5sau
Out[1]=1
Explicitly specify a top node, which in this case is also the root node:
In[2]:=2
✖
https://wolfram.com/xid/0tzs3626-0mkd2
Out[2]=2
Wolfram Research (2007), TreePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/TreePlot.html (updated 2020).
✖
Wolfram Research (2007), TreePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/TreePlot.html (updated 2020).Text
Wolfram Research (2007), TreePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/TreePlot.html (updated 2020).
✖
Wolfram Research (2007), TreePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/TreePlot.html (updated 2020).CMS
Wolfram Language. 2007. "TreePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/TreePlot.html.
✖
Wolfram Language. 2007. "TreePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/TreePlot.html.APA
Wolfram Language. (2007). TreePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreePlot.html
✖
Wolfram Language. (2007). TreePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreePlot.htmlBibTeX
✖
@misc{reference.wolfram_2025_treeplot, author="Wolfram Research", title="{TreePlot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/TreePlot.html}", note=[Accessed: 25-March-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_treeplot, organization={Wolfram Research}, title={TreePlot}, year={2020}, url={https://reference.wolfram.com/language/ref/TreePlot.html}, note=[Accessed: 25-March-2025
]}