DiscreteLimit

DiscreteLimit[f,k∞]     k が整数上で無限大に近付くときの数列 f の極限k∞f(k)を与える．

DiscreteLimit[f,{k1,…,kn}]

整数上のネストした極限⋯ f(k1,…,kn)を与える．

DiscreteLimit[f,{k1,…,kn}{,…,}]

整数上の多変量極限f(k1,…,kn)を与える．

詳細とオプション

  • DiscreteLimitは，整数上の離散極限あるいは極限としても知られている．
  • DiscreteLimitは数列 f の変数 k あるいは kiが任意に大きくなるときの極限値を計算する．
  • DiscreteLimit[f,k∞]は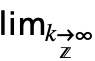fで入力できる．テンプレート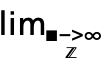はdlimで入力し，を使って真下付き文字から本体にカーソルを移動する．
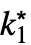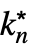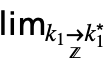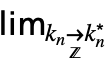  • DiscreteLimit[f,{k1,…,kn}{,…,}]は…f で入力できる．
  • 可能な極限点 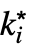は±∞である．
  • 有限極限値 f*について
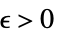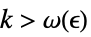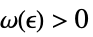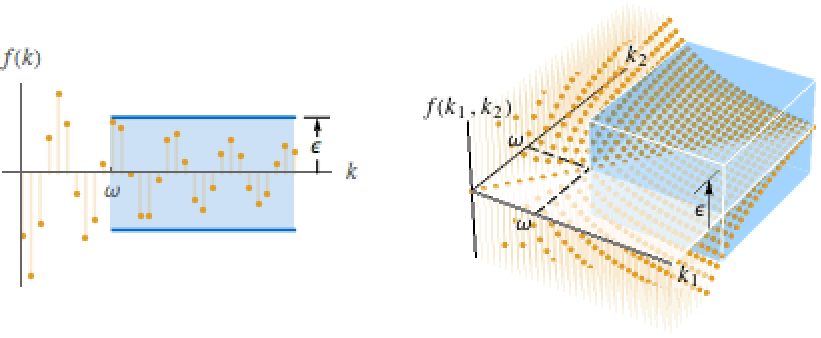
  • DiscreteLimit[f,k∞]f*すべての について， がTemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
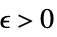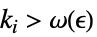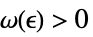    DiscreteLimit[f,{k1,…,kn}{∞,…,∞}]f*すべての について，がTemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
  • DiscreteLimit[f[k],k-∞]はDiscreteLimit[f[-l],l∞]等に等しい．
  • DiscreteLimitは，極限が存在しないと証明できる場合はIndeterminateを返し，極限が求まらないときは未評価で返される．
  • 使用可能なオプション
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Automaticパラメータについての条件を生成するかどうか
    Method Automatic使用するメソッド
    PerformanceGoal "Quality"パフォーマンスのどの面について最適化するか
  • GenerateConditionsの可能な設定
  • Automatic一般的ではない条件のみ
    Trueすべての条件
    False条件なし
    None条件が必要なときは未評価で返す
  • PerformanceGoalの可能な設定には，$PerformanceGoal，"Quality"，"Speed"がある．"Quality"と設定すると，DiscreteLimitでより多くの問題が解かれたり単純な結果が与えられたりするが，時間とメモリ消費は大きくなる可能性がある．

例題

すべて開くすべて閉じる

例  (4)

数列の極限：

数列とその極限をプロットする：

多変量数列の極限：

数列とその極限をプロットする：

dlim を使ってテンプレートを入力し，を使って真下付き文字から本体に移動する：

TraditionalFormによる表現：

スコープ  (37)

基本的な用法  (4)

n がInfinityに近付く際の数列の極限を計算する：

n が-Infinityに近付く際の数列の極限を計算する：

多変量数列についてのネストした極限を計算する：

数列のリストの極限を計算する：

初等関数数列  (7)

有理数列の極限を求める：

等比数列：

指数数列：

三角数列：

逆三角数列：

対数数列：

ArcTan[Log[n]]の極限を求める：

整数関数数列  (5)

二項数列の極限を計算する：

FactorialPowerを含む数列の極限：

Factorialを含む数列の極限：

FibonacciとLucasLを含む極限を計算する：

Pochhammerを含む極限：

交代数列  (3)

収束交代数列：

発散交代数列：

振動交代数列：

周期数列  (3)

周期数列を含む極限：

最終的に周期的になる数列：

密に非周期的な数列：

区分関数数列  (3)

収束区分数列：

発散区分数列：

周期条件がある区分数列：

Floorを含む極限：

整数論関数数列  (4)

Primeを含む極限を計算する：

Primeの位数は である：

PrimePiを含む極限：

PrimePiの位数は である：

PartitionsPとPartitionsQを含む極限：

他の整数論的数列を含む極限：

ネストした数列と多変量数列  (2)

ネストした数列の極限を計算する：

数列とその極限をプロットする：

多変量数列の極限：

形式数列  (6)

Inactiveな和を含む数列の極限を計算する：

Inactiveな和のネストした極限：

DiscreteLimitとSumを交互に使って2ステップで同じ結果を得る：

Inactiveな積を含む数列の極限：

Inactiveな積のネストした極限：

DiscreteLimitとProductを交互に使って2ステップで同じ結果を得る：

Inactiveな連分数を含む数列の極限：

Inactiveな連分数を含むネストした極限：

DiscreteLimitとContinuedFractionKを使って2ステップで同じ結果を得る：

オプション  (6)

Assumptions  (1)

パラメータについての仮定を指定する：

仮定が変わると結果が変わることがある：

GenerateConditions  (3)

条件を述べずに結果を返す：

この結果は y>1のときにのみ有効である：

結果がパラメータの値に依存する場合は未評価で返す：

デフォルトで，一意的な結果を返す条件が生成される：

デフォルトで，特殊な値が結果を無効にするときにのみ条件が生成されなくなる：

GenerateConditions->Trueとすると，このように一般的ではない条件もレポートされる：

Method  (1)

デフォルトメソッドを使って数列の極限を計算する：

Limitへの呼出しを使って同じ答を得る：

与えられた数列は周期的ではないので，周期数列用のメソッドはうまくいかない：

PerformanceGoal  (1)

DiscreteLimitは，任意の大周期の数列を含む極限を計算する：

そのような場合にコストが高くなりそうな計算をPerformanceGoalを使って回避する：

MethodオプションはPerformanceGoalをオーバーライドする：

アプリケーション  (35)

幾何極限  (3)

半径 r で辺の数が n の正多角形の外周：

n->∞のとき，外周は半径 r の円の円周に近付く：

半径 r で辺の数が n の正多角形の面積：

n->∞のとき，これは半径 r の円の面積に近付く：

n が大きくなるにつれて，内接多角形，外周と面積の近似値が変化する様子を可視化する：

図示したように，半径 r の球を 2n 個の円柱で被覆することを考える：

円柱の体積：

DiscreteLimitを n->Infinityで使うと球の体積が返される：

直接計算した場合と比較する：

以下の関数とそのプロットで定義された矩形の集合について考える：

区間[0,2]で n5のときの矩形：

これらの矩形の面積は，曲線下の面積を近似するリーマン(Riemann)和を定義する：

DiscreteLimitを使って厳密な答を得る：

Integrateを使って同じ面積を直接得る：

この関数および他の3つの関数の過程を可視化する：

和と積  (6)

無限和を有限和の極限として計算する：

Sumを使って同じ答を得る：

次の数列は収束級数を定義する：

この級数の値を求める：

Sumを使って結果を直接計算する：

有限個の項の和から始めて，無限級数が発散することを証明する：

有限和の極限は存在しないので，この級数は発散する：

SumConvergenceとSumを使って発散を確認する：

Regularizationを使って，この級数のアーベル(Abel)和を求める：

有限和のネストした極限として二重無限和を計算する：

Sumを直接使って同じ答を得る：

有限積の極限として無限積を計算する：

Productを使って同じ答を得る：

反復無限小変換の極限として回転行列を構築する：

方向構築と比較する：

級数収束  (4)

一般項が以下で与えられる級数の収束を，比判定法を使って検証する：

この級数のDiscreteRatioを計算する：

比の極限が1より小さいので，この級数は収束する：

SumConvergenceを使って結果を検証する：

一般項が以下で与えられた級数の収束を，ベキ根判定法を使って検証する：

n 乗根が1より小さいので，この級数は収束する：

SumConvergenceを使って結果を検証する：

一般項が以下で与えられる級数の収束を，ラーベ(Raabe)判定法を使って検証する：

比判定法では結論が出ないので，ラーベ判定法を適用する：

次の極限が1より大きいので，この級数は収束する：

SumConvergenceを使って結果を検証する：

一般項が以下で与えられる級数の発散を，発散判定法を使って検証する：

一般項の極限が0ではないので，この級数は発散する：

SumConvergenceを使って結果を検証する：

従来の定義  (3)

次の数列が0に収束することを示し，ϵ=1/7で従来の定義を検証する：

極限を計算する：

の値を設定する：

この定義がすべての n>=12を満足することをReduceを使って示す：

DiscretePlotを使って結果を検証する：

次の数列がInfinityに発散することを示し，M=35で従来の定義を検証する：

極限を計算する：

Mの値を設定する：

この定義がすべての n >= 10を満足することをReduceを使って示す：

DiscretePlotを使って結果を検証する：

項が以下で与えられる調和級数 が収束するかどうかを見る：

比判定法のような一般的な判定法では結論が出ない：

補級数 を次のように定義する：

の項はの長さの連からなる：

であることに注意のこと：

また，各連の和はなので，最初の項の和はである：

の部分和は調和数 TemplateBox[{n}, HarmonicNumber]と呼ばれる：

任意の正の整数 について TemplateBox[{{2, ^, {(, {{2, , M}, -, 2}, )}}}, HarmonicNumber]>=sum_(n=1)^(2^(2 M-2))a(n)=M であるので，TemplateBox[{n}, HarmonicNumber]はいずれ を超え，に発散する：

このことは，の和が収束しないことを意味する：

しかし，発散はゆっくりで，を超えるまでにを超える項数が必要である：

回帰数列  (3)

RSolveValueを使って指定された非線形回帰数列の極限を計算する：

RSolveValueを使って指定された三角回帰数列の極限を計算する：

の値を計算する：

数学定数  (5)

数列の極限として を計算する：

Sumの極限として を計算する：

数列の極限として を計算する：

数列の極限を使ってEulerGammaを計算する：

Fibonacciを含む数列を使って黄金比を計算する：

数学関数  (2)

を記号項を含む数列の極限として表す：

Log[x]を数列の極限として表す：

シュトルツ・チェザロの定理  (2)

シュトルツ・チェザロ(Stolz–Cesàro)の定理は，ロピタルの定理の離散版で，適切な条件のもとで数列の比の極限の計算に使うことができる．以下がその定理である：

以下で定義される数列についてのシュトルツ・チェザロの定理を検証する：

差の比について極限を計算する：

DiscreteLimitを直接使って同じ結果を得る：

数列と極限をプロットする：

以下で定義される数列についてのシュトルツ・チェザロの定理を検証する：

差の比の極限を計算する：

DiscreteLimitを直接使って同じ結果を得る：

数列とその極限をプロットする：

計算の複雑性  (3)

のとき，アルゴリズムのランタイム関数 は「little-o of 」（）であると言われる：

同様に，のとき， は「little-omega of 」（）であると言われる：

であれば ：

2つの関数がどちらの関係も共有しないこともある：

さらに，どちらの関係も関数とそれ自身との間で成り立たないこともある：

したがって， と はアルゴリズムのランタイムの空間上で半順序を定義する：

大きい入力に対して と関連付けられたアルゴリズムが と関連付けられたアルゴリズムよりもはるかに速いときは，：

は逆の関係を表す：

とは比較できないので，2つのリストは厳密に逆の関係ではない点に注意のこと：

以下が成立するなら，アルゴリズムランタイム関数 は「big-theta of 」（）であると言われる：

実行に時間 がかかるアルゴリズム（次数 の多項式）について考える：

この関数の単項式 との比は，無限大における首位係数 に達する：

この数列には極限があるので，最大極値と最小極値はどちらもこの値と一致しなければならない：

アルゴリズムランタイムについて，すべての多項式アルゴリズムが となるためには，は正の有限数でなければならない：

したがって，大きい入力のランタイムの決定には，多項式の首位項のみが重要である：

高速フーリエ変換の漸近的複雑性をチェックする：

漸近的複雑性を計算する：

一様収束  (2)

関数 の次の数列は，すべての点 で0に収束する：

各 は で大きさが最大になる：

したがって，任意の について，はすべての でTemplateBox[{{{f, _, n}, (, x, )}}, RealAbs]<epsilon となり収束が一様であることを暗示する：

結果として，積分の極限は極限の積分に等しい：

すべての点 について，関数 の次の数列は0に収束する：

しかし，点 に の最大値は で発散する：

このことは，関数の数列の収束が一様ではないことを示している：

結果として，積分の極限は極限の積分とは一致しない：

さまざまな応用  (2)

ポスト(Post)の反転公式を使って の逆ラプラス変換を計算する：

この関数の逆ラプラス変換は1である：

InverseLaplaceTransformを使って同じ結果を得る：

ポストの反転公式を使って基本的な逆ラプラス変換の表を作る：

確率変数の数列についての確率分布の極限は，それが存在するのなら，漸近分布と呼ばれる．確率と試行回数の積である平均値 λ が定数である二項分布の数列についての漸近分布としてのポアソン(Poisson)分布を得る：

試行回数が n->∞のときのこの数列の極限を計算する：

これがPoissonDistributionのPDFであることを検証する：

λ=8のとき n のさまざまな値についてこの分布をプロットする．すべての k>n について確率密度関数が0である点に注意のこと：

特性と関係  (15)

乗法定数は極限の外に出すことができる：

f と g が有限極限を持つとき，DiscreteLimitは和について分配的である：

f と g が有限極限を持つとき，DiscreteLimitは積について配分的である：

ベキ乗は極限の外に出すことができる：

関数構成と数列極限操作は，連続関数では入れ替えることができる：

これは，不連続関数では成り立つ必要はない：

はさみうちの定理 （またはサンドイッチ定理）：

この関数は，正の整数上の で有界である：

境界関数の極限は0である．このことはもとの極限が0であったことを証明する：

シュトルツ・チェザロの定理を使って2つの数列の比の極限を求めることができる：

極限を直接解くとタイプの不定形になる：

シュトルツ・チェザロの定理は，極限を正しく計算するために適用される：

Limitが存在するなら，DiscreteLimitも存在する．両者の値は等しい：

逆は成立しなくてもよい：

DiscreteLimitが存在するならDiscreteMaxLimitも存在する．両者の値は等しい：

DiscreteLimitが存在するならDiscreteMinLimitも存在する．両者の値は等しい：

差の極限は TemplateBox[{{{f, (, {n, +, 1}, )}, -, {f, (, n, )}}, n, infty}, DiscreteLimit]=TemplateBox[{{{(, {f, (, n, )}, )}, /, n}, n, infty}, DiscreteLimit]を満足する：

比の極限は TemplateBox[{{{(, {f, (, {n, +, 1}, )}, )}, /, {(, {f, (, n, )}, )}}, n, infty}, DiscreteLimit]=TemplateBox[{{{f, (, n, )}, ^, {(, {1, /, n}, )}}, n, infty}, DiscreteLimit]を満足する：

有限和を使って数列の極限を計算する：

有限積を使って数列の極限を計算する：

数列の極限は，最終値定理を介してそのZTransformに関連している：

最終値定理を検証する：

おもしろい例題  (1)

数列極限の集合を可視化する：

Wolfram Research (2017), DiscreteLimit, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteLimit.html.

テキスト

Wolfram Research (2017), DiscreteLimit, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteLimit.html.

CMS

Wolfram Language. 2017. "DiscreteLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteLimit.html.

APA

Wolfram Language. (2017). DiscreteLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteLimit.html

BibTeX

@misc{reference.wolfram_2024_discretelimit, author="Wolfram Research", title="{DiscreteLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLimit.html}", note=[Accessed: 07-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discretelimit, organization={Wolfram Research}, title={DiscreteLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteLimit.html}, note=[Accessed: 07-November-2024 ]}