DiscreteLimit[f,k∞]
给出序列 f[k] 当 k 趋近于无穷大的整数时的极限 k∞f(k).
DiscreteLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
给出整数上的嵌套极限 ![]() ⋯
⋯ ![]() f(k1,…,kn).
f(k1,…,kn).
DiscreteLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
给出整数上的多变量极限 ![]() f(k1,…,kn).
f(k1,…,kn).






DiscreteLimit
DiscreteLimit[f,k∞]
给出序列 f[k] 当 k 趋近于无穷大的整数时的极限 k∞f(k).
DiscreteLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
给出整数上的嵌套极限 ![]() ⋯
⋯ ![]() f(k1,…,kn).
f(k1,…,kn).
DiscreteLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
给出整数上的多变量极限 ![]() f(k1,…,kn).
f(k1,…,kn).
更多信息和选项


- DiscreteLimit 亦称为离散极限或整数上的极限.
- DiscreteLimit 计算序列 f 当变量 k 或 ki 变得任意大时的极限值.
- 可用
 f 来输入 DiscreteLimit[f,k∞]. 可用
f 来输入 DiscreteLimit[f,k∞]. 可用  dlim
dlim 来输入模板
来输入模板 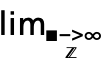 ,用
,用  把光标从底部移动到主体.
把光标从底部移动到主体. - 可用
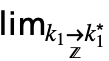 …
…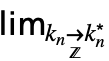 f 来输入 DiscreteLimit[f,{k1,…,kn}{
f 来输入 DiscreteLimit[f,{k1,…,kn}{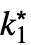 ,…,
,…,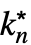 }].
}]. 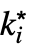 的极限值为 ±∞.
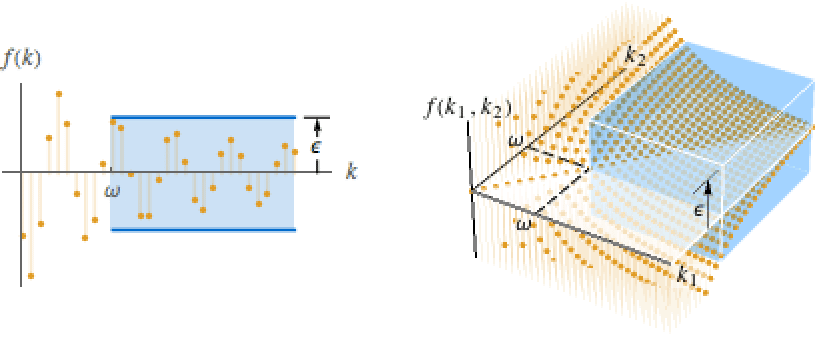
的极限值为 ±∞. - 对于有限值 f*:
-
DiscreteLimit[f,k∞]f* 对于每一个 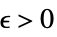 ,有一个
,有一个 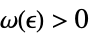 ,使得
,使得 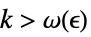 实质蕴涵
实质蕴涵 ![TemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon TemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon](Files/DiscreteLimit.zh/27.png)
DiscreteLimit[f,{k1,…,kn}{∞,…,∞}]f* 对于每一个 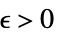 ,有一个
,有一个 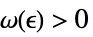 ,使得
,使得 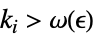 实质蕴涵
实质蕴涵 ![TemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon TemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon](Files/DiscreteLimit.zh/31.png)
- DiscreteLimit[f[k],k-∞] 等价于 DiscreteLimit[f[-l],l∞] 等.
- 当可以证明极限不存在时,DiscreteLimit 返回 Indeterminate,如果无法找到极限,则不进行计算,直接返回.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 GenerateConditions Automatic 是否为参数生成条件 Method Automatic 所用的方法 PerformanceGoal "Quality" 优化的目标 - GenerateConditions 的可能设置包括:
-
Automatic 只汇报非通用条件 True 汇报所有条件 False 不汇报条件 None 如果需要条件,则不进行计算,直接返回 - PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 如果设置为 "Quality", DiscreteLimit 通常能求解更多问题或产生更简单的结果,但会需要更多时间和内存.
范例
打开所有单元 关闭所有单元基本范例 (4)
范围 (37)
整数函数序列 (5)
分段函数序列 (3)
数论函数序列 (4)
形式序列 (6)
计算涉及 Inactive 和的序列的极限:
Inactive 和的嵌套极限:
交换 DiscreteLimit 和 Sum 的顺序,分两步计算,获得同样的结果:
涉及 Inactive 积的序列的极限:
Inactive 积的嵌套极限:
交换 DiscreteLimit 和 Product 的顺序,分两步计算,获得同样的结果:
涉及 Inactive 连分数的序列的极限:
Inactive 连分数的嵌套极限:
通过运用 DiscreteLimit 和 ContinuedFractionK,分两步计算,获得同样的结果:
选项 (6)
GenerateConditions (3)
当设置为 GenerateConditions->True 时,即便是非通用条件,也会汇报:
Method (1)
PerformanceGoal (1)
应用 (35)
几何极限 (3)
和与积 (6)
用 Sum 获得同样的答案:
用 Sum 直接计算结果:
用 SumConvergence 和 Sum 确认级数是发散的:
用 Regularization 获取级数的阿贝尔和:
用 Sum 直接获取同样的答案:
用 Product 获取同样的答案:
级数收敛 (4)
计算该级数的 DiscreteRatio:
用 SumConvergence 验证结果:
用 SumConvergence 验证结果:
用 Raabe 检验法来检验一般项由下式给出的级数的收敛性:
Raabe 检验法在此是适用的,因为比例检验法的结果不确定:
用 SumConvergence 验证结果:
用 SumConvergence 验证结果:
经典定义 (3)
用 Reduce 显示对于所有的 n>=12,定义成立:
用 DiscretePlot 验证结果:
证明下列序列发散于 Infinity,并用 M=35 检验经典定义:
用 Reduce 显示对于所有的 n >= 10,定义成立:
用 DiscretePlot 验证结果:
递归序列 (3)
数学常数 (5)
数学函数 (2)
Stolz–Cesàro 定理 (2)
Stolz–Cesàro 定理是 L'Hôpital 规则的离散版本,在合适的条件下可用于计算序列之比的极限. 该定理指出:
用 DiscreteLimit 直接获取同样的结果:
用 DiscreteLimit 直接获取同样的结果:
计算复杂性 (3)
均匀收敛 (2)
其它应用 (2)
用 InverseLaplaceTransform 获取同样的结果:
随机变量序列的概率分布的极限(如果存在)称为渐进分布. 用二项式分布序列的渐进分布获得泊松分布,其中均值 λ、概率和试验次数的乘积保持不变:
验证这是 PoissonDistribution 的 PDF:
属性和关系 (15)
如果 f 和 g 的极限为有限值,则 DiscreteLimit 在和上满足分配律:
如果 f 和 g 的极限为有限值,则 DiscreteLimit 在乘积上满足分配律:
Stolz–Cesàro 规则可被原来求两个序列的比的极限:
如果 Limit 存在,则 DiscreteLimit 也存在,且它们的值相同:
如果 DiscreteLimit 存在,则 DiscreteMaxLimit 也存在,且它们的值相同:
如果 DiscreteLimit 存在,则 DiscreteMinLimit也存在,且它们的值相同:
序列的极限通过终值定理与其 ZTransform 相关:
参见
Limit DiscreteMaxLimit DiscreteMinLimit SumConvergence RSolveValue AsymptoticRSolveValue AsymptoticSum
Function Repository: RichardsonExtrapolate
文本
Wolfram Research (2017),DiscreteLimit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLimit.html.
CMS
Wolfram 语言. 2017. "DiscreteLimit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteLimit.html.
APA
Wolfram 语言. (2017). DiscreteLimit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteLimit.html 年
BibTeX
@misc{reference.wolfram_2025_discretelimit, author="Wolfram Research", title="{DiscreteLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLimit.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretelimit, organization={Wolfram Research}, title={DiscreteLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteLimit.html}, note=[Accessed: 27-February-2026]}