EstimatedDistribution
EstimatedDistribution[data,dist]
估计 data 的参数分布 dist.
EstimatedDistribution[data,dist,{{p,p0},{q,q0},…}]
估计参数 p、q、…,起始值为 p0、q0、….
EstimatedDistribution[data,dist,idist]
估计分布 dist,其中起始值选自于实体化分布 idist.
更多信息和选项

- EstimatedDistribution 返回分布 dist,其中对于任何非数值型值将插入参数估计.
- data 必须是给定分布 dist 的所有可能结果的列表.
- 分布 dist 可为具有未知参数的任意参数型单变量、多变量或导出分布.
- 可以给定下列选项:
-
AccuracyGoal Automatic 要达到的准确度 ParameterEstimator "MaximumLikelihood" 应该使用何种参数估计量 PrecisionGoal Automatic 要达到的精度 WorkingPrecision Automatic 内部计算所用的精度 - 下列基本设置可以用于 ParameterEstimator:
-
"MaximumLikelihood" 对数似然函数最大化 "MethodOfMoments" 原始矩匹配 "MethodOfCentralMoments" 中心矩匹配 "MethodOfCumulants" 累积量匹配 "MethodOfFactorialMoments" 阶乘矩匹配 - 最大似然估计试图使对数似然函数
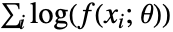 最大化,其中
最大化,其中 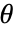 为分布参数,
为分布参数,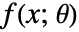 是分布的概率密度函数.
是分布的概率密度函数. - 矩法求解
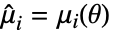 、
、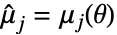 、
、 ,其中
,其中 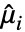 为分布的第
为分布的第 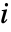
 阶样本矩,
阶样本矩,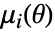 为分布的第
为分布的第 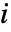
 阶矩,分布的参数为
阶矩,分布的参数为 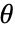 .
. - 基于矩法的估计量不一定满足参数的所有限制条件.
范例
打开所有单元关闭所有单元范围 (15)
基本用途 (5)
选项 (4)
ParameterEstimator (3)
利用 FindMaximum 得到估计量:
利用 EvaluationMonitor 提取所采样的点:
应用 (14)
文本频率 (1)
地震幅度 (1)
EstimatedDistribution 可以与诸如 MixtureDistribution 的结构体一起使用,以创建多态模型:
从一个 NormalDistribution 与另一个的可能混合进行分布拟合:
风速分析 (1)
对数据进行 RayleighDistribution 拟合:
机动车辆的汽油使用效率 (1)
地震间隔时间 (1)
数据包含从1902年12月16日至1977年3月4日,在世界范围内的大地震(震级至少7.5或者超过1000人死亡)的等待时间(以天数为单位):
通过 ExponentialDistribution 对等待时间进行建模:
地震频率 (1)
喷泉喷发的时间间隔 (1)
Old Faithful 泉喷发的等待时间的直方图呈现出两种模式:
对数据进行 MixtureDistribution 拟合:
水流速率 (1)
把年平均最小日流量作为 MinStableDistribution 建模:
属性和关系 (8)
EstimatedDistribution 给出插入参数估计的分布:
FindDistributionParameters 把参数估计作为替换规则给出:
EstimatedProcess 估计参数过程
EstimatedDistribution 估计参数分布:
使用 DistributionFitTest 测试拟合质量:
EstimatedDistribution 在一个参数分布中估计参数:
SmoothKernelDistribution 给出一个非参数化的内核密度估计:
使用 SmoothHistogram 可视化非参数密度:
EstimatedDistribution 给出参数的最大似然估计:
使用 Likelihood 计算似然值:
使用 LogLikelihood 计算对数似然值:
使用 Moment 从数据计算原始矩:
使用 QuantilePlot 可视化实际分位数比拟合分布分位数:
当估计在 QuantilePlot 中实现时,获取同样的可视化:
EstimatedDistribution 忽略 TimeSeries 和 EventSeries 中的时间戳:
对于 TemporalData,忽略所有路径结构:
文本
Wolfram Research (2010),EstimatedDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/EstimatedDistribution.html.
CMS
Wolfram 语言. 2010. "EstimatedDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedDistribution.html.
APA
Wolfram 语言. (2010). EstimatedDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EstimatedDistribution.html 年