EstimatedDistribution

EstimatedDistribution[data,dist]

estimates the parametric distribution dist from data.

EstimatedDistribution[data,dist,{{p,p0},{q,q0},…}]

estimates the parameters p, q, … with starting values p0, q0, ….

EstimatedDistribution[data,dist,idist]

estimates distribution dist with starting values taken from the instantiated distribution idist.

Details and Options

  • EstimatedDistribution returns the distribution dist with parameter estimates inserted for any non-numeric values.
  • The data must be a list of possible outcomes from the given distribution dist.
  • The distribution dist can be any parametric univariate, multivariate, or derived distribution with unknown parameters.
  • The following options can be given:
  • AccuracyGoalAutomaticthe accuracy sought
    ParameterEstimator "MaximumLikelihood"what parameter estimator to use
    PrecisionGoalAutomaticthe precision sought
    WorkingPrecision Automaticthe precision used in internal computations
  • The following basic settings can be used for ParameterEstimator:
  • "MaximumLikelihood"maximize the log‐likelihood function
    "MethodOfMoments"match raw moments
    "MethodOfCentralMoments"match central moments
    "MethodOfCumulants"match cumulants
    "MethodOfFactorialMoments"match factorial moments
  • The maximum likelihood method attempts to maximize the log-likelihood function 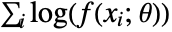, where 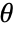are the distribution parameters and 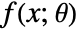is the PDF of the distribution.
  • The method of moments solves 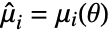, , 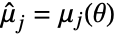, where 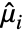is the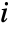 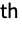^(th) sample moment and 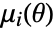is the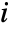 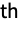^(th) moment of the distribution, with parameters .
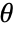  • Method-of-moment-based estimators may not satisfy all restrictions on parameters.

Examples

open allclose all

Basic Examples  (3)

Obtain the maximum likelihood parameter estimates, assuming a gamma distribution:

Visually compare the PDFs for the original and estimated distributions:

Obtain the method of moments estimates:

Estimate parameters for a multivariate distribution:

Estimated parameters from data with quantities:

Scope  (15)

Basic Uses  (5)

Estimate both parameters for a binomial distribution:

Estimate p, assuming n is known:

Estimate n, assuming p is known:

Get the distribution with maximum likelihood parameter estimate for a particular family:

Check goodness of fit by comparing a histogram of the data and the estimate's PDF:

Perform goodness-of-fit tests with null distribution dist:

Perform tests correcting for estimation of the parameter:

Estimate parameters by maximizing the log‐likelihood:

Plot the log‐likelihood function to visually check that the solution is optimal:

Visualize a log‐likelihood surface to find rough values for the parameters:

Supply those rough values as starting values for the estimation:

Estimate the normal approximation of Poisson data:

Obtain the estimate to 20 digits:

Univariate Parametric Distributions  (2)

Estimate parameters for a continuous distribution:

Compare empirical and distribution quantiles:

Estimate parameters for a discrete distribution:

Multivariate Parametric Distributions  (2)

Estimate parameters for a discrete multivariate distribution:

Estimate parameters for a continuous multivariate distribution:

Compare the difference between the original and estimated PDFs:

Derived Distributions  (6)

Estimate parameters for a truncated normal:

Compare original and estimated distribution:

Estimate parameters for a constructed distribution:

Estimate parameters for a product distribution:

Estimate parameters for a copula distribution:

Compare original and estimated CDFs:

Estimate parameters for a component mixture:

Estimate the mixture probabilities assuming the component distributions are known:

Estimate parameters for quantity distribution in specified units:

Options  (4)

ParameterEstimator  (3)

Estimate parameters by matching central moments:

Other moment‐based methods typically give similar results:

Estimate parameters based on default moments:

Estimate parameters from the first and fourth moments:

Obtain the maximum likelihood estimates using the default method:

Use FindMaximum to obtain the estimates:

Use EvaluationMonitor to extract the points sampled:

Visualize the sequences of sampled and values:

WorkingPrecision  (1)

Use machine precision for continuous parameters by default:

Obtain a higher-precision result:

Applications  (14)

Estimation of Similarly Shaped Distributions  (1)

Model lognormal distributed data with a gamma distribution:

Compare the distributions of the simulation and estimated distributions:

Accident Claims  (1)

The number of accident claims per policy per year from an insurance company:

Model the data by a logarithmic series distribution since most policies have at most one claim:

Word Lengths in Different Languages  (1)

Get word length data for several languages:

Model the word lengths for each language as binomially distributed:

Compare the actual and estimated distributions:

Text Frequency  (1)

The word count in a text follows a Zipf distribution:

Fit a ZipfDistribution to the word frequency data:

Compare the frequency histogram with the estimated distribution:

Earthquake Magnitudes  (1)

EstimatedDistribution can be used with constructs like MixtureDistribution to create multimodal models:

The magnitudes of earthquakes in the United States in the selected years have two modes:

Fit distribution from possible mixtures of one NormalDistribution with another:

Compare the histogram to the PDF of the estimated distribution:

Find the probability of an earthquake of magnitude 7 or higher:

Find the mean earthquake magnitude:

Simulate magnitudes of the next 30 earthquakes:

Wind Speed Analysis  (1)

Model monthly maximum wind speeds in Boston:

Fit the data to a RayleighDistribution:

An ExtremeValueDistribution:

Compare the empirical quantiles and those for the fitted distributions to see where the models deviate from the data:

Distribution of Incomes  (1)

Model incomes at a large state university:

Assume the salaries are Dagum distributed:

Assume they follow a more general Pareto distribution:

Compare the subtle differences in the estimated distributions:

Automobile Fuel Efficiency  (1)

The average city and highway mileage for midsize cars follows a binormal distribution:

Assume city and highway miles per gallon are normally distributed and correlated:

Show the distribution of city and highway mileage:

Visualize the joint density with contours on a logarithmic scale:

Earthquake Waiting Times  (1)

The data contains waiting times in days between serious (magnitude at least 7.5 or over 1000 fatalities) earthquakes worldwide, recorded from 12/16/1902 to 3/4/1977:

Model waiting times by an ExponentialDistribution:

Estimate the average and median number of days between major earthquakes:

Earthquake Frequency  (1)

The number of earthquakes per year can be modeled by SinghMaddalaDistribution:

Fit the distribution to the data:

Compare the data histogram with the PDF of the estimated distribution:

Find the probability of at least 60 earthquakes in the US in a year:

Time between Geyser Eruptions  (1)

Mixtures can be used to model multimodal data:

A histogram of waiting times for eruptions of the Old Faithful geyser exhibits two modes:

Fit a MixtureDistribution to the data:

Compare the histogram to the PDF of the estimated distribution:

Find the probability that the waiting time is over 80 minutes:

Simulate waiting times for the next 60 eruptions:

Stock Price Distribution  (1)

Lognormal distribution can be used to model stock prices:

Fit the distribution to the data:

Observe that the quantiles for the data and distribution match well except for the largest values:

Water Flow Rates  (1)

Consider the annual minimum daily flows given in cubic meters per second for the Mahanadi river:

Model the annual minimum mean daily flows as a MinStableDistribution:

Compare the histogram of the data to the PDF of the estimated distribution:

Simulate annual minimum mean daily flows for the next 30 years:

Population Sizes  (1)

Use a Pareto distribution to model Australian city population sizes:

Estimate the probability that a city has a population of at least 10,000 people:

Compute the probability based on the original data:

Properties & Relations  (8)

EstimatedDistribution gives a distribution with parameter estimates inserted:

FindDistributionParameters gives parameter estimates as replacement rules:

EstimatedProcess estimates a parametric process:

EstimatedDistribution estimates a parametric distribution:

Estimate distribution parameters by maximum likelihood:

Use DistributionFitTest to test the quality of the fit:

Extract the fitted distribution:

Obtain a table of relevant test statistics and ‐values:

EstimatedDistribution estimates parameters in a parametric distribution:

SmoothKernelDistribution gives a nonparametric kernel density estimate:

Compare the PDFs for the nonparametric and parametric distributions:

Visualize the nonparametric density using SmoothHistogram:

EstimatedDistribution gives a maximum likelihood estimate of parameters:

Compute the likelihood using Likelihood:

Compute the log‐likelihood using LogLikelihood:

Estimate parameters by matching raw moments:

Compute raw moments from the data using Moment:

Compute the same moments from the estimated distribution:

Estimate parameters for a Weibull distribution:

Use QuantilePlot to visualize empirical quantiles versus fitted distribution quantiles:

Obtain the same visualization when the estimation is done within QuantilePlot:

EstimatedDistribution ignores time stamps in TimeSeries and EventSeries:

The same as:

For TemporalData, all the path structure is ignored:

The same as:

Possible Issues  (3)

Solutions of method of moment equations can give parameters that are not valid:

For a continuous distribution:

Good starting values may be needed to obtain a good solution:

Good starting values may also result in quicker results:

Wolfram Research (2010), EstimatedDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/EstimatedDistribution.html.

Text

Wolfram Research (2010), EstimatedDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/EstimatedDistribution.html.

CMS

Wolfram Language. 2010. "EstimatedDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedDistribution.html.

APA

Wolfram Language. (2010). EstimatedDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatedDistribution.html

BibTeX

@misc{reference.wolfram_2024_estimateddistribution, author="Wolfram Research", title="{EstimatedDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatedDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_estimateddistribution, organization={Wolfram Research}, title={EstimatedDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/EstimatedDistribution.html}, note=[Accessed: 21-November-2024 ]}