Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

LerchPhi

LerchPhi

LerchPhi[z,s,a]

gives the Lerch transcendent .

Details and Options

Mathematical function, suitable for both symbolic and numerical manipulation.
LerchPhi is a generalization of Zeta[s], Zeta[s,a], PolyLog and related functions. »
For 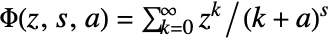, the Lerch transcendent is defined by $TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/((k+a)^s)$ .
For 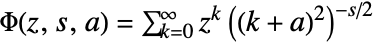, the definition used is $TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/(((k+a)^2)^(s/2))$ , where by default any term with 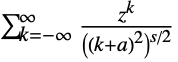is excluded.
LerchPhi is identical to HurwitzLerchPhi for . »
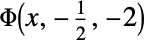LerchPhi follows the branch cut conventions of the generalized Riemann 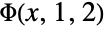function as given by Zeta. By contrast, HurwitzLerchPhi uses the branch cuts as defined by HurwitzZeta. »
Unlike HurwitzLerchPhi, LerchPhi by default has regularized, finite values when the defining series has terms with zero denominator. »
LerchPhi takes the following options:

	DoublyInfinite	False	whether to compute the transcendent defined by a doubly inifinite sum
	IncludeSingularTerm	False	whether to include terms for which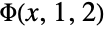

LerchPhi[z,s,a,DoublyInfinite->True] gives the sum .
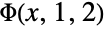The option IncludeSingularTermFalse only affects values at and . »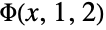
For certain special arguments, LerchPhi automatically evaluates to exact values.
LerchPhi can be evaluated to arbitrary numerical precision.
LerchPhi automatically threads over lists.
LerchPhi can be used with Interval and CenteredInterval objects. »

Examples

open all close all

Basic Examples (6)

Evaluate numerically:

Simple exact values are generated automatically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Scope (32)

Numerical Evaluation (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number input:

Evaluate efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix LerchPhi function using MatrixFunction:

Specific Values (6)

Simple exact values are generated automatically:

is a rational function in and a polynomial in if :

The following is manifestly a rational function in :

It is also a polynomial in :

LerchPhi[z,s,0] is simply PolyLog[s,z]:

LerchPhi[z,s,1] is PolyLog[s,z]/z:

LerchPhi[-1,s,a] gives expressions in Zeta:

Value at the origin:

Approaching along the line gives the same result:

Approaching along the line gives :

Approaching the origin along the line also gives 1, but in a more interesting fashion:

Find a value of z for which LerchPhi[z,1,0]=1.05:

Visualization (3)

Plot the LerchPhi function:

Plot the real part of the LerchPhi function:

Plot the imaginary part of the LerchPhi function:

Visualize the dependence on :

Visualize how LerchPhi and HurwitzLerchPhi agree for but not :

Function Properties (11)

Real domain of LerchPhi:

Complex domain:

Approximate function range of :

LerchPhi threads elementwise over lists and matrices:

is not an analytic function:

Nor is it meromorphic:

is neither non-decreasing nor non-increasing:

is injective:

is not surjective:

is neither non-negative nor non-positive:

has both singularity and discontinuity for or for :

is neither convex nor concave:

TraditionalForm formatting:

Differentiation (2)

First derivative with respect to z:

First derivative with respect to a:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z when s=2 and a=1/3:

Series Expansions (4)

Find the Taylor expansion in for generic and using Series:

Plots of the first three approximations around :

Series expansion in at a generic point:

Series expansion about when has the singular value and :

Do the expansion about instead:

Series expansion in near , , :

Series expansion in about the same point:

LerchPhi can be applied to power series:

Options (5)

DoublyInfinite (3)

By default, LerchPhi includes only terms with positive :

In a symmetric case, setting DoublyInfinite->True just doubles the result:

In a more general case, negative terms have a more complicated effect:

IncludeSingularTerm (2)

LerchPhi by default gives regularized, finite values for for :

Obtain the raw, infinite value by setting IncludeSingularTerm->True:

For noninteger , the option does not change the value:

Nor does it have any effect when :

LerchPhi[z,s,a,IncludeSingularTermTrue] is ComplexInfinity when there is a singular term and :

It is indeterminate if there is a singular term and :

Applications (2)

Find a zero of LerchPhi:

Central moments of a geometric probability distribution:

Explicit forms for small k:

Properties & Relations (10)

Obtain LerchPhi from sums:

LerchPhi is a numeric function:

LerchPhi[z,s,a] gives regularized, finite values when a:

Values near are very large:

HurwitzLerchPhi agrees with LerchPhi for :

This is not true for :

LerchPhi by default omits singular terms for which the denominator is zero:

The term in the defining series is omitted:

HurwitzLerchPhi, by contrast, includes these terms:

Zeta[s] equals LerchPhi[1,s,1] for Re[s]>1:

Zeta[s,a] equals LerchPhi[1,s,a] for Re[s]>1:

HurwitzLerchPhi is different from LerchPhi in the choice of branch cuts:

HurwitzLerchPhi matches HurwitzZeta, while LerchPhi matches Zeta:

LerchPhi is a generalization of PolyLog:

DirichletEta is a special case of LerchPhi:

DirichletBeta is dilation of LerchPhi:

Possible Issues (4)

A larger setting for $MaxExtraPrecision can be needed:

LerchPhi uses numerical comparisons when singular terms are included:

For , LerchPhi cannot always be evaluated in terms of Zeta for symbolic s:

For , they agree:

But this is not true for :

The line is not considered to have a singular term:

This is consistent with Sum, which considers to be for all :

Top